Carbon
| |||||||||||||||||||||||||
| General | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name, Symbol, Number | carbon, C, 6 | ||||||||||||||||||||||||
| Chemical series | nonmetals | ||||||||||||||||||||||||
| Group, Period, Block | 14, 2, p | ||||||||||||||||||||||||
| Appearance | black (graphite) colorless (diamond) 
| ||||||||||||||||||||||||
| Atomic mass | 12.0107(8) g/mol | ||||||||||||||||||||||||
| Electron configuration | 1s2 2s2 2p2 | ||||||||||||||||||||||||
| Electrons per shell | 2, 4 | ||||||||||||||||||||||||
| Physical properties | |||||||||||||||||||||||||
| Phase | solid | ||||||||||||||||||||||||
| Density (near r.t.) | (graphite) 2.267 g/cmÂł | ||||||||||||||||||||||||
| Density (near r.t.) | (diamond) 3.513 g/cmÂł | ||||||||||||||||||||||||
| Melting point | ? triple point, ca. 10 MPa and (4300â4700) K (? °C, ? °F) | ||||||||||||||||||||||||
| Boiling point | subl. ? ca. 4000 K (? °C, ? °F) | ||||||||||||||||||||||||
| Heat of fusion | (graphite)Â ? 100 kJ/mol | ||||||||||||||||||||||||
| Heat of fusion | (diamond)Â ? 120 kJ/mol | ||||||||||||||||||||||||
| Heat of vaporization | ? 355.8 kJ/mol | ||||||||||||||||||||||||
| Heat capacity | (25 °C) (graphite) 8.517 J/(mol¡K) | ||||||||||||||||||||||||
| Heat capacity | (25 °C) (diamond) 6.115 J/(mol¡K) | ||||||||||||||||||||||||
| |||||||||||||||||||||||||
| Atomic properties | |||||||||||||||||||||||||
| Crystal structure | hexagonal | ||||||||||||||||||||||||
| Oxidation states | 4, 2 (mildly acidic oxide) | ||||||||||||||||||||||||
| Electronegativity | 2.55 (Pauling scale) | ||||||||||||||||||||||||
| Ionization energies (more) |
1st: 1086.5 kJ/mol | ||||||||||||||||||||||||
| 2nd: 2352.6 kJ/mol | |||||||||||||||||||||||||
| 3rd: 4620.5 kJ/mol | |||||||||||||||||||||||||
| Atomic radius | 70 pm | ||||||||||||||||||||||||
| Atomic radius (calc.) | 67 pm | ||||||||||||||||||||||||
| Covalent radius | 77 pm | ||||||||||||||||||||||||
| Van der Waals radius | 170 pm | ||||||||||||||||||||||||
| Miscellaneous | |||||||||||||||||||||||||
| Magnetic ordering | diamagnetic | ||||||||||||||||||||||||
| Thermal conductivity | (300 K) (graphite) (119â165) W/(m¡K) | ||||||||||||||||||||||||
| Thermal conductivity | (300 K) (diamond) (900â2320) W/(m¡K) | ||||||||||||||||||||||||
| Thermal diffusivity | (300 K) (diamond) (503â1300) mm²/s | ||||||||||||||||||||||||
| Mohs hardness | (graphite) 0.5 | ||||||||||||||||||||||||
| Mohs hardness | (diamond) 10.0 | ||||||||||||||||||||||||
| CAS registry number | 7440-44-0 | ||||||||||||||||||||||||
| Notable isotopes | |||||||||||||||||||||||||
| |||||||||||||||||||||||||
Carbon (chemical symbol C; atomic number 6) is a remarkable chemical element that plays a vital role in the structures and processes of the living and nonliving worlds. Without it, our physical existence and that of other organisms would not be possible. Its different forms include graphite, one of the softest substances, and diamond, the hardest naturally occurring material. Carbon is known to be part of a huge variety of compounds, including some that occur in the Sun, stars, and planetary atmospheres. We use carbon compounds for fuel and the synthesis of a wide range of materials such as plastics, paints, textiles, and pharmaceuticals. Researchers are now investigating the uses of new forms of carbon, known as fullerenes, leading to the developing field of nanotechnology.
The careless disposal of paints, plastics, and other carbon-containing materials has polluted the environment, and the misuse of drugs has caused needless suffering and pain. Such practices are symptomatic of an inadequate understanding of the values and principles of the natural world. While efforts are now being made to clean up the environment and combat drug abuse, humanity needs to restore its sense of values as well, to prevent these problems from recurring.
Occurrence
Carbon is an abundant nonmetal that has been known since prehistory. Early peoples produced it in the form of charcoal by burning organic material (such as wood) in insufficient oxygen.
The name carbon comes from the French word charbone, which in turn is derived from the Latin carbo, meaning charcoal. In German and Dutch, the names for carbon are Kohlenstoff and koolstof, respectively, both of which literally mean "coal-stuff."
Pure carbon can occur in a variety of forms known as allotropes, such as graphite and diamond. In addition, carbon can bind to itself and various other elements to form compounds.
On Earth, carbon and its compounds are widely dispersed in the air, water, and land. They are also present in the Sun and stars, and it is thought that carbon atoms were first formed by nuclear reactionsâparticularly, the collision of three alpha particles (helium nuclei)âin the interior of stars. Moreover, carbon is found in comets and in the atmospheres of most planets in the solar system. Some meteorites contain microscopic diamonds that may have been created when the solar system was in its formative stages.
In the United States, graphite is found in large quantities in New York and Texas. It is also abundant in Russia, Mexico, Greenland, and India.
Natural diamonds occur in the mineral kimberlite found in ancient volcanic necks or pipes. Most diamond deposits are in Africa, notably in South Africa, Namibia, Botswana, the Republic of the Congo and Sierra Leone. Other deposits have been found in Arkansas, Canada, the Russian Arctic, Brazil, and Northern and Western Australia.
Additional allotropic forms of carbon, classified as fullerenes, were discovered as byproducts of molecular beam experiments in the 1980s.
Notable characteristics
The chemical symbol for carbon is C, and its atomic number (the number of protons in the nucleus of each atom) is 6. Each carbon atom is capable of forming strong chemical bonds, called covalent bonds, with up to four other atoms. Carbon is therefore said to be tetravalent.
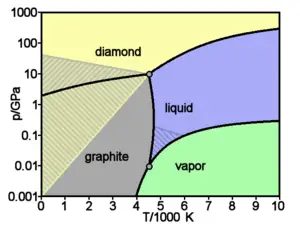
Carbon has the highest melting/sublimation point of all elements. If heated at atmospheric pressure, carbon does not melt but sublimates (the solid form vaporizes) above 4000 K. Thus, carbon remains a solid at higher temperatures than metals with the highest melting points, including tungsten and rhenium.
Carbon that has exceptionally high surface area is known as activated carbon or activated charcoal. It is produced by treating charcoal (or other carbon-rich materials) with certain acids or gases at high temperature. It can adsorb (absorb on its surface) various materials, and is therefore useful for removing pollutants from water and air.
Isotopes
Carbon has two stable, naturally occurring isotopes: carbon-12 (12C) and carbon-13 (13C), at relative abundances of approximately 98.9 percent and 1.1 percent, respectively. In 1961, the International Union of Pure and Applied Chemistry adopted the isotope carbon-12 as the basis for atomic weights.
One naturally occurring radioisotope, carbon-14 (14C), has a half-life of about 5,730 years. Twelve other radioisotopes have been produced artificially. Of these, the shortest lived is 8C, which has a half-life of about 1.987x10-21 seconds.
Allotropes
Carbon can exist in different structural states known as allotropes. Two well-known allotropes are graphite, one of the softest substances, and diamond, the hardest naturally occurring mineral.
Graphite has a crystalline structure in which the carbon atoms are arranged in layers of flat sheets. Each sheet consists of a network of hexagonal (six-membered) rings in which each carbon atom is bonded to three other atoms. While each sheet is exceptionally stable, it interacts loosely with adjacent sheets so that they can readily slide past one another.
Diamond, which is formed in the Earth at very high pressures, adopts a different crystalline structure. Each carbon atom is bonded to four others, which together form a tetrahedral shape surrounding the central carbon. The overall structure is a three-dimensional network of puckered six-membered rings of carbon atoms. In this manner, each diamond crystal regardless of size can be thought of as a single molecule of carbon atoms. At room temperature, a diamond crystal undergoes an extremely slow transition to graphite.
Diamond and graphite have certain diametrically opposite features. Diamond is transparent and hard; it acts as an excellent electrical insulator, and can be used as an abrasive. By contrast, graphite is opaque and soft. It conducts electricity, and is a good lubricant. Diamond crystallizes in the cubic system but graphite crystallizes in the hexagonal system.
Carbon that lacks an overall crystalline structure is known as amorphous carbon. Although it is possible to produce carbon that is entirely amorphous (non-crystalline), material that is described as amorphous usually includes small crystals of graphite or diamond. Amorphous carbon is the main constituent of charcoal, soot (lampblack or carbon black), and activated carbon.
In addition, several exotic allotropes have been synthesized or discovered, including fullerenes, carbon nanotubes, lonsdaleite, carbon nanofoam, and aggregated diamond nanorods. The carbon atoms in these allotropes have different structural arrangements.
A fullerene is composed of a sheet of carbon atoms linked together in hexagonal and pentagonal rings to take the overall form of a hollow sphere or ellipsoid. A spherical fullerene is also called a buckyball. The most well-known buckyball is Buckminsterfullerene (containing 60 carbon atoms per sphere), named after Richard Buckminster Fuller, the architect who developed the geodesic dome.
A carbon nanotube likewise consists of a sheet of carbon atoms linked in hexagonal and pentagonal rings, but the overall shape is that of a hollow cylinder. Sometimes called a buckytube, it is classified as part of the fullerene family of carbon compounds.
Lonsdaleite is thought to form when meteoric graphite falls to Earth. The impact's heat and stress transform the graphite into a structure similar to diamond, but graphite's hexagonal crystal lattice is retained. Also known as hexagonal diamond, lonsdaleite is transparent and brownish yellow in color.
Carbon nanofoam was unexpectedly produced by scientists in Australia in 1997*. It consists of low-density clusters of carbon atoms that are bonded in six- and seven-membered rings. Surprisingly, the material is attracted to magnets and can be magnetized at temperatures below -183°C.
Aggregated diamond nanorods (ADNRs) are denser and harder than diamond, and they appear to be the least compressible material known to humankind. They were produced in 2005* by physicists in Germany who compressed carbon-60 molecules under a pressure of 20 GPa while heating the material to 2500 K.
Compounds of carbon
Each carbon atom can form covalent bonds with other carbon atoms and various other elementsâmost commonly with hydrogen, oxygen, nitrogen, and chlorine. By doing so, carbon forms stable compounds that consist of linear and branched chains and ring-shaped molecules.
Scientists are aware of nearly 10 million carbon compounds, and new ones are synthesized regularly. Carbon compounds constitute the vast majority of all known chemical compounds. Most compounds of carbon are classified as organic compounds, which form the basis for the field of organic chemistry.
When combined with only hydrogen, carbon forms a variety of hydrocarbons, including methane, propane, butane, benzene, and naphthalene. Natural sources of hydrocarbons are coal, petroleum, and natural gas.
When bound to oxygen alone, carbon forms carbon dioxide (CO2), carbon monoxide (CO), and the uncommon carbon suboxide, C3O2. Carbon dioxide in the Earth's atmosphere is essential for plants to perform photosynthesis, and, as a greenhouse gas, it helps retain heat from the Sun and keep our planet warm enough to sustain life. Carbon monoxide is a colorless, odorless, and highly poisonous gas formed by incomplete combustion.
When attached to both oxygen and hydrogen, carbon forms various types of compounds, including those classified as alcohols, esters, aldehydes, ketones, and carboxylic acids.
Thousands of carbon compoundsâincluding carbohydrates, fats, proteins, and nucleic acidsâare produced in and used by living systems. Other compoundsâparticularly the carbonates of metals such as calcium, magnesium, and ironâare major components of rocks, including limestone, dolomite, and marble.
In exceptional cases, carbon takes the form of an anion. With reactive metals such as tungsten, carbon forms either carbides (C-) or acetylides (C22-) to form materials with very high melting points. On the other hand, some carbides, such as carborundum (SiC), are lattices held together by covalent bonds.
Applications
Carbon and its compounds play significant roles in both natural and artificial systems. The structures and functions of all known living organisms are vitally dependent on carbon compounds. Some of the human uses of carbon and its compounds are listed below.
- Diamonds, being rare and attractive, have long been used in jewelry. Given their extreme hardness, they are also useful for drill bits and other industrial applications.
- Graphite is combined with clays to form the 'lead' used in pencils.
- In the porous, caked form known as charcoal, carbon is used for cooking and artwork.
- Carbon is added to iron to make steel.
- Carbon is used as a neutron moderator in nuclear reactors.
- Activated carbon is used in removing pollutants from the air and water streams, both in nature and in industrial processes. It is also used in medicine to absorb toxins or poisons from the digestive system.
- The isotope carbon-14 is used extensively for radioactive dating of carbon-containing materials.
- Fullerenes and carbon nanotubes have many potential uses in the nascent field of nanotechnology. Nanoparticles, however, might be toxic.
- Natural gas and petroleum (or crude oil), composed mainly of hydrocarbons, are important sources of fuel.
- Various materials derived from petroleum are used in synthesizing new substances such as plastics.
Precautions
Carbon and its compounds are usually safe materials, but there are some exceptions. For instance, inhalation of fine soot in large quantities can be dangerous. Also, carbon may catch fire at very high temperatures and burn vigorously. Some carbon compounds, such as carbon monoxide and cyanides (CN-), are lethally poisonous.
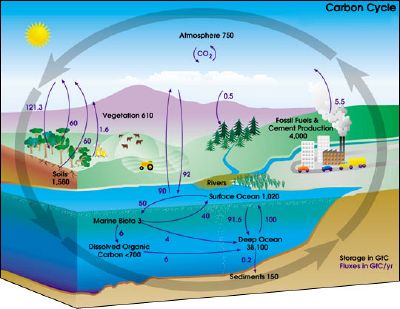
Carbon cycle
The paths that carbon follows in the environment are collectively called the carbon cycle. It is usually thought of as the processes of exchange of carbon involving four reservoirs: the Earth's atmosphere, terrestrial biosphere (including freshwater systems), oceans, and sediments (including fossil fuels). The carbon exchanges between reservoirs are the result of various chemical, physical, geological, and biological processes.
The global carbon budget is the balance of exchanges (incomes and losses) of carbon between the carbon reservoirs or within one specific loop of the carbon cycle. The carbon budget of a reservoir can provide information, for example, about whether the reservoir is functioning as a source or sink for carbon dioxide.
Carbon exchange by non-biological processes
Several non-biological processes are involved in the exchange of carbon between reservoirs. Some of these processes are as follows.
- Deposits of limestone and marble are composed mainly of calcium carbonate. As these rocks are eroded by water (especially acidic water), the calcium carbonate is broken down to form, among other things, carbon dioxide and carbonic acid.
- When limestone is heated to produce cement and lime (calcium oxide), a substantial amount of carbon dioxide is generated.
- At the surface of the oceans near the poles, the water becomes cooler and dissolves carbon dioxide from the air.
- At the surface of the oceans, in areas where the water becomes warmer, dissolved carbon dioxide is released back into the atmosphere.
- Volcanic eruptions release various gases into the atmosphere, including water vapor, carbon dioxide, and sulfur dioxide.
- Burning fossil fuelsâsuch as coal, petroleum products, and natural gasâreleases carbon dioxide and carbon particles into the air.
Carbon exchange involving biological processes
Living organisms play an important role in the carbon cycle, as outlined below.
- Certain organisms, called autotrophs, produce organic compounds using carbon dioxide from the air or water in the presence of an external source of energy. Most often, the source of energy is solar radiation, and the process is called photosynthesis; but a small number of autotrophs exploit chemical energy sources, and the process is called chemosynthesis. The main autotrophs involved in the carbon cycle are trees on land and phytoplankton in the oceans.
- Many organisms, called heterotrophs, feed on other organisms or their parts (such as fruits). Examples of heterotrophs are animals that feed on plants and other animals. Other heterotrophs are fungi and bacteria, which take up dead organic material (detritus) for fermentation or decay processes.
- Most carbon leaves the terrestrial biosphere through respiration. In the presence of oxygen, aerobic respiration releases carbon dioxide; in the absence of oxygen, anaerobic respiration releases methane. These gases eventually make their way into the air or water.
- Carbon may also leave the terrestrial biosphere when dead organic matter (such as peat) becomes incorporated in the geosphere. In particular, animal shells (made of calcium carbonate) may eventually become limestone through the process of sedimentation.
See also
ReferencesISBN links support NWE through referral fees
- Chang, Raymond. 2006. Chemistry. 9th ed. New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 0073221031.
- Cotton, F. Albert, and Geoffrey Wilkinson. 1980. Advanced Inorganic Chemistry. 4th ed. New York, NY: Wiley. ISBN 0-471-02775-8.
- Greenwood, N.N., and A. Earnshaw. 1998. Chemistry of the Elements. 2nd ed. Oxford, U.K.; Burlington, MA: Butterworth-Heinemann, Elsevier Science. ISBN 0750633654. Online version available here. Retrieved August 11, 2007.
- Janzen, H. H. 2004. Carbon cycling in earth systemsâa soil science perspective. Agriculture, ecosystems and environment 104:399â417.
External links
All links retrieved November 25, 2023.
- WebElements.com â Carbon
- It's Elemental â Carbon
- NASA Earth Observatory site - describing the carbon cycle
- NOAA's Carbon Cycle Greenhouse Gases Group
| ||||||||
| General subfields within the Natural sciences |
|---|
| Astronomy | Biology | Chemistry | Earth science | Ecology | Physics |
| Biogeochemical cycles |
|---|
| Carbon cycle - Hydrogen cycle - Nitrogen cycle |
| Oxygen cycle - Phosphorus cycle - Sulfur cycle - Water cycle |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.