Sun

The Sun

Observation data
Mean distance from Earth	149.6×106 km (92.95×106 mi) (8.31 minutes at the speed of light)
Visual brightness (V)	-26.8m
Absolute magnitude	4.8m
Spectral classification	G2V
Orbital characteristics
Mean distance from Milky Way core	~2.5×1017 km (26,000-28,000 light-years)
Galactic period	2.25-2.50×108 a
Velocity	217 km/s orbit around the center of the Galaxy, 20km/s relative to average velocity of other stars in stellar neighborhood
Physical characteristics
Mean diameter	1.392×106 km (109 Earth diameters)
Circumference	4.373×106 km (342 Earth diameters)
Oblateness	9×10-6
Surface area	6.09×1012 km² (11,900 Earths)
Volume	1.41×1018 km³ (1,300,000 Earths)
Mass	1.9891×1030 kg (332,950 Earths)
Density	1.408 g/cm³
Surface gravity	273.95 m s-2 (27.9 g)
Escape velocity from the surface	617.54 km/s
Surface temperature	5780 K
Temperature of corona	5 MK
Core temperature	~13.6 MK
Luminosity (Lsol)	3.827×1026 W 3.9×1028 lm or 100 lm/W efficacy
Mean Intensity (Isol)	2.009×107 W m-2 sr-1
Rotation characteristics
Obliquity	7.25° (to the ecliptic) 67.23° (to the galactic plane)
Right ascension of North pole	286.13° (19 h 4 min 30 s)
Declination of North pole	+63.87° (63°52' North)
Rotation period at equator	25.3800 days (25 d 9 h 7 min 13 s)
Rotation velocity at equator	7174 km/h
Photospheric composition (by mass)
Hydrogen	73.46 %
Helium	24.85 %
Oxygen	0.77 %
Carbon	0.29 %
Iron	0.16 %
Neon	0.12 %
Nitrogen	0.09 %
Silicon	0.07 %
Magnesium	0.05 %
Sulphur	0.04 %

The Sun is the star at the center of the Earth's solar system. The Earth and other matter (including other planets, asteroids, comets, meteoroids, and dust) orbit the Sun, which by itself accounts for more than 99 percent of the solar system's mass. Energy from the Sun—in the form of insolation from sunlight—supports almost all life on Earth via photosynthesis, and drives the Earth's climate and weather.

About 74 percent of the Sun's mass is hydrogen, 25 percent is helium, and the rest is made up of trace quantities of heavier elements. The Sun is thought to be about 4.6 billion years old and about halfway through its main-sequence evolution. Within the Sun's core, nuclear fusion reactions take place, with hydrogen nuclei being fused into helium nuclei. Through these reactions, more than 4 million tons of matter are converted into energy each second, producing neutrinos and solar radiation. Current theory predicts that in about five billion years, the Sun will evolve into a red giant and then a white dwarf, creating a planetary nebula in the process.

The Sun is a magnetically active star. It supports a strong, changing magnetic field that varies year-to-year and reverses direction about every 11 years. The Sun's magnetic field gives rise to many effects that are collectively called solar activity. They include sunspots on the Sun's surface, solar flares, and variations in the solar wind that carry material through the solar system. The effects of solar activity on Earth include auroras at moderate to high latitudes, and the disruption of radio communications and electric power. Solar activity is thought to have played a large role in the formation and evolution of the solar system, and strongly affects the structure of the Earth's outer atmosphere.

Although it is the nearest star to Earth and has been intensively studied by scientists, many questions about the Sun remain unanswered. For instance, we do not know why its outer atmosphere has a temperature of over a million K while its visible surface (the photosphere) has a temperature of just 6,000 K. Current topics of scientific inquiry include the Sun's regular cycle of sunspot activity, the physics and origin of solar flares and prominences, the magnetic interaction between the chromosphere and the corona, and the origin of the solar wind.

The Sun is sometimes referred to by its Latin name Sol or its Greek name Helios. Its astrological and astronomical symbol is a circle with a point at its center: Some ancient peoples of the world considered it a planet.

General information

The Sun as it appears through a camera lens from the Earth's surface.

The Sun is placed in a spectral class called G2V. "G2" means that it has a surface temperature of approximately 5,500 K, giving it a white color. As a consequence of light scattering by the Earth's atmosphere, it appears yellow to us. Its spectrum contains lines of ionized and neutral metals, as well as very weak hydrogen lines. The "V" suffix indicates that the Sun, like most stars, is a main sequence star. This means that it generates its energy by nuclear fusion of hydrogen nuclei into helium and is in a state of hydrostatic balance—neither contracting nor expanding over time. There are more than 100 million G2 class stars in our galaxy. Due to logarithmic size distribution, the Sun is actually brighter than 85 percent of the stars in the Galaxy, most of which are red dwarfs.

The Sun will spend a total of approximately 10 billion years as a main sequence star. Its current age, determined using computer models of stellar evolution and nucleocosmochronology, is thought to be about 4.57 billion years. The Sun orbits the center of the Milky Way galaxy at a distance of about 25,000 to 28,000 light-years from the galactic center, completing one revolution in about 225–250 million years. The orbital speed is 220 km/s, equivalent to one light-year every 1,400 years, and one AU every 8 days.

It is suggested that the Sun is a third generation star, whose formation may have been triggered by shockwaves from a nearby supernova based on a high abundance of heavy elements such as gold and uranium in the solar system. These elements could most plausibly have been produced by endergonic nuclear reactions during a supernova, or by transmutation via neutron absorption inside a massive second-generation star.

The Sun does not have enough mass to explode as a supernova. Instead, in 4–5 billion years, it will enter a red giant phase, its outer layers expanding as the hydrogen fuel in the core is consumed and the core contracts and heats up. Helium fusion will begin when the core temperature reaches about 3×10⁸ K. While it is likely that the expansion of the outer layers of the Sun will reach the current position of Earth's orbit, recent research suggests that mass lost from the Sun earlier in its red giant phase will cause the Earth's orbit to move further out, preventing it from being engulfed. However, Earth's water and most of the atmosphere will be boiled away.

Following the red giant phase, intense thermal pulsations will cause the Sun to throw off its outer layers, forming a planetary nebula. The Sun will then evolve into a white dwarf, slowly cooling over eons. This stellar evolution scenario is typical of low- to medium-mass stars.

Sunlight is the main source of energy near the surface of Earth. The solar constant is the amount of power that the Sun deposits per unit area that is directly exposed to sunlight. The solar constant is equal to approximately 1,370 watts per square meter of area at a distance of one AU from the Sun (that is, on or near Earth). Sunlight on the surface of Earth is attenuated by the Earth's atmosphere so that less power arrives at the surface—closer to 1,000 watts per directly exposed square meter in clear conditions when the Sun is near the zenith. This energy can be harnessed via a variety of natural and synthetic processes—photosynthesis by plants captures the energy of sunlight and converts it to chemical form (oxygen and reduced carbon compounds), while direct heating or electrical conversion by solar cells are used by solar power equipment to generate electricity or to do other useful work. The energy stored in petroleum and other fossil fuels was originally converted from sunlight by photosynthesis in the distant past.

Sunlight has several interesting biological properties. Ultraviolet light from the Sun has antiseptic properties and can be used to sterilize tools. It also causes sunburn, and has other medical effects such as the production of Vitamin D. Ultraviolet light is strongly attenuated by Earth's atmosphere, so that the amount of UV varies greatly with latitude due the longer passage of sunlight through the atmosphere at high latitudes. This variation is responsible for many biological adaptations, including variations in human skin color in different regions of the globe.

Observed from Earth, the path of the Sun across the sky varies throughout the year. The shape described by the Sun's position, considered at the same time each day for a complete year, is called the analemma and resembles a figure 8 aligned along a North/South axis. While the most obvious variation in the Sun's apparent position through the year is a North/South swing over 47 degrees of angle (due to the 23.5-degree tilt of the Earth with respect to the Sun), there is an East/West component as well. The North/South swing in apparent angle is the main source of seasons on Earth.

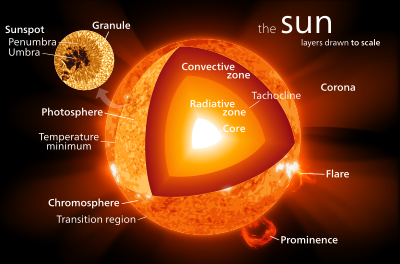
Structure

The sun is an averaged-sized star. It contains about 99 percent of the total mass of the solar system. The volume of the Sun is 1,303,600 times that of the Earth; 71 percent of hydrogen makes up the mass of the Sun.

Did you know?

The Sun is a near-perfect sphere

The Sun is a near-perfect sphere, with an oblateness estimated at about 9 millionths, which means that its polar diameter differs from its equatorial diameter by only 10 km. While the Sun does not rotate as a solid body (the rotational period is 25 days at the equator and about 35 days at the poles), it takes approximately 28 days to complete one full rotation; the centrifugal effect of this slow rotation is 18 million times weaker than the surface gravity at the Sun's equator. Tidal effects from the planets do not significantly affect the shape of the Sun, although the Sun itself orbits the center of mass of the solar system, which is located nearly a solar radius away from the center of the Sun mostly because of the large mass of Jupiter.

The Sun does not have a definite boundary as rocky planets do; the density of its gases drops approximately exponentially with increasing distance from the center of the Sun. Nevertheless, the Sun has a well-defined interior structure, described below. The Sun's radius is measured from its center to the edge of the photosphere. This is simply the layer below which the gases are thick enough to be opaque but above which they are transparent; the photosphere is the surface most readily visible to the naked eye. Most of the Sun's mass lies within about 0.7 radii of the center.

The solar interior is not directly observable, and the Sun itself is opaque to electromagnetic radiation. However, just as seismology uses waves generated by earthquakes to reveal the interior structure of the Earth, the discipline of helioseismology makes use of pressure waves traversing the Sun's interior to measure and visualize the Sun's inner structure. Computer modeling of the Sun is also used as a theoretical tool to investigate its deeper layers.

Core

Structure of the Sun

The temperature of sun's surface is about 5,800 K. The temperature at its core has been estimated about 15,000,000 K. Energy is produced in its core by nuclear fusion, converts hydrogen atoms and releases huge amounts of energy. it is the same reaction that occurs in a hydrogen bomb. The American physicist George Gamow had once calculated that if a pinhead could be brought to the same temperature, as at the core of the sun, it would set fire to everything for 100 kilometres around. At the center of the Sun, where its density reaches up to 150,000 kg/m³ (150 times the density of water on Earth), thermonuclear reactions (nuclear fusion) convert hydrogen into helium, releasing the energy that keeps the Sun in a state of equilibrium. About 8.9×10³⁷ protons (hydrogen nuclei) are converted into helium nuclei every second, releasing energy at the matter-energy conversion rate of 4.26 million metric tons per second, 383 yottawatts (383×10²⁴ W) or 9.15×10¹⁰ megatons of TNT per second. The fusion rate in the core is in a self-correcting equilibrium: a slightly higher rate of fusion would cause the core to heat up more and expand slightly against the weight of the outer layers, reducing the fusion rate and correcting the perturbation; and a slightly lower rate would cause the core to shrink slightly, increasing the fusion rate and again reverting it to its present level.

The core extends from the center of the Sun to about 0.2 solar radii, and is the only part of the Sun in which an appreciable amount of heat is produced by fusion; the rest of the star is heated by energy that is transferred outward. All of the energy produced by interior fusion must travel through many successive layers to the solar photosphere before it escapes into space.

The high-energy photons (gamma and X-rays) released in fusion reactions take a long time to reach the Sun's surface, slowed down by the indirect path taken, as well as by constant absorption and reemission at lower energies in the solar mantle. Estimates of the "photon travel time" range from between 10,000 and 170,000 years. After a final trip through the convective outer layer to the transparent "surface" of the photosphere, the photons escape as visible light. Each gamma ray in the Sun's core is converted into several million visible light photons before escaping into space. Neutrinos are also released by the fusion reactions in the core, but unlike photons they very rarely interact with matter, so almost all are able to escape the Sun immediately. For many years measurements of the number of neutrinos produced in the Sun were much lower than theories predicted, a problem which was recently resolved through a better understanding of the effects of neutrino oscillation.

Radiation zone

From about 0.2 to about 0.7 solar radii, solar material is hot and dense enough that thermal radiation is sufficient to transfer the intense heat of the core outward. In this zone there is no thermal convection; while the material grows cooler as altitude increases, this temperature gradient is too low to drive convection. Heat is transferred by radiation—ions of hydrogen and helium emit photons, which travel a brief distance before being reabsorbed by other ions.

Convection zone

From about 0.7 solar radii to the Sun's visible surface, the material in the Sun is not dense enough or hot enough to transfer the heat energy of the interior outward via radiation. As a result, thermal convection occurs as thermal columns carry hot material to the surface (photosphere) of the Sun. Once the material cools off at the surface, it plunges back downward to the base of the convection zone, to receive more heat from the top of the radiative zone. Convective overshoot is thought to occur at the base of the convection zone, carrying turbulent downflows into the outer layers of the radiative zone.

The thermal columns in the convection zone form an imprint on the surface of the Sun, in the form of the solar granulation and supergranulation. The turbulent convection of this outer part of the solar interior gives rise to a "small-scale" dynamo that produces magnetic north and south poles all over the surface of the Sun.

Photosphere

The visible surface of the Sun, the photosphere, is the layer below which the Sun becomes opaque to visible light. Above the photosphere visible sunlight is free to propagate into space, and its energy escapes the Sun entirely. The change in opacity is due to the decreasing amount of H⁻ ions, which absorb visible light easily. Conversely, the visible light we see is produced as electrons react with hydrogen atoms to produce H⁻ ions. Sunlight has approximately a black-body spectrum that indicates its temperature is about 6,000 K(10,340 °F / 5,727 °C), interspersed with atomic absorption lines from the tenuous layers above the photosphere. The photosphere has a particle density of about 10²³/m³ (this is about 1 percent of the particle density of Earth's atmosphere at sea level).

During early studies of the optical spectrum of the photosphere, some absorption lines were found that did not correspond to any chemical elements then known on Earth. In 1868, Norman Lockyer hypothesized that these absorption lines were due to a new element which he dubbed "helium," after the Greek Sun god Helios. It was not until 25 years later that helium was isolated on Earth.

Atmosphere

During a total solar eclipse, the sun's atmosphere is more apparent to the eye.

The parts of the Sun above the photosphere are referred to collectively as the solar atmosphere. They can be viewed with telescopes operating across the electromagnetic spectrum, from radio through visible light to gamma rays, and comprise five principal zones: the temperature minimum, the chromosphere, the transition region, the corona, and the heliosphere. The heliosphere, which may be considered the tenuous outer atmosphere of the Sun, extends outward past the orbit of Pluto to the heliopause, where it forms a sharp shock front boundary with the interstellar medium. The chromosphere, transition region, and corona are much hotter than the surface of the Sun; the reason why is not yet known.

The coolest layer of the Sun is a temperature minimum region about 500 km above the photosphere, with a temperature of about 4,000 K. This part of the Sun is cool enough to support simple molecules such as carbon monoxide and water, which can be detected by their absorption spectra. Above the temperature minimum layer is a thin layer about 2,000 km thick, dominated by a spectrum of emission and absorption lines. It is called the chromosphere from the Greek root chroma, meaning color, because the chromosphere is visible as a colored flash at the beginning and end of total eclipses of the Sun. The temperature in the chromosphere increases gradually with altitude, ranging up to around 100,000 K near the top.

Above the chromosphere is a transition region in which the temperature rises rapidly from around 100,000 K to coronal temperatures closer to one million K. The increase is due to a phase transition as helium within the region becomes fully ionized by the high temperatures. The transition region does not occur at a well-defined altitude. Rather, it forms a kind of nimbus around chromospheric features such as spicules and filaments, and is in constant, chaotic motion. The transition region is not easily visible from Earth's surface, but is readily observable from space by instruments sensitive to the far ultraviolet portion of the spectrum.

The corona is the extended outer atmosphere of the Sun, which is much larger in volume than the Sun itself. The corona merges smoothly with the solar wind that fills the solar system and heliosphere. The low corona, which is very near the surface of the Sun, has a particle density of 10¹⁴/m³-10¹⁶/m³. (Earth's atmosphere near sea level has a particle density of about 2x10²⁵/m³.) The temperature of the corona is several million kelvin. While no complete theory yet exists to account for the temperature of the corona, at least some of its heat is known to be due to magnetic reconnection.

The heliosphere extends from approximately 20 solar radii (0.1 AU) to the outer fringes of the solar system. Its inner boundary is defined as the layer in which the flow of the solar wind becomes superalfvénic - that is, where the flow becomes faster than the speed of Alfvén waves. Turbulence and dynamic forces outside this boundary cannot affect the shape of the solar corona within, because the information can only travel at the speed of Alfvén waves. The solar wind travels outward continuously through the heliosphere, forming the solar magnetic field into a spiral shape, until it impacts the heliopause more than 50 AU from the Sun. In December 2004, the Voyager 1 probe passed through a shock front that is thought to be part of the heliopause. Both of the Voyager probes have recorded higher levels of energetic particles as they approach the boundary.

Solar Activity

Sunspots and the solar cycle

Measurements of solar cycle variation during the last 30 years

When observing the Sun with appropriate filtration, the most immediately visible features are usually its sunspots, which are well-defined surface areas that appear darker than their surroundings due to lower temperatures. Sunspots are regions of intense magnetic activity where energy transport is inhibited by strong magnetic fields. They are often the source of intense flares and coronal mass ejections. The largest sunspots can be tens of thousands of kilometers across.

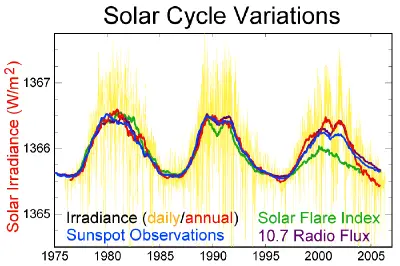
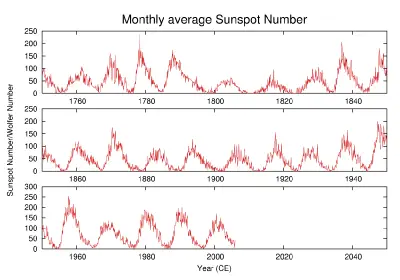
The number of sunspots visible on the Sun is not constant, but varies over a 10-12 year cycle known as the Solar cycle. At a typical solar minimum, few sunspots are visible, and occasionally none at all can be seen. Those that do appear are at high solar latitudes. As the sunspot cycle progresses, the number of sunspots increases and they move closer to the equator of the Sun, a phenomenon described by Spörer's law. Sunspots usually exist as pairs with opposite magnetic polarity. The polarity of the leading sunspot alternates every solar cycle, so that it will be a north magnetic pole in one solar cycle and a south magnetic pole in the next.

History of the number of observed sunspots during the last 250 years, which shows the ~11 year solar cycle.

The solar cycle has a great influence on space weather, and seems also to have a strong influence on the Earth's climate. Solar minima tend to be correlated with colder temperatures, and longer than average solar cycles tend to be correlated with hotter temperatures. In the 17th century, the solar cycle appears to have stopped entirely for several decades; very few sunspots were observed during the period. During this era, which is known as the Maunder minimum or Little Ice Age, Europe experienced very cold temperatures. Earlier extended minima have been discovered through analysis of tree rings and also appear to have coincided with lower-than-average global temperatures.

Effects on Earth and other bodies

Solar activity has several effects on the Earth and its surroundings. Because the Earth has a magnetic field, charged particles from the solar wind cannot impact the atmosphere directly, but are instead deflected by the magnetic field and aggregate to form the Van Allen belts. The Van Allen belts consist of an inner belt composed primarily of protons and an outer belt composed mostly of electrons. Radiation within the Van Allen belts can occasionally damage satellites passing through them.

The Van Allen belts form arcs around the Earth with their tips near the north and south poles. The most energetic particles can 'leak out' of the belts and strike the Earth's upper atmosphere, causing auroras, known as aurorae borealis in the northern hemisphere and aurorae australis in the southern hemisphere. In periods of normal solar activity, aurorae can be seen in oval-shaped regions centered on the magnetic poles and lying roughly at a geomagnetic latitude of 65°, but at times of high solar activity the auroral oval can expand greatly, moving towards the equator. Aurorae borealis have been observed from locales as far south as Mexico.

Solar wind also affects the surfaces of Mercury, Moon, and asteroids in the form of space weathering Because they do not have any substantial atmosphere, solar wind ions hit their surface materials and either alter the atomic structure of the materials or form a thin coating containing submicroscopic (or nanophase) metallic iron particles. The space weathering effect has been puzzling researchers working on planetary remote geochemical analysis until recently.

Theoretical problems

Solar neutrino problem

For many years the number of solar electron neutrinos detected on Earth was only a third of the number expected, according to theories describing the nuclear reactions in the Sun. This anomalous result was termed the solar neutrino problem. Theories proposed to resolve the problem either tried to reduce the temperature of the Sun's interior to explain the lower neutrino flux, or posited that electron neutrinos could oscillate, that is, change into undetectable tau and muon neutrinos as they traveled between the Sun and the Earth. Several neutrino observatories were built in the 1980s to measure the solar neutrino flux as accurately as possible, including the Sudbury Neutrino Observatory and Kamiokande. Results from these observatories eventually led to the discovery that neutrinos have a very small rest mass and can indeed oscillate.. Moreover, the Sudbury Neutrino Observatory was able to detect all three types of neutrinos directly, and found that the Sun's total neutrino emission rate agreed with the Standard Solar Model, although only one-third of the neutrinos seen at Earth were of the electron type.

Coronal heating problem

The optical surface of the Sun (the photosphere) is known to have a temperature of approximately 6,000 K. Above it lies the solar corona at a temperature of 1,000,000 K. The high temperature of the corona shows that it is heated by something other than the photosphere.

It is thought that the energy necessary to heat the corona is provided by turbulent motion in the convection zone below the photosphere, and two main mechanisms have been proposed to explain coronal heating. The first is wave heating, in which sound, gravitational and magnetohydrodynamic waves are produced by turbulence in the convection zone. These waves travel upward and dissipate in the corona, depositing their energy in the ambient gas in the form of heat. The other is magnetic heating, in which magnetic energy is continuously built up by photospheric motion and released through magnetic reconnection in the form of large solar flares and myriad similar but smaller events.

Currently, it is unclear whether waves are an efficient heating mechanism. All waves except Alfven waves have been found to dissipate or refract before reaching the corona. In addition, Alfven waves do not easily dissipate in the corona. Current research focus has therefore shifted towards flare heating mechanisms. One possible candidate to explain coronal heating is continuous flaring at small scales, but this remains an open topic of investigation.

Faint young sun problem

Theoretical models of the sun's development suggest that 3.8 to 2.5 billion years ago, during the Archean period, the Sun was only about 75% as bright as it is today. Such a weak star would not have been able to sustain liquid water on the Earth's surface, and thus life should not have been able to develop. However, the geological record demonstrates that the Earth has remained at a fairly constant temperature throughout its history, and in fact that the young Earth was somewhat warmer than it is today. The general consensus among scientists is that the young Earth's atmosphere contained much larger quantities of greenhouse gases (such as carbon dioxide and/or ammonia) than are present today, which trapped enough heat to compensate for the lesser amount of solar energy reaching the planet.

Magnetic Field

The heliospheric current sheet extends to the outer reaches of the Solar System, and results from the influence of the Sun's rotating magnetic field on the plasma in the interplanetary medium

All matter in the Sun is in the form of gas and plasma due to its high temperatures. This makes it possible for the Sun to rotate faster at its equator (about 25 days) than it does at higher latitudes (about 35 days near its poles). The differential rotation of the Sun's latitudes causes its magnetic field lines to become twisted together over time, causing magnetic field loops to erupt from the Sun's surface and trigger the formation of the Sun's dramatic sunspots and solar prominences (see magnetic reconnection). This twisting action gives rise to the solar dynamo and an 11-year solar cycle of magnetic activity as the Sun's magnetic field reverses itself about every 11 years.

The influence of the Sun's rotating magnetic field on the plasma in the interplanetary medium creates the heliospheric current sheet, which separates regions with magnetic fields pointing in different directions. The plasma in the interplanetary medium is also responsible for the strength of the Sun's magnetic field at the orbit of the Earth. If space were a vacuum, then the Sun's 10^-4 tesla magnetic dipole field would reduce with the cube of the distance to about 10^-11 tesla. But satellite observations show that it is about 100 times greater at around 10^-9 tesla. Magnetohydrodynamic (MHD) theory predicts that the motion of a conducting fluid (e.g., the interplanetary medium) in a magnetic field, induces electric currents which in turn generates magnetic fields, and in this respect it behaves like an MHD dynamo.

History of solar observation

Early understanding of the Sun

The Trundholm sun chariot pulled by a horse is a sculpture believed to be illustrating an important part of Nordic Bronze Age mythology.

Humanity's most fundamental understanding of the Sun is as the luminous disk in the heavens, whose presence above the horizon creates day and whose absence causes night. In many prehistoric and ancient cultures, the Sun was thought to be a solar deity or other supernatural phenomenon, and worship of the Sun was central to civilizations such as the Inca of South America and the Aztecs of what is now Mexico. Many ancient monuments were constructed with solar phenomena in mind; for example, stone megaliths accurately mark the summer solstice (some of the most prominent megaliths are located in Nabta Playa, Egypt, and at Stonehenge in England); the pyramid of El Castillo at Chichén Itzá in Mexico is designed to cast shadows in the shape of serpents climbing the pyramid at the vernal and autumn equinoxes. With respect to the fixed stars, the Sun appears from Earth to revolve once a year along the ecliptic through the zodiac, and so the Sun was considered by Greek astronomers to be one of the seven planets (Greek planetes, "wanderer"), after which the seven days of the week are named in some languages.

Development of modern scientific understanding

One of the first people in the Western world to offer a scientific explanation for the sun was the Greek philosopher Anaxagoras, who reasoned that it was a giant flaming ball of metal even larger than the Peloponnesus, and not the chariot of Helios. For teaching this heresy, he was imprisoned by the authorities and sentenced to death (though later released through the intervention of Pericles).

Another scientist to challenge the accepted view was Nicolaus Copernicus, who in the sixteenth century developed the theory that the Earth orbited the Sun, rather than the other way around. In the early seventeenth century, Galileo pioneered telescopic observations of the Sun, making some of the first known observations of sunspots and positing that they were on the surface of the Sun rather than small objects passing between the Earth and the Sun. Sir Isaac Newton observed the Sun's light using a prism, and showed that it was made up of light of many colors, while in 1800 William Herschel discovered infrared radiation beyond the red part of the solar spectrum. The 1800s saw spectroscopic studies of the Sun advance, and Joseph von Fraunhofer made the first observations of absorption lines in the spectrum, the strongest of which are still often referred to as Fraunhofer lines.

In the early years of the modern scientific era, the source of the Sun's energy was a significant puzzle. Among the proposals were that the Sun extracted its energy from friction of its gas masses, or that its energy was derived from gravitational potential energy released as it continuously contracted. Either of these sources of energy could only power the Sun for a few million years at most, but geologists were showing that the Earth's age was several billion years. Nuclear fusion was first proposed as the source of solar energy only in the 1930s, when Hans Bethe calculated the details of the two main energy-producing nuclear reactions that power the Sun.

Solar space missions

A solar prominence erupts in August 2012, as captured by SDO

The first satellites designed to observe the Sun were NASA's Pioneers 5, 6, 7, 8 and 9, which were launched between 1959 and 1968. These probes orbited the Sun at a distance similar to that of the Earth's orbit, and made the first detailed measurements of the solar wind and the solar magnetic field. Pioneer 9 operated for a particularly long period of time, transmitting data until 1983.

In the 1970s, Helios 1 and the Skylab Apollo Telescope Mount provided scientists with significant new data on solar wind and the solar corona. The Helios 1 satellite was a joint U.S.-German probe that studied the solar wind from an orbit carrying the spacecraft inside Mercury's orbit at perihelion. The Skylab space station, launched by NASA in 1973, included a solar observatory module called the Apollo Telescope Mount that was operated by astronauts resident on the station. Skylab made the first time-resolved observations of the solar transition region and of ultraviolet emissions from the solar corona. Discoveries included the first observations of coronal mass ejections, then called "coronal transients," and of coronal holes, now known to be intimately associated with the solar wind.

In 1980, the Solar Maximum Mission was launched by NASA. This spacecraft was designed to observe gamma rays, X-rays and UV radiation from solar flares during a time of high solar activity. Just a few months after launch, however, an electronics failure caused the probe to go into standby mode, and it spent the next three years in this inactive state. In 1984 Space Shuttle Challenger mission STS-41C retrieved the satellite and repaired its electronics before re-releasing it into orbit. The Solar Maximum Mission subsequently acquired thousands of images of the solar corona before re-entering the Earth's atmosphere in June 1989.

Japan's Yohkoh (Sunbeam) satellite, launched in 1991, observed solar flares at X-ray wavelengths. Mission data allowed scientists to identify several different types of flares, and also demonstrated that the corona away from regions of peak activity was much more dynamic and active than had previously been supposed. Yohkoh observed an entire solar cycle but went into standby mode when an annular eclipse in 2001 caused it to lose its lock on the Sun. It was destroyed by atmospheric reentry in 2005.

One of the most important solar missions to date has been the Solar and Heliospheric Observatory, jointly built by the European Space Agency and NASA and launched on December 2, 1995. Originally a two-year mission, SOHO has operated for more than a decade. It proved so useful that a follow-on mission, the Solar Dynamics Observatory (SDO), was launched in February 2010. Situated at the Lagrangian point between the Earth and the Sun (at which the gravitational pull from both is equal), SOHO has provided a constant view of the Sun at many wavelengths since its launch. In addition to its direct solar observation, SOHO has enabled the discovery of large numbers of comets, mostly very tiny sungrazing comets which incinerate as they pass the Sun.

All these satellites have observed the Sun from the plane of the ecliptic, and so have only observed its equatorial regions in detail. The Ulysses probe was launched in 1990 to study the Sun's polar regions. It first traveled to Jupiter, to 'slingshot' past the planet into an orbit which would take it far above the plane of the ecliptic. Serendipitously, it was well-placed to observe the collision of Comet Shoemaker-Levy 9 with Jupiter in 1994. Once Ulysses was in its scheduled orbit, it began observing the solar wind and magnetic field strength at high solar latitudes, finding that the solar wind from high latitudes was moving at about 750 km/s (slower than expected), and that there were large magnetic waves emerging from high latitudes which scattered galactic cosmic rays.

Elemental abundances in the photosphere are well known from spectroscopic studies, but the composition of the interior of the Sun is more poorly understood. A solar wind sample return mission, Genesis, was designed to allow astronomers to directly measure the composition of solar material. Genesis returned to Earth in 2004 but was damaged by a crash landing after its parachute failed to deploy on reentry into Earth's atmosphere. Despite severe damage, some usable samples have been recovered from the spacecraft's sample return module and are undergoing analysis.

Sun observation and eye damage

Sunlight is very bright, and looking directly at the Sun with the naked eye for brief periods can be painful, but is generally not hazardous. Looking directly at the Sun causes phosphene visual artifacts and temporary partial blindness. It also delivers about 4 milliwatts of sunlight to the retina, slightly heating it and potentially (though not normally) damaging it. UV exposure gradually yellows the lens of the eye over a period of years and can cause cataracts, but those depend on general exposure to solar UV, not on whether one looks directly at the Sun.

Viewing the Sun through light-concentrating optics such as binoculars is very hazardous without an attenuating (ND) filter to dim the sunlight. Using a proper filter is important as some improvised filters pass UV rays that can damage the eye at high brightness levels. Unfiltered binoculars can deliver over 500 times more sunlight to the retina than does the naked eye, killing retinal cells almost instantly. Even brief glances at the midday Sun through unfiltered binoculars can cause permanent blindness. One way to view the Sun safely is by projecting an image onto a screen using binoculars or a small telescope.

Partial solar eclipses are hazardous to view because the eye's pupil is not adapted to the unusually high visual contrast: the pupil dilates according to the total amount of light in the field of view, not by the brightest object in the field. During partial eclipses most sunlight is blocked by the Moon passing in front of the Sun, but the uncovered parts of the photosphere have the same surface brightness as during a normal day. In the overall gloom, the pupil expands from ~2 mm to ~6 mm, and each retinal cell exposed to the solar image receives about ten times more light than it would looking at the non-eclipsed sun. This can damage or kill those cells, resulting in small permanent blind spots for the viewer. The hazard is insidious for inexperienced observers and for children, because there is no perception of pain: it is not immediately obvious that one's vision is being destroyed.

During sunrise and sunset, sunlight is attenuated through rayleigh and mie scattering of light by a particularly long passage through Earth's atmosphere, and the direct Sun is sometimes faint enough to be viewed directly without discomfort or safely with binoculars. Hazy conditions, atmospheric dust, and high humidity contribute to this atmospheric attenuation.

References

ISBN links support NWE through referral fees

• Alfven, H. "Magneto-hydrodynamic waves, and the heating of the solar corona." Monthly Notices of the Royal Astronomical Society 107 (1947): 211.
• Bethe, H. "On the Formation of Deuterons by Proton Combination." Physical Review 54 (1938): 862-862.
• Bethe, H. "Energy Production in Stars." Physical Review 55 (1939): 434-456.
• Hapke, B. "Space weathering from Mercury to the asteroid belt." J. Geophys. Res. 106(10) (2001): 039-10, 073.
• Kasting, J.F., and T.P. Ackerman. "Climatic Consequences of Very High Carbon Dioxide Levels in the Earth’s Early Atmosphere." Science 234 (1986): 1383-1385.
• Lean, J., A. Skumanich, and O. White. "Estimating the Sun's radiative output during the Maunder Minimum." Geophysical Research Letters 19 (1992): 1591-1594.
• Lewis, R. The Illustrated Encyclopedia of the Universe. New York: Harmony Books, 1983.
• Schlattl, H. "Three-flavor oscillation solutions for the solar neutrino problem." Physical Review D 64(1) (2001).

External links

All links retrieved February 26, 2023.

• NASA Eclipse homepage
• (Solar & Heliospheric Observatory) satellite
• Latest SOHO images
• Solar Sounds
• Spaceweather.com
• Sun Science World
• A collection of solar movies
• NASA/Marshall Solar Physics website
• Eclipse Links

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Sun  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Sun"

Note: Some restrictions may apply to use of individual images which are separately licensed.