Nuclear fusion
In physics and nuclear chemistry, nuclear fusion is the process by which multiple atomic particles join together to form a heavier nucleus. It is accompanied by the release or absorption of energy. Iron and nickel nuclei have the largest binding energies per nucleon of all nuclei and therefore are the most stable. The fusion of two nuclei lighter than iron or nickel generally releases energy, while the fusion of nuclei heavier than iron or nickel absorbs energy. The opposite is true for nuclear fission. Nuclear fusion is naturally found in stars.
Overview
| Nuclear physics | ||||||||||||||
| ||||||||||||||
| Radioactive decay Nuclear fission Nuclear fusion
| ||||||||||||||
Fusion reactions power the stars and produce all but the lightest elements in a process called nucleosynthesis. Whereas the fusion of light elements in the stars releases energy, production of the heaviest elements absorbs energy, so it can only take place in the extremely high-energy conditions of supernova explosions.
When the fusion reaction is a sustained uncontrolled chain, it can result in a thermonuclear explosion, such as what is generated by a hydrogen bomb. Reactions that are not self-sustaining can still release considerable energy, as well as large numbers of neutrons.
Research into controlled fusion, with the aim of producing fusion power for the production of electricity, has been conducted for over 50 years. It has been accompanied by extreme scientific and technological difficulties, and as of yet has not been successful in producing workable designs. As of the present, the only self-sustaining fusion reactions produced by humans have been produced in hydrogen bombs, where the extreme power of a fission bomb is necessary to begin the process. While some plans have been put forth to attempt to use the explosions of hydrogen bombs to generate electricity (e.g. PACER), none of these have ever moved far past the design stage.
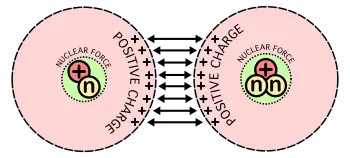
It takes considerable energy to force nuclei to fuse, even those of the lightest element, hydrogen. This is because all nuclei have a positive charge (due to their protons), and as like charges repel, nuclei strongly resist being put too close together. Accelerated to high speeds (that is, heated to thermonuclear temperatures), however, they can overcome this electromagnetic repulsion and get close enough for the strong nuclear force to be active, achieving fusion. The fusion of lighter nuclei, creating a heavier nucleus and a free neutron, will generally release more energy than it took to force them together‚ÄĒan exothermic process that can produce self-sustaining reactions.
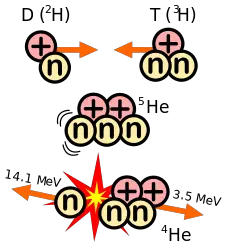
The energy released in most nuclear reactions is much larger than that in chemical reactions, because the binding energy that holds a nucleus together is far greater than the energy that holds electrons to a nucleus. For example, the ionization energy gained by adding an electron to a hydrogen nucleus is 13.6 electron volts‚ÄĒless than one-millionth of the 17¬†MeV released in the D-T (deuterium-tritium) reaction shown to the top right. Fusion reactions have an energy density many times greater than nuclear fission‚ÄĒthat is, per unit of mass the reactions produce far greater energies, even though individual fission reactions are generally much more energetic than individual fusion reactions‚ÄĒwhich are themselves millions of times more energetic than chemical reactions. Only the direct conversion of mass into energy, such as with collision of matter and antimatter, is more energetic per unit of mass than nuclear fusion.
Building upon the nuclear transmutation experiments of Ernest Rutherford done a few years earlier, fusion of light nuclei (hydrogen isotopes) was first observed by Mark Oliphant in 1932, and the steps of the main cycle of nuclear fusion in stars were subsequently worked out by Hans Bethe throughout the remainder of that decade. Research into fusion for military purposes began in the early 1940s, as part of the Manhattan Project, but was not successful until 1952. Research into controlled fusion for civilian purposes began in the 1950s, and continues to this day.
Requirements
A substantial energy barrier must be overcome before fusion can occur. At large distances two naked nuclei repel one another because of the repulsive electrostatic force between their positively charged protons. If two nuclei can be brought close enough together, however, the electrostatic repulsion can be overcome by the nuclear force which is stronger at close distances.
When a nucleon such as a proton or neutron is added to a nucleus, the nuclear force attracts it to other nucleons, but primarily to its immediate neighbors due to the short range of the force. The nucleons in the interior of a nucleus have more neighboring nucleons than those on the surface. Since smaller nuclei have a larger surface area-to-volume ratio, the binding energy per nucleon due to the strong force generally increases with the size of the nucleus but approaches a limiting value corresponding to that of a fully surrounded nucleon.
The electrostatic force, on the other hand, is an inverse-square force, so a proton added to a nucleus will feel an electrostatic repulsion from all the other protons in the nucleus. The electrostatic energy per nucleon due to the electrostatic force thus increases without limit as nuclei get larger.
The net result of these opposing forces is that the binding energy per nucleon generally increases with increasing size, up to the elements iron and nickel, and then decreases for heavier nuclei. Eventually, the binding energy becomes negative and very heavy nuclei are not stable. The four most tightly bound nuclei, in decreasing order of binding energy, are 62Ni, 58Fe, 56Fe, and 60Ni.[1] Even though the nickel isotope]] 62Ni is more stable, the iron isotope 56Fe is an order of magnitude more common. This is due to a greater disintegration rate for 62Ni in the interior of stars driven by photon absorption.
A notable exception to this general trend is the helium-4 nucleus, whose binding energy is higher than that of lithium, the next heavier element. The Pauli exclusion principle provides an explanation for this exceptional behavior‚ÄĒit says that because protons and neutrons are fermions, they cannot exist in exactly the same state. Each proton or neutron energy state in a nucleus can accommodate both a spin up particle and a spin down particle. Helium-4 has an anomalously large binding energy because its nucleus consists of two protons and two neutrons; so all four of its nucleons can be in the ground state. Any additional nucleons would have to go into higher energy states.
The situation is similar if two nuclei are brought together. As they approach each other, all the protons in one nucleus repel all the protons in the other. Not until the two nuclei actually come in contact can the strong nuclear force take over. Consequently, even when the final energy state is lower, there is a large energy barrier that must first be overcome. It is called the Coulomb barrier.
The Coulomb barrier is smallest for isotopes of hydrogen‚ÄĒthey contain only a single positive charge in the nucleus. A bi-proton is not stable, so neutrons must also be involved, ideally in such a way that a helium nucleus, with its extremely tight binding, is one of the products.
Using deuterium-tritium fuel, the resulting energy barrier is about 0.01 MeV. In comparison, the energy needed to remove an electron from hydrogen is 13.6 eV, about 750 times less energy. The (intermediate) result of the fusion is an unstable 5He nucleus, which immediately ejects a neutron with 14.1 MeV. The recoil energy of the remaining 4He nucleus is 3.5 MeV, so the total energy liberated is 17.6 MeV. This is many times more than what was needed to overcome the energy barrier.
If the energy to initiate the reaction comes from accelerating one of the nuclei, the process is called beam-target fusion; if both nuclei are accelerated, it is beam-beam fusion. If the nuclei are part of a plasma near thermal equilibrium, one speaks of thermonuclear fusion. Temperature is a measure of the average kinetic energy of particles, so by heating the nuclei they will gain energy and eventually have enough to overcome this 0.01¬†MeV. Converting the units between electron-volts and Kelvin shows that the barrier would be overcome at a temperature in excess of 120 million Kelvin‚ÄĒa very high temperature.
There are two effects that lower the actual temperature needed. One is the fact that temperature is the average kinetic energy, implying that some nuclei at this temperature would actually have much higher energy than 0.01 MeV, while others would be much lower. It is the nuclei in the high-energy tail of the velocity distribution that account for most of the fusion reactions. The other effect is quantum tunneling. The nuclei do not actually have to have enough energy to overcome the Coulomb barrier completely. If they have nearly enough energy, they can tunnel through the remaining barrier. For this reason fuel at lower temperatures will still undergo fusion events at a lower rate.
The reaction cross section ŌÉ is a measure of the probability of a fusion reaction as a function of the relative velocity of the two reactant nuclei. If the reactants have a distribution of velocities, e.g. a thermal distribution with thermonuclear fusion, then it is useful to perform an average over the distributions of the product of cross section and velocity. The reaction rate (fusions per volume per time) is <ŌÉv> times the product of the reactant number densities:
If a species of nuclei is reacting with itself, such as the DD reaction, then the product must be replaced by .
increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of 10‚Äď100¬†keV. At these temperatures, well above typical ionization energies (13.6¬†eV in the hydrogen case), the fusion reactants exist in a plasma state.
The significance of <ŌÉv> as a function of temperature in a device with a particular energy confinement time is found by considering the Lawson criterion.
Fuel confinement methods
Gravitational
One force capable of confining the fuel well enough to satisfy the Lawson criterion is gravity. The mass needed, however, is so great that gravitational confinement is only found in stars (the smallest of which are brown dwarfs). Even if the more reactive fuel deuterium were used, a mass greater than that of the planet Jupiter would be needed.
Magnetic
Since plasmas are very good electrical conductors, magnetic fields can also confine fusion fuel. A variety of magnetic configurations can be used, the most basic distinction being between mirror confinement and toroidal confinement, especially tokamaks and stellarators.
Inertial
A third confinement principle is to apply a rapid pulse of energy to a large part of the surface of a pellet of fusion fuel, causing it to simultaneously "implode" and heat to very high pressure and temperature. If the fuel is dense enough and hot enough, the fusion reaction rate will be high enough to burn a significant fraction of the fuel before it has dissipated. To achieve these extreme conditions, the initially cold fuel must be explosively compressed. Inertial confinement is used in the hydrogen bomb, where the driver is x-rays created by a fission bomb. Inertial confinement is also attempted in "controlled" nuclear fusion, where the driver is a laser, ion, or electron beam, or a Z-pinch.
Some other confinement principles have been investigated, such as muon-catalyzed fusion, the Farnsworth-Hirsch fusor and Polywell (inertial electrostatic confinement), and bubble fusion.
Production methods
A variety of methods are known to effect nuclear fusion. Some are "cold" in the strict sense that no part of the material is hot (except for the reaction products), some are "cold" in the limited sense that the bulk of the material is at a relatively low temperature and pressure but the reactants are not, and some are "hot" fusion methods that create macroscopic regions of very high temperature and pressure.
Locally cold fusion
- Muon-catalyzed fusion is a well-established and reproducible fusion process that occurs at ordinary temperatures. It was studied in detail by Steven Jones in the early 1980s. It has not been reported to produce net energy. Net energy production from this reaction is not believed to be possible because of the energy required to create muons, their 2.2¬†¬Ķs half-life, and the chance that a muon will bind to the new alpha particle and thus stop catalyzing fusion.
Generally cold, locally hot fusion
- Accelerator based light-ion fusion. Using particle accelerators it is possible to achieve particle kinetic energies sufficient to induce many light ion fusion reactions. Of particular relevance into this discussion are devices referred to as sealed-tube neutron generators. These small devices are miniature particle accelerators filled with deuterium and tritium gas in an arrangement which allows ions of these nuclei to be accelerated against hydride targets, also containing deuterium and tritium, where fusion takes place. Hundreds of neutron generators are produced annually for use in the petroleum industry where they are used in measurement equipment for locating and mapping oil reserves. Despite periodic reports in the popular press by scientists claiming to have invented "table-top" fusion machines, neutron generators have been around for half a century. The sizes of these devices vary but the smallest instruments are often packaged in sizes smaller than a loaf of bread. These devices do not produce a net power output.
- In sonoluminescence, acoustic shock waves create temporary bubbles that collapse shortly after creation, producing very high temperatures and pressures. In 2002, Rusi P. Taleyarkhan reported the possibility that bubble fusion occurs in those collapsing bubbles (sonofusion). As of 2005, experiments to determine whether fusion is occurring give conflicting results. If fusion is occurring, it is because the local temperature and pressure are sufficiently high to produce hot fusion.[2]
- The Farnsworth-Hirsch Fusor is a tabletop device in which fusion occurs. This fusion comes from high effective temperatures produced by electrostatic acceleration of ions. The device can be built inexpensively, but it too is unable to produce a net power output.
- Antimatter-initialized fusion uses small amounts of antimatter to trigger a tiny fusion explosion. This has been studied primarily in the context of making nuclear pulse propulsion feasible. This is not near becoming a practical power source, due to the cost of manufacturing antimatter alone.
- Pyroelectric fusion was reported in April 2005 by a team at UCLA. The scientists used a pyroelectric crystal heated from ‚ąí34 to 7 ¬įC (‚ąí30 to 45 ¬įF), combined with a tungsten needle to produce an electric field of about 25¬†gigavolts per meter to ionize and accelerate deuterium nuclei into an erbium deuteride target. Though the energy of the deuterium ions generated by the crystal has not been directly measured, the authors used 100¬†keV (a temperature of about 109¬†K) as an estimate in their modeling.[3] At these energy levels, two deuterium nuclei can fuse together to produce a helium-3 nucleus, a 2.45¬†MeV neutron and bremsstrahlung. Although it makes a useful neutron generator, the apparatus is not intended for power generation since it requires far more energy than it produces.[4][5][6]
Hot fusion
- "Standard" "hot" fusion, in which the fuel reaches tremendous temperature and pressure inside a fusion reactor or nuclear weapon.
The methods in the second group are examples of non-equilibrium systems, in which very high temperatures and pressures are produced in a relatively small region adjacent to material of much lower temperature. In his doctoral thesis for MIT, Todd Rider did a theoretical study of all quasineutral, isotropic, non-equilibrium fusion systems. He demonstrated that all such systems will leak energy at a rapid rate due to bremsstrahlung, radiation produced when electrons in the plasma hit other electrons or ions at a cooler temperature and suddenly decelerate. The problem is not as pronounced in a hot plasma because the range of temperatures, and thus the magnitude of the deceleration, is much lower. Note that Rider's work does not apply to non-neutral and/or anisotropic non-equilibrium plasmas.
Important reactions
Astrophysical reaction chains
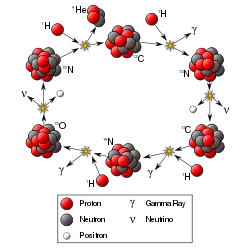
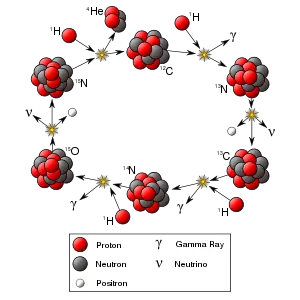
The most important fusion process in nature is that which powers the stars. The net result is the fusion of four protons into one alpha particle, with the release of two positrons, two neutrinos (which changes two of the protons into neutrons), and energy, but several individual reactions are involved, depending on the mass of the star. For stars the size of the sun or smaller, the proton-proton chain dominates. In heavier stars, the CNO cycle is more important. Both types of processes are responsible for the creation of new elements as part of stellar nucleosynthesis.
At the temperatures and densities in stellar cores the rates of fusion reactions are notoriously slow. For example, at solar core temperature (T ~ 15¬†MK) and density (~120¬†g/cm3), the energy release rate is only ~0.1¬†microwatt/cm3‚ÄĒmillions of times less than the rate of energy release of ordinary candela and thousands of times less than the rate at which a human body generates heat. Thus, reproduction of stellar core conditions in a lab for nuclear fusion power production is completely impractical. Because nuclear reaction rates strongly depend on temperature (~exp(-E/kT)), then in order to achieve reasonable rates of energy production in terrestrial fusion reactors 10‚Äď100 times higher temperatures (compared to stellar interiors) are required T~0.1‚Äď1.0 GK.
Criteria and candidates for terrestrial reactions
In man-made fusion, the primary fuel is not constrained to be protons and higher temperatures can be used, so reactions with larger cross-sections are chosen. This implies a lower Lawson criterion, and therefore less startup effort. Another concern is the production of neutrons, which activate the reactor structure radiologically, but also have the advantages of allowing volumetric extraction of the fusion energy and tritium breeding. Reactions that release no neutrons are referred to as aneutronic.
In order to be useful as a source of energy, a fusion reaction must satisfy several criteria. It must
- be exothermic: This may be obvious, but it limits the reactants to the low Z (number of protons) side of the curve of binding energy. It also makes helium-4 the most common product because of its extraordinarily tight binding, although He-3 and H-3 also show up;
- involve low Z nuclei: This is because the electrostatic repulsion must be overcome before the nuclei are close enough to fuse;
- have two reactants: At anything less than stellar densities, three body collisions are too improbable. It should be noted that in inertial confinement, both stellar densities and temperatures are exceeded to compensate for the shortcomings of the third parameter of the Lawson criterion, ICF's very short confinement time;
- have two or more products: This allows simultaneous conservation of energy and momentum without relying on the electromagnetic force;
- conserve both protons and neutrons: The cross sections for the weak interaction are too small.
Few reactions meet these criteria. The following are those with the largest cross sections:
| (1) | D | + | T | → |   | 4He | (3.5 MeV) | + |   | n | (14.1 MeV) |   | ||||
| (2i) | D | + | D | → |   | T | (1.01 MeV) | + |   | p | (3.02 MeV) |   |   |   |   | 50% |
| (2ii) |   |   |   | → |   | 3He | (0.82 MeV) | + |   | n | (2.45 MeV) |   |   |   |   | 50% |
| (3) | D | + | 3He | → |   | 4He | (3.6 MeV) | + |   | p | (14.7 MeV) | |||||
| (4) | T | + | T | → |   | 4He |   | + | 2  | n | + 11.3 MeV | |||||
| (5) | 3He | + | 3He | → |   | 4He |   | + | 2  | p | + 12.9 MeV | |||||
| (6i) | 3He | + | T | → |   | 4He |   | + |   | p |   | + | n | + 12.1 MeV |   | 51% |
| (6ii) |   |   |   | → |   | 4He | (4.8 MeV) | + |   | D | (9.5 MeV) |   |   |   |   | 43% |
| (6iii) |   |   |   | → |   | 4He | (0.5 MeV) | + |   | n | (1.9 MeV) | + | p | (11.9 MeV) |   | 6% |
| (7i) | D | + | 6Li | → | 2  | 4He | + 22.4 MeV |   |   |   |   |   |   |   |   | __% |
| (7ii) |   |   |   | → |   | 3He |   | + |   | 4He |   | + | n | + 2.56 MeV |   | __% |
| (7iii) |   |   |   | → |   | 7Li |   | + |   | p | + 5.0 MeV |   |   |   |   | __% |
| (7iv) |   |   |   | → |   | 7Be |   | + |   | n | + 3.4 MeV |   |   |   |   | __% |
| (8) | p | + | 6Li | → |   | 4He | (1.7 MeV) | + |   | 3He | (2.3 MeV) | |||||
| (9) | 3He | + | 6Li | → | 2  | 4He |   | + |   | p | + 16.9 MeV | |||||
| (10) | p | + | 11B | → | 3  | 4He | + | 8.7 MeV |
Note: p (protium), D (deuterium), and T (tritium) are shorthand notation for the main three isotopes of hydrogen.
For reactions with two products, the energy is divided between them in inverse proportion to their masses, as shown. In most reactions with three products, the distribution of energy varies. For reactions that can result in more than one set of products, the branching ratios are given.
Some reaction candidates can be eliminated at once. The D-6Li reaction has no advantage compared to p-11B because it is roughly as difficult to burn but produces substantially more neutrons through D-D side reactions. There is also a p-7Li reaction, but the cross section is far too low, except possibly when Ti > 1 MeV, but at such high temperatures an endothermic, direct neutron-producing reaction also becomes very significant. Finally there is also a p-9Be reaction, which is not only difficult to burn, but 9Be can be easily induced to split into two alphas and a neutron.
In addition to the fusion reactions, the following reactions with neutrons are important in order to "breed" tritium in "dry" fusion bombs and some proposed fusion reactors:
- n + 6Li ‚Üí T + 4He
- n + 7Li ‚Üí T + 4He + n
To evaluate the usefulness of these reactions, in addition to the reactants, the products, and the energy released, one needs to know something about the cross section. Any given fusion device will have a maximum plasma pressure that it can sustain, and an economical device will always operate near this maximum. Given this pressure, the largest fusion output is obtained when the temperature is chosen so that <ŌÉv>/T¬≤ is a maximum. This is also the temperature at which the value of the triple product nTŌĄ required for ignition is a minimum (a plasma is "ignited" if the fusion reactions produce enough power to maintain the temperature without external heating). This optimum temperature and the value of <ŌÉv>/T¬≤ at that temperature is given for a few of these reactions in the following table.
| fuel | T [keV] | <ŌÉv>/T¬≤ [m¬≥/s/keV¬≤] |
|---|---|---|
| D-T | 13.6 | 1.24√ó10-24 |
| D-D | 15 | 1.28√ó10-26 |
| D-3He | 58 | 2.24√ó10-26 |
| p-6Li | 66 | 1.46√ó10-27 |
| p-11B | 123 | 3.01√ó10-27 |
Note that many of the reactions form chains. For instance, a reactor fueled with T and 3He will create some D, which is then possible to use in the D + 3He reaction if the energies are "right." An elegant idea is to combine the reactions (8) and (9). The 3He from reaction (8) can react with 6Li in reaction (9) before completely thermalizing. This produces an energetic proton which in turn undergoes reaction (8) before thermalizing. A detailed analysis shows that this idea will not really work well, but it is a good example of a case where the usual assumption of a Maxwellian plasma is not appropriate.
Neutronicity, confinement requirement, and power density
Any of the reactions above can in principle be the basis of fusion power production. In addition to the temperature and cross section discussed above, we must consider the total energy of the fusion products Efus, the energy of the charged fusion products Ech, and the atomic number Z of the non-hydrogenic reactant.
Specification of the D-D reaction entails some difficulties, though. To begin with, one must average over the two branches (2) and (3). More difficult is to decide how to treat the T and 3He products. T burns so well in a deuterium plasma that it is almost impossible to extract from the plasma. The D-3He reaction is optimized at a much higher temperature, so the burnup at the optimum D-D temperature may be low, so it seems reasonable to assume the T but not the 3He gets burned up and adds its energy to the net reaction. Thus we will count the DD fusion energy as Efus = (4.03+17.6+3.27)/2 = 12.5 MeV and the energy in charged particles as Ech = (4.03+3.5+0.82)/2 = 4.2 MeV.
Another unique aspect of the D-D reaction is that there is only one reactant, which must be taken into account when calculating the reaction rate.
With this choice, we tabulate parameters for four of the most important reactions.
| fuel | Z | Efus [MeV] | Ech [MeV] | neutronicity |
|---|---|---|---|---|
| D-T | 1 | 17.6 | 3.5 | 0.80 |
| D-D | 1 | 12.5 | 4.2 | 0.66 |
| D-3He | 2 | 18.3 | 18.3 | ~0.05 |
| p-11B | 5 | 8.7 | 8.7 | ~0.001 |
The last column is the neutronicity of the reaction, the fraction of the fusion energy released as neutrons. This is an important indicator of the magnitude of the problems associated with neutrons like radiation damage, biological shielding, remote handling, and safety. For the first two reactions it is calculated as (Efus-Ech)/Efus. For the last two reactions, where this calculation would give zero, the values quoted are rough estimates based on side reactions that produce neutrons in a plasma in thermal equilibrium.
Of course, the reactants should also be mixed in the optimal proportions. This is the case when each reactant ion plus its associated electrons accounts for half the pressure. Assuming that the total pressure is fixed, this means that density of the non-hydrogenic ion is smaller than that of the hydrogenic ion by a factor 2/(Z+1). Therefore the rate for these reactions is reduced by the same factor, on top of any differences in the values of <ŌÉv>/T¬≤. On the other hand, because the D-D reaction has only one reactant, the rate is twice as high as if the fuel were divided between two hydrogenic species.
Thus there is a "penalty" of (2/(Z+1)) for non-hydrogenic fuels arising from the fact that they require more electrons, which take up pressure without participating in the fusion reaction (It is usually a good assumption that the electron temperature will be nearly equal to the ion temperature. Some authors, however, discuss the possibility that the electrons could be maintained substantially colder than the ions. In such a case, known as a "hot ion mode," the "penalty" would not apply. There is at the same time a "bonus" of a factor 2 for D-D due to the fact that each ion can react with any of the other ions, not just a fraction of them.
We can now compare these reactions in the following table:
| fuel | <ŌÉv>/T¬≤ | penalty/bonus | reactivity | Lawson criterion | power density |
|---|---|---|---|---|---|
| D-T | 1.24√ó10-24 | 1 | 1 | 1 | 1 |
| D-D | 1.28√ó10-26 | 2 | 48 | 30 | 68 |
| D-3He | 2.24√ó10-26 | 2/3 | 83 | 16 | 80 |
| p-11B | 3.01√ó10-27 | 1/3 | 1240 | 500 | 2500 |
The maximum value of <ŌÉv>/T2 is taken from a previous table. The "penalty/bonus" factor is that related to a non-hydrogenic reactant or a single-species reaction. The values in the column "reactivity" are found by dividing 1.24√ó10-24 by the product of the second and third columns. It indicates the factor by which the other reactions occur more slowly than the D-T reaction under comparable conditions. The column "Lawson criterion" weights these results with Ech and gives an indication of how much more difficult it is to achieve ignition with these reactions, relative to the difficulty for the D-T reaction. The last column is labeled "power density" and weights the practical reactivity with Efus. It indicates how much lower the fusion power density of the other reactions is compared to the D-T reaction and can be considered a measure of the economic potential.
Bremsstrahlung losses in quasineutral, isotropic plasmas
The ions undergoing fusion in many systems will essentially never occur alone but will be mixed with electrons that in aggregate neutralize the ions' bulk electrical charge and form a plasma. The electrons will generally have a temperature comparable to or greater than that of the ions, so they will collide with the ions and emit x-ray radiation of 10‚Äď30 keV energy (Bremsstrahlung). The sun and stars are opaque to x-rays, but essentially any terrestrial fusion reactor will be optically thin for x-rays of this energy range. X-rays are difficult to reflect but they are effectively absorbed (and converted into heat) in less than mm thickness of stainless steel (which is part of reactor shield). The ratio of fusion power produced to x-ray radiation lost to walls is an important figure of merit. This ratio is generally maximized at a much higher temperature than that which maximizes the power density (see the previous subsection). The following table shows the rough optimum temperature and the power ratio at that temperature for several reactions.
| fuel | Ti (keV) | Pfusion/PBremsstrahlung |
|---|---|---|
| D-T | 50 | 140 |
| D-D | 500 | 2.9 |
| D-3He | 100 | 5.3 |
| 3He-3He | 1000 | 0.72 |
| p-6Li | 800 | 0.21 |
| p-11B | 300 | 0.57 |
The actual ratios of fusion to Bremsstrahlung power will likely be significantly lower for several reasons. For one, the calculation assumes that the energy of the fusion products is transmitted completely to the fuel ions, which then lose energy to the electrons by collisions, which in turn lose energy by Bremsstrahlung. However because the fusion products move much faster than the fuel ions, they will give up a significant fraction of their energy directly to the electrons. Secondly, the plasma is assumed to be composed purely of fuel ions. In practice, there will be a significant proportion of impurity ions, which will lower the ratio. In particular, the fusion products themselves must remain in the plasma until they have given up their energy, and will remain some time after that in any proposed confinement scheme. Finally, all channels of energy loss other than Bremsstrahlung have been neglected. The last two factors are related. On theoretical and experimental grounds, particle and energy confinement seem to be closely related. In a confinement scheme that does a good job of retaining energy, fusion products will build up. If the fusion products are efficiently ejected, then energy confinement will be poor, too.
The temperatures maximizing the fusion power compared to the Bremsstrahlung are in every case higher than the temperature that maximizes the power density and minimizes the required value of the fusion triple product. This will not change the optimum operating point for D-T very much because the Bremsstrahlung fraction is low, but it will push the other fuels into regimes where the power density relative to D-T is even lower and the required confinement even more difficult to achieve. For D-D and D-3He, Bremsstrahlung losses will be a serious, possibly prohibitive problem. For 3He-3He, p-6Li and p-11B the Bremsstrahlung losses appear to make a fusion reactor using these fuels with a quasineutral, anisotropic plasma impossible. Some ways out of this dilemma are considered‚ÄĒand rejected‚ÄĒin ‚ÄúFundamental limitations on plasma fusion systems not in thermodynamic equilibrium‚ÄĚ by Todd Rider.[7] This limitation does not apply to non-neutral and anisotropic plasmas; however, these have their own challenges to contend with.
See also
Notes
- ‚ÜĎ Carl R. Nave, ‚ÄúThe Most Tightly Bound Nuclei,‚ÄĚ HyperPhysics. Retrieved February 6, 2017.
- ‚ÜĎ ‚ÄúDesktop fusion is back on the table,‚ÄĚ Nature.com. Retrieved February 6,2017.
- ‚ÜĎ ‚ÄúSupplementary methods for ‚ÄúObservation of nuclear fusion driven by a pyroelectric crystal,‚ÄĚ Nature.com. Retrieved February 6, 2017.
- ‚ÜĎ B. Naranjo, J. K. Gimzewski and S. Putterman, ‚ÄúObservation of nuclear fusion driven by a pyroelectric crystal,‚ÄĚ UCLA (2005). Retrieved February 6, 2017.
- ‚ÜĎ Michelle Thaller, ‚ÄúComing in out of the cold: Cold fusion, for real,‚ÄĚ Christian Science Monitor (June 6, 2005). Retrieved February 6, 2017.
- ‚ÜĎ ‚ÄúNuclear fusion on the desktop ... really!‚ÄĚ MSNBC.com (April 27, 2005). Retrieved February 6, 2017.
- ‚ÜĎ Todd Rider, ‚ÄúFundamental limitations on plasma fusion systems not in thermodynamic equilibrium‚ÄĚ Ph.D. thesis, Massachusetts Institute of Technology. Abstract available online. Retrieved February 6, 2017.
ReferencesISBN links support NWE through referral fees
- Krane, Kenneth S. and David Halliday. Introductory Nuclear Physics. New York: Wiley, 1988. ISBN 047180553X
- Martin, Brian. Nuclear and Particle Physics: An Introduction. Hoboken, NJ: Wiley, 2006. ISBN 0470025328
- Poenaru, D. N. Nuclear Decay Modes. Fundamental and Applied Nuclear Physics Series. Philadelphia, PA: Institute of Physics, 1996. ISBN 0750303387
- Tipler, Paul and Ralph Llewellyn. Modern Physics. 4th ed. New York: W.H. Freeman, 2002. ISBN 0716743450
External links
All links retrieved November 16, 2022.
- Fusion Power Associates
- ‚ÄúResearch Uses Sonofusion to Generate Temperatures Hot Enough For Fusion‚ÄĚ by Kenneth Chang, The New York Times ‚Äď MIT
- Nuclear Fusion Animation ‚Äď Atomic Archive.com
- Nuclear Fusion Explained ‚Äď Atomic Archive.com
- ‚ÄúChaos could keep fusion under control‚ÄĚ by Geoff Brumfiel, Nature
| Nuclear technology | |
|---|---|
| Nuclear engineering | Nuclear physics | Nuclear fission | Nuclear fusion | Radiation | Ionizing radiation | Atomic nucleus | Nuclear reactor | Nuclear safety |
| Nuclear material | Nuclear fuel | Fertile material | Thorium | Uranium | Enriched uranium | Depleted uranium | Plutonium |
| Nuclear power | Nuclear power plant | Radioactive waste | Fusion power | Future energy development | Inertial fusion power plant | Pressurized water reactor | Boiling water reactor | Generation IV reactor | Fast breeder reactor | Fast neutron reactor | Magnox reactor | Advanced gas-cooled reactor | Gas-cooled fast reactor | Molten salt reactor | Liquid-metal-cooled reactor | Lead-cooled fast reactor | Sodium-cooled fast reactor | Supercritical water reactor | Very high temperature reactor | Pebble bed reactor | Integral Fast Reactor | Nuclear propulsion | Nuclear thermal rocket | Radioisotope thermoelectric generator |
| Nuclear medicine | PET | Radiation therapy | Tomotherapy | Proton therapy | Brachytherapy |
| Nuclear weapons | History of nuclear weapons | Nuclear warfare | Nuclear arms race | Nuclear weapon design | Effects of nuclear explosions | Nuclear testing | Nuclear delivery | Nuclear proliferation | List of states with nuclear weapons | List of nuclear tests |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.