Nuclear reactor

This article elaborates on the central technology of generating nuclear power.

Core of CROCUS, a small nuclear reactor used for research at the EPFL in Switzerland.

A nuclear reactor is a device in which nuclear chain reactions are initiated, controlled, and sustained at a steady rate, as opposed to a nuclear bomb, in which the chain reaction occurs in a fraction of a second and is uncontrolled causing an explosion.

The most significant use of nuclear reactors is as an energy source for the generation of electrical power (see Nuclear power) and for the power in some ships (see Nuclear marine propulsion). This is usually accomplished by methods that involve using heat from the nuclear reaction to power steam turbines. There are also other less common uses as discussed below.

How it works

An induced nuclear fission event. A neutron is absorbed by the nucleus of a uranium-235 atom, which in turn splits into fast-moving lighter elements (fission products) and free neutrons.

The physics of operating a nuclear reactor are explained in Nuclear reactor physics.

Just as many conventional thermal power stations generate electricity by harnessing the thermal energy released from burning fossil fuels, nuclear power plants convert the thermal energy released from nuclear fission.

Reactor

The reactor is used to convert atomic energy into heat. While a reactor could be one in which heat is produced by fusion or radioactive decay, this description focuses on the basic principles of the fission reactor.

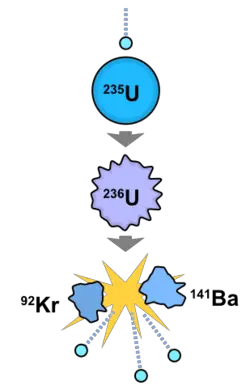
Fission

When a relatively large fissile atomic nucleus (usually uranium-235 or plutonium-239) absorbs a neutron it is likely to undergo nuclear fission. The atom splits into two or more smaller nuclei with kinetic energy (known as fission products) and also releases gamma radiation and free neutrons. A portion of these neutrons may later be absorbed by other fissile atoms and create more fissions, which release more neutrons, and so on.

The nuclear chain reaction can be controlled by using neutron poisons and neutron moderators to change the portion of neutrons that will go on to cause more fissions.* Increasing or decreasing the rate of fission will also increase or decrease the energy output of the reactor.

Heat generation

The reactor core generates heat in a number of ways:

• The kinetic energy of fission products is converted to thermal energy when these nuclei collide with nearby atoms
• Some of the gamma rays produced during fission are absorbed by the reactor in the form of heat
• Heat produced by the radioactive decay of fission products and materials that have been activated by neutron absorption. This decay heat source will remain for some time even after the reactor is shutdown

Cooling

A cooling source—often water but sometimes a liquid metal—is circulated past the reactor core to absorb the heat that it generates. The heat is carried away from the reactor and is then used to generate steam. Most reactor systems employ a cooling system that is physically separate from the water that will be boiled to produce pressurized steam for the turbines, but in some reactors the water for the steam turbines is boiled directly by the reactor core.

Reactivity control

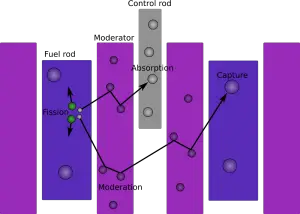
The power output of the reactor is controlled by controlling how many neutrons are able to create more fissions.

Control rods that are made of a nuclear poison are used to absorb neutrons. Absorbing more neutrons in a control rod means that there are fewer neutrons available to cause fission, so pushing the control rod deeper into the reactor will reduce it's power output, and extracting the control rod will increase it.

In some reactors, the coolant also acts as a neutron moderator. A moderator increases the power of the reactor by causing the fast neutrons that are released from fission to lose energy and become thermal neutrons. Thermal neutrons are more likely than fast neutrons to cause fission, so more neutron moderation means more power output from the reactors. If the coolant is a moderator, then temperature changes can affect the density of the coolant/moderator and therefore change power output. A higher temperature coolant would be less dense, and therefore a less effective moderator.

In other reactors the coolant acts as a poison by absorbing neutrons in the same way that the control rods do. In these reactors power output can be increased by heating the coolant, which makes it a less dense poison.

Nuclear reactors generally have automatic and manual systems to insert large amounts of poison into the reactor to shut the fission reaction down if unsafe conditions are detected.

Electrical power generation

The energy released in the fission process generates heat, some of which can be converted into usable energy. A common method of harnessing this thermal energy is to use it to boil water to produce pressurized steam which will then drive a steam turbine that generates electricity.

Components

The control room of NC State's Pulstar Nuclear Reactor.

The key components common to most types of nuclear power plants are:

• Nuclear fuel
• Nuclear reactor core
• Neutron moderator
• Neutron poison
• Coolant (often the Neutron Moderator and the Coolant are the same, usually both purified water)
• Control rods
• Reactor vessel
• Boiler feedwater pump
• Steam generators (not in BWRs)
• Steam turbine
• Electrical generator
• Condenser
• Cooling tower (not always required)
• Radwaste System (a section of the plant handling radioactive waste)
• Refueling Floor
• Spent fuel pool
• Reactor Protective System (RPS)
• Emergency Core Cooling Systems (ECCS)
• Standby Liquid Control System (emergency boron injection, in BWRs only)
• Containment building
• Control room
• Emergency Operations Facility

The people in a nuclear power plant

Nuclear power plants typically employ just under a thousand people per reactor (including security guards and engineers associated with the plant but working elsewhere).

• Nuclear engineers
• Reactor operators
• Health physicists

In the United States and Canada, all non-management and non-security workers are members of the International Brotherhood of Electrical Workers.

Reactor types

NC State's PULSTAR Reactor is a 1 MW pool-type research reactor with 4 percent enriched, pin-type fuel consisting of UO₂ pellets in zircaloy cladding.

Classifications

Nuclear Reactors are classified by several methods; a brief outline of these classification schemes is provided.

Classification by type of nuclear reaction

• Nuclear fission. Most reactors, and all commercial ones, are based on nuclear fission. They generally use uranium as fuel, but research on using thorium is ongoing (an example is the liquid fluoride reactor). This article assumes that the technology is nuclear fission unless otherwise stated. Fission reactors can be divided roughly into two classes, depending on the energy of the neutrons that are used to sustain the fission chain reaction:
  • Thermal reactors use slow or thermal neutrons. Most power reactors are of this type. These are characterized by neutron moderator materials that slow neutrons until they approach the average kinetic energy of the surrounding particles, that is, until they are thermalized. Thermal neutrons have a far higher probability of fissioning uranium-235, and a lower probability of capture by uranium-238 than the faster neutrons that result from fission. As well as the moderator, thermal reactors have fuel (fissionable material), containments, pressure vessels, shielding, and instrumentation to monitor and control the reactor's systems.
  • Fast neutron reactors use fast neutrons to sustain the fission chain reaction. They are characterized by an absence of moderating material. Initiating the chain reaction requires enriched uranium (and/or enrichment with plutonium 239), due to the lower probability of fissioning U-235, and a higher probability of capture by U-238 (as compared to a moderated, thermal neutron). Fast reactors have the potential to produce less transuranic waste because all actinides are fissionable with fast neutrons, but they are more difficult to build and more expensive to operate. Overall, fast reactors are less common than thermal reactors in most applications. Some early power stations were fast reactors, as are some Russian naval propulsion units. Construction of prototypes is continuing (see fast breeder or generation IV reactors).
• Nuclear fusion. Fusion power is an experimental technology, generally with hydrogen as fuel. While not currently suitable for power production, Farnsworth-Hirsch fusors are used to produce neutron radiation.
• Radioactive decay. Examples include radioisotope thermoelectric generators and atomic batteries, which generate heat and power by exploiting passive radioactive decay.

Classification by moderator material

Used by thermal reactors:

• Graphite moderated reactors
• Water moderated reactors
  • Heavy water reactors
  • Light water moderated reactors (LWRs). Light water reactors use ordinary water to moderate and cool the reactors. When at operating temperatures if the temperature of the water increases, its density drops, and fewer neutrons passing through it are slowed enough to trigger further reactions. That negative feedback stabilizes the reaction rate. Graphite and heavy water reactors tend to be more thoroughly thermalized than light water reactors. Due to the extra thermalization, these types can use natural uranium/unenriched fuel.
• Light element moderated reactors. These reactors are moderated by lithium or beryllium.
  • Molten salt reactors (MSRs) are moderated by a light elements such as lithium or beryllium, which are constituents of the coolant/fuel matrix salts LiF and BeF₂.
  • Liquid metal cooled reactors, such as one whose coolant in a mixture of Lead and Bismuth, may use BeO as a moderator.
• Organically moderated reactors (OMR) use biphenyl and terphenyl as moderator and coolant.

Classification by coolant

In thermal nuclear reactors (LWRs in specific), the coolant acts as a moderator that must slow down the neutrons before they can be efficiently absorbed by the fuel.

• Water cooled reactor
  • Pressurized water reactor (PWR)
    • A primary characteristic of PWRs is a pressurizer, a specialized pressure vessel. Most commercial PWRs and naval reactors use pressurizers. During normal operation, a pressurizer is partially filled with water, and a steam bubble is maintained above it by heating the water with submerged heaters. During normal operation, the pressurizer is connected to the primary reactor pressure vessel (RPV) and the pressurizer "bubble" provides an expansion space for changes in water volume in the reactor. This arrangement also provides a means of pressure control for the reactor by increasing or decreasing the steam pressure in the pressurizer using the pressurizer heaters.
    • Pressurized channels. Channel-type reactors can be refueled under load.
  • Boiling water reactor (BWR)
    • BWRs are characterized by boiling water around the fuel rods in the lower portion of primary reactor pressure vessel. During normal operation, pressure control is accomplished by controlling the amount of steam flowing from the reactor pressure vessel to the turbine.
  • Pool-type reactor
• Liquid metal cooled reactor. Since water is a moderator, it cannot be used as a coolant in a fast reactor. Liquid metal coolants have included sodium, NaK, lead, lead-bismuth eutectic, and in early reactors, mercury.
  • Sodium-cooled fast reactor
  • Lead-cooled fast reactor
• Gas cooled reactors are cooled by a circulating inert gas, usually helium. Nitrogen and carbon dioxide have also been used. Utilization of the heat varies, depending on the reactor. Some reactors run hot enough that the gas can directly power a gas turbine. Older designs usually run the gas through a heat exchanger to make steam for a steam turbine.
• Molten Salt Reactors (MSRs) are cooled by circulating a molten salt, typically a eutectic mixture of fluoride salts, such as LiF and BeF2. In a typical MSR, the coolant is also used a matrix in which the fissile material is dissolved.

Classification by generation

• Generation I reactor
• Generation II reactor
• Generation III reactor
• Generation IV reactor

The "Gen IV"-term was dubbed by the DOE for developing new plant types in 2000. In 2003, the French CEA was the first to refer to Gen II types in Nucleonics Week; "Etienne Pochon, CEA director of nuclear industry support, outlined EPR's improved performance and enhanced safety features compared to the advanced Generation II designs on which it was based." First mentioning of Gen III was also in 2000 in conjunction with the launch of the GIF plans.

Classification by phase of fuel

• Solid fueled
• Fluid fueled
• Gas fueled

Classification by use

• Electricity
  • Nuclear power plants
• Propulsion, see nuclear propulsion
  • Nuclear marine propulsion
  • Various proposed forms of rocket propulsion
• Other uses of heat
  • Desalination
  • Heat for domestic and industrial heating
  • Hydrogen production for use in a hydrogen economy
• Production reactors for transmutation of elements
  • Breeder reactors. Fast breeder reactors are capable of enriching Uranium during the fission chain reaction (by converting fertile U-238 to Pu-239) which allows an operational fast reactor to generate more fissile material than it consumes. Thus, a breeder reactor, once running, can be re-fueled with natural or even depleted uranium.
    
  • Creating various radioactive isotopes, such as americium for use in smoke detectors, and cobalt-60, molybdenum-99 and others, used for imaging and medical treatment.
  • Production of materials for nuclear weapons such as weapons-grade plutonium
• Providing a source of neutron radiation (for example with the pulsed Godiva device) and positron radiation) (for example, neutron activation analysis and potassium-argon dating.
• Research reactor: Typically reactors used for research and training, materials testing, or the production of radioisotopes for medicine and industry. These are much smaller than power reactors or those propelling ships, and many are on university campuses. There are about 280 such reactors operating, in 56 countries. Some operate with high-enriched uranium fuel, and international efforts are underway to substitute low-enriched fuel.

Current technologies

There are two types of nuclear power in current use:

• The Radioisotope thermoelectric generator
  • These systems produces heat through passive radioactive decay. Some radioisotope thermoelectric generators have been created to power space probes (for example, the Cassini probe), some lighthouses in the former Soviet Union, and some pacemakers. The heat output of these generators diminishes with time; the heat is converted to electricity utilizing the thermoelectric effect.
• Nuclear fission reactors
  • The nuclear fission reactor produces heat through a controlled nuclear chain reaction in a critical mass of fissile material. All current nuclear power plants are critical fission reactors, which are the focus of this article. The output of fission reactors is controllable. There are several subtypes of critical fission reactors, which can be classified as Generation I, Generation II and Generation III. All reactors will be compared to the Pressurized Water Reactor (PWR), as that is the standard modern reactor design.
    

    Diablo Canyon—a PWR
  • Pressurized Water Reactors (PWR)
    • These reactors use a pressure vessel to contain the nuclear fuel, control rods, moderator, and coolant. They are cooled and moderated by high pressure liquid water. The hot radioactive water that leaves the pressure vessel is looped through a steam generator, which in turn heats a secondary (non-radioactive) loop of water to steam that can run turbines. They are the majority of current reactors, and are generally considered the safest and most reliable technology currently in large scale deployment. This is a thermal neutron reactor design, the newest of which are the Advanced Pressurized Water Reactor and the European Pressurized Reactor. United States Naval reactors are of this type.

    

    Laguna Verde nuclear power plant - a BWR

  • Boiling Water Reactors (BWR)

    A BWR is like a PWR without the steam generator. A boiling water reactor is cooled and moderated by water like a PWR, but at a lower pressure, which allows the water to boil inside the pressure vessel producing the steam that runs the turbines. Unlike a PWR, there is no primary and secondary loop. The thermal efficiency of these reactors can be higher, and they can be simpler, and even potentially more stable and safe. This is a thermal neutron reactor design, the newest of which are the Advanced Boiling Water Reactor and the Economic Simplified Boiling Water Reactor.

    

    The CANDU Qinshan Nuclear Power Plant

  • Pressurized Heavy Water Reactor (PHWR)

    A Canadian design, (known as CANDU) these reactors are heavy-water-cooled and -moderated Pressurized-Water reactors. Instead of using a single large pressure vessel as in a PWR, the fuel is contained in hundreds of pressure tubes. These reactors are fueled with natural uranium and are thermal neutron reactor designs. PHWRs can be refueled while at full power, which makes them very efficient in their use of uranium (it allows for precise flux control in the core). CANDU PHWR's have been built in Canada, Argentina, China, India (pre-NPT), Pakistan (pre-NPT), Romania, and South Korea. India also operates a number of PHWR's, often termed 'CANDU-derivatives', built after the Government of Canada halted nuclear dealings with India following the 1974 Smiling Buddha nuclear weapon test.

    

    The Ignalina Nuclear Power Plant—a still operating RBMK

  • Reaktor Bolshoy Moshchnosti Kanalniy (High Power Channel Reactor) (RBMK)

    A Soviet Union design, built to produce plutonium as well as power. RBMKs are water cooled with a graphite moderator. RBMKs are in some respects similar to CANDU in that they are refuelable during power operation and employ a pressure tube design instead of a PWR-style pressure vessel. However, unlike CANDU they are very unstable and too large to have containment buildings, making them dangerous in the case of an accident. A series of critical safety flaws have also been identified with the RBMK design, though some of these were corrected following the Chernobyl accident. RBMK reactors are generally considered one of the most dangerous reactor designs in use. The Chernobyl plant had four RBMK reactors.

    

    The Torness nuclear power station—an AGR

  • Gas Cooled Reactor (GCR) and Advanced Gas Cooled Reactor (AGR)

    These are generally graphite moderated and CO₂ cooled. They can have a high thermal efficiency compared with PWRs due to higher operating temperatures. There are a number of operating reactors of this design, mostly in the United Kingdom, where the concept was developed. Older designs (that is, Magnox stations) are either shut down or will be in the near future. However, the AGCRs have an anticipated life of a further 10 to 20 years. This is a thermal neutron reactor design. Decommissioning costs can be high due to large volume of reactor core.

  • Liquid Metal Fast Breeder Reactor (LMFBR)

    This is a reactor design that is cooled by liquid metal, totally unmoderated, and produces more fuel than it consumes. They are said to "breed" fuel, because they produce fissionable fuel during operation because of neutron capture. These reactors can function much like a PWR in terms of efficiency, and do not require much high pressure containment, as the liquid metal does not need to be kept at high pressure, even at very high temperatures. Superphénix in France was a reactor of this type, as was Fermi-I in the United States. The Monju reactor in Japan suffered a sodium leak in 1995 and was approved for restart in 2008. All three use/used liquid sodium. These reactors are fast neutron, not thermal neutron designs. These reactors come in two types:

    

    The Superphenix, one of the few FBRs

    • Lead cooled

      Using lead as the liquid metal provides excellent radiation shielding, and allows for operation at very high temperatures. Also, lead is (mostly) transparent to neutrons, so fewer neutrons are lost in the coolant, and the coolant does not become radioactive. Unlike sodium, lead is mostly inert, so there is less risk of explosion or accident, but such large quantities of lead may be problematic from toxicology and disposal points of view. Often a reactor of this type would use a lead-bismuth eutectic mixture. In this case, the bismuth would present some minor radiation problems, as it is not quite as transparent to neutrons, and can be transmuted to a radioactive isotope more readily than lead.

    • Sodium cooled

      Most LMFBRs are of this type. The sodium is relatively easy to obtain and work with, and it also manages to actually prevent corrosion on the various reactor parts immersed in it. However, sodium explodes violently when exposed to water, so care must be taken, but such explosions wouldn't be vastly more violent than (for example) a leak of superheated fluid from a SCWR or PWR. EBR-I, the first reactor to have a core meltdown, was of this type.

  • Aqueous Homogeneous Reactor

Future and developing technologies

Advanced reactors

More than a dozen advanced reactor designs are in various stages of development. Some are evolutionary from the PWR, BWR and PHWR designs above, some are more radical departures. The former include the Advanced Boiling Water Reactor (ABWR), two of which are now operating with others under construction, and the planned passively safe ESBWR and AP1000 units (see Nuclear Power 2010 Program).

• The Integral Fast Reactor was built, tested and evaluated during the 1980s and then retired under the Clinton administration in the 1990s due to nuclear non-proliferation policies of the administration. Recycling spent fuel is the core of its design and it therefore produces only a fraction of the waste of current reactors.
• The Pebble Bed Reactor, a High Temperature Gas Cooled Reactor (HTGCR), is designed so high temperatures reduce power output by doppler broadening of the fuel's neutron cross-section. It uses ceramic fuels so its safe operating temperatures exceed the power-reduction temperature range. Most designs are cooled by inert helium. Helium is not subject to steam explosions, resists neutron absorption leading to radioactivity, and does not dissolve contaminants that can become radioactive. Typical designs have more layers (up to 7) of passive containment than light water reactors (usually 3). A unique feature that may aid safety is that the fuel-balls actually form the core's mechanism, and are replaced one-by-one as they age. The design of the fuel makes fuel reprocessing expensive.
• SSTAR, Small, Sealed, Transportable, Autonomous Reactor is being primarily researched and developed in the U.S., intended as a fast breeder reactor that is passively safe and could be remotely shut down in case the suspicion arises that it is being tampered with.
• The Clean And Environmentally Safe Advanced Reactor (CAESAR) is a nuclear reactor concept that uses steam as a moderator—this design is still in development.
• Subcritical reactors are designed to be safer and more stable, but pose a number of engineering and economic difficulties. One example is the Energy amplifier.
• Thorium based reactors. It is possible to convert Thorium-232 into U-233 in reactors specially designed for the purpose. In this way, Thorium, which is more plentiful than uranium, can be used to breed U-233 nuclear fuel. U-233 is also believed to have favorable nuclear properties as compared to traditionally used U-235, including better neutron economy and lower production of long lived transuranic waste.
  • Advanced Heavy Water Reactor—A proposed heavy water moderated nuclear power reactor that will be the next generation design of the PHWR type. Under development in the Bhabha Atomic Research Centre (BARC).
  • KAMINI—A unique reactor using Uranium-233 isotope for fuel. Built by BARC and IGCAR Uses thorium.
  • India is also building a bigger scale FBTR or fast breeder thorium reactor to harness the power with the use of thorium.

Generation IV reactors

Generation IV reactors are a set of theoretical nuclear reactor designs currently being researched. These designs are generally not expected to be available for commercial construction before 2030. Current reactors in operation around the world are generally considered second- or third-generation systems, with the first-generation systems having been retired some time ago. Research into these reactor types was officially started by the Generation IV International Forum (GIF) based on eight technology goals. The primary goals being to improve nuclear safety, improve proliferation resistance, minimize waste and natural resource utilization, and to decrease the cost to build and run such plants.

• Gas cooled fast reactor
• Lead cooled fast reactor
• Molten salt reactor
• Sodium-cooled fast reactor
• Supercritical water reactor
• Very high temperature reactor

Generation V+ reactors

Designs which are theoretically possible, but which are not being actively considered or researched at present. Though such reactors could be built with current or near term technology, they trigger little interest for reasons of economics, practicality, or safety.

• Liquid Core reactor. A closed loop liquid core nuclear reactor, where the fissile material is molten uranium cooled by a working gas pumped in through holes in the base of the containment vessel.
• Gas core reactor. A closed loop version of the nuclear lightbulb rocket, where the fissile material is gaseous uranium-hexafluoride contained in a fused silica vessel. A working gas (such as hydrogen) would flow around this vessel and absorb the UV light produced by the reaction. In theory, using UF₆ as a working fuel directly (rather than as a stage to one, as is done now) would mean lower processing costs, and very small reactors. In practice, running a reactor at such high power densities would probably produce unmanageable neutron flux.
• Gas core EM reactor. As in the Gas Core reactor, but with photovoltaic arrays converting the UV light directly to electricity.
• Fission fragment reactor

Fusion reactors

Controlled nuclear fusion could in principle be used in fusion power plants to produce power without the complexities of handling actinides, but significant scientific and technical obstacles remain. Several fusion reactors have been built, but as yet none has "produced" more thermal energy than electrical energy consumed. Despite research having started in the 1950s, no commercial fusion reactor is expected before 2050. The ITER project is currently leading the effort to commercialize fusion power.

Nuclear fuel cycle

Thermal reactors generally depend on refined and enriched uranium. Some nuclear reactors can operate with a mixture of plutonium and uranium (see MOX). The process by which uranium ore is mined, processed, enriched, used, possibly reprocessed and disposed of is known as the nuclear fuel cycle.

Under 1 percent of the uranium found in nature is the easily fissionable U-235 isotope and as a result most reactor designs require enriched fuel. Enrichment involves increasing the percentage of U-235 and is usually done by means of gaseous diffusion or gas centrifuge. The enriched result is then converted into uranium dioxide powder, which is pressed and fired into pellet form. These pellets are stacked into tubes which are then sealed and called fuel rods. Many of these fuel rods are used in each nuclear reactor.

Most BWR and PWR commercial reactors use uranium enriched to about 4% U-235, and some commercial reactors with a high neutron economy do not require the fuel to be enriched at all (that is, they can use natural uranium). According to the International Atomic Energy Agency there are at least 100 research reactors in the world fueled by highly enriched (weapons-grade/90 percent enrichment uranium). Theft risk of this fuel (potentially used in the production of a nuclear weapon) has led to campaigns advocating conversion of this type of reactor to low-enrichment uranium (which poses less threat of proliferation).

It should be noted that fissionable U-235 and non-fissionable U-238 are both used in the fission process. U-235 is fissionable by thermal (that is, slow-moving) neutrons. A thermal neutron is one which is moving about the same speed as the atoms around it. Since all atoms vibrate proportionally to their absolute temperature, a thermal neutron has the best opportunity to fission U-235 when it is moving at this same vibrational speed. On the other hand, U-238 is more likely to capture a neutron when the neutron is moving very fast. This U-239 atom will soon decay into plutonium-239, which is another fuel. Pu-239 is a viable fuel and must be accounted for even when a highly enriched uranium fuel is used. Plutonium fissions will dominate the U-235 fissions in some reactors, especially after the initial loading of U-235 is spent. Plutonium is fissionable with both fast and thermal neutrons, which make it ideal for either nuclear reactors or nuclear bombs.

Most reactor designs in existence are thermal reactors and typically use water as a neutron moderator (moderator means that it slows down the neutron to a thermal speed) and as a coolant. But in a fast breeder reactor, some other kind of coolant is used which will not moderate or slow the neutrons down much. This enables fast neutrons to dominate, which can effectively be used to constantly replenish the fuel supply. By merely placing cheap unenriched uranium into such a core, the non-fissionable U-238 will be turned into Pu-239, "breeding" fuel.

Fueling of nuclear reactors

The amount of energy in the reservoir of nuclear fuel is frequently expressed in terms of "full-power days," which is the number of 24-hour periods (days) a reactor is scheduled for operation at full power output for the generation of heat energy. The number of full-power days in a reactor's operating cycle (between refueling outage times) is related to the amount of fissile uranium-235 (U-235) contained in the fuel assemblies at the beginning of the cycle. A higher percentage of U-235 in the core at the beginning of a cycle will permit the reactor to be run for a greater number of full-power days.

At the end of the operating cycle, the fuel in some of the assemblies is "spent" and is discharged and replaced with new (fresh) fuel assemblies, although in practice it is the buildup of reaction poisons in nuclear fuel that determines the lifetime of nuclear fuel in a reactor. Long before all possible fission has taken place, the buildup of long-lived neutron absorbing fission byproducts impedes the chain reaction. The fraction of the reactor's fuel core replaced during refueling is typically one-fourth for a boiling-water reactor and one-third for a pressurized-water reactor.

Not all reactors need to be shut down for refueling; for example, pebble bed reactors, RBMK reactors, molten salt reactors, Magnox, AGR and CANDU reactors allow fuel to be shifted through the reactor while it is running. In a CANDU reactor, this also allows individual fuel elements to be situated within the reactor core that are best suited to the amount of U-235 in the fuel element.

The amount of energy extracted from nuclear fuel is called its "burn up," which is expressed in terms of the heat energy produced per initial unit of fuel weight. Burn up is commonly expressed as megawatt days thermal per metric ton of initial heavy metal.

History—early reactors

The first artificial nuclear reactor, Chicago Pile-1, was constructed at the University of Chicago by a team led by Enrico Fermi in 1942. It achieved criticality on December 2, 1942 at 3:25 p.m. The reactor support structure was made of wood, which supported a pile of graphite blocks, embedded in which was natural Uranium-oxide "pseudospheres," or "briquettes." Inspiration for such a reactor was provided by the discovery by Lise Meitner, Fritz Strassman and Otto Hahn in 1938 that bombardment of Uranium with neutrons (provided by an Alpha-on-Beryllium fusion reaction, a "neutron howitzer") produced a Barium residue, which they reasoned was created by the fissioning of the Uranium nuclei. Subsequent studies revealed that several neutrons were also released during the fissioning, making available the opportunity for a chain reaction. Shortly after the discovery of fission, Hitler's Germany invaded Poland in 1939, starting World War II in Europe, and all such research became militarily classified. On August 2, 1939, Albert Einstein wrote a letter to President Franklin D. Roosevelt suggesting that the discovery of Uranium's fission could lead to the development of "extremely powerful bombs of a new type," giving impetus to the study of reactors and fission.

Soon after the Chicago Pile, the U.S. military developed nuclear reactors for the Manhattan Project starting in 1943. The primary purpose for these reactors was the mass production of plutonium (primarily at the Hanford Site) for nuclear weapons. Fermi and Leo Szilard applied for a patent on reactors on 19 December, 1944. Its issuance was delayed for 10 years because of wartime secrecy.

"World's first nuclear power plant" is the claim made by signs at the site of the EBR-I, which is now a museum near Arco, Idaho. This experimental LMFBR operated by the U.S. Atomic Energy Commission produced 0.8 kW in a test on December 20, 1951 and 100 kW (electrical) the following day, having a design output of 200 kW (electrical).

Besides the military uses of nuclear reactors, there were political reasons to pursue civilian use of atomic energy. U.S. President Dwight Eisenhower made his famous Atoms for Peace speech to the UN General Assembly on December 8, 1953. This diplomacy led to the dissemination of reactor technology to U.S. institutions and worldwide.

The first nuclear power plant built for civil purposes was the AM-1 Obninsk Nuclear Power Plant, launched on June 27, 1954 in the Soviet Union. It produced around 5 MW (electrical).

After World War II, the U.S. military sought other uses for nuclear reactor technology. Research by the Army and the Air Force never came to fruition; however, the U.S. Navy succeeded when they steamed the USS Nautilus on nuclear power January 17, 1955.

The first commercial nuclear power station, Calder Hall in Sellafield, England was opened in 1956 with an initial capacity of 50 MW (later 200 MW)..

The first portable nuclear reactor "Alco PM-2A" used to generate electrical power (2 MW) for Camp century from 1960 .

Natural nuclear reactors

Although nuclear fission reactors are often thought of as being solely a product of modern technology, the first nuclear fission reactors were in fact naturally occurring. A natural nuclear fission reactor can occur under certain circumstances that mimic the conditions in a constructed reactor. Fifteen natural fission reactors have so far been found in three separate ore deposits at the Oklo mine in Gabon, West Africa. First discovered in 1972 by French physicist Francis Perrin, they are collectively known as the Oklo Fossil Reactors. Self-sustaining nuclear fission reactions took place in these reactors approximately 1.5 billion years ago, and ran for a few hundred thousand years, averaging 100 kW of power output during that time. The concept of a natural nuclear reactor was theorized as early as 1956 by Paul Kuroda at the University of Arkansas

Such reactors can no longer form on Earth: radioactive decay over this immense time span has reduced the proportion of U-235 in naturally occurring uranium to below the amount required to sustain a chain reaction.

The natural nuclear reactors formed when a uranium-rich mineral deposit became inundated with groundwater that acted as a neutron moderator, and a strong chain reaction took place. The water moderator would boil away as the reaction increased, slowing it back down again and preventing a meltdown. The fission reaction was sustained for hundreds of thousands of years.

These natural reactors are extensively studied by scientists interested in geologic radioactive waste disposal. They offer a case study of how radioactive isotopes migrate through the earth's crust. This is a significant area of controversy as opponents of geologic waste disposal fear that isotopes from stored waste could end up in water supplies or be carried into the environment.

See also

• Enrico Fermi
• Nuclear physics
• Nuclear power
• Radioactive decay
• Safety engineering

References

ISBN links support NWE through referral fees

• Bodansky, David. 2004. Nuclear Energy: Principles, Practices, and Prospects, 2nd ed. New York, NY: Springer. ISBN 0387207783.
• Cohen, Bernard L. 1990. The Nuclear Energy Option. New York, NY: Plenum Press. ISBN 9780306435676. Retrieved October 20, 2008.
• Kennesaw State University. 2005. An entry to nuclear power through an educational discussion of reactors. Nuclear Chemistry—Nuclear Reactors. Retrieved October 20, 2008.
• Murray, Raymond. 2001. Nuclear Energy: An Introduction to the Concepts, Systems, and Applications of Nuclear Processes, 5th ed. Oxford, UK: Butterworth-Heinemann. ISBN 075067136X.

External links

All links retrieved November 16, 2022.

• How Nuclear Power Works - Howstuffworks.com.
• Whyfiles.org - A road paved with pebbles.
• The Canadian Nuclear FAQ - a very information-rich resource about Canadian CANDU reactors.
• Freeview Video 'Nuclear Power Plants - What's the Problem' A Royal Institution Lecture by John Collier by the Vega Science Trust.
• SCK.CEN Belgian Nuclear Research Centre in Mol.
• American Nuclear Society - Glossary of Terms.
• Nuclear Energy Institute – How it Works: Electric Power Generation.
• The Georeactor Hypothesis.

---

Nuclear technology
Nuclear engineering	Nuclear physics | Nuclear fission | Nuclear fusion | Radiation | Ionizing radiation | Atomic nucleus | Nuclear reactor | Nuclear safety
Nuclear material	Nuclear fuel | Fertile material | Thorium | Uranium | Enriched uranium | Depleted uranium | Plutonium
Nuclear power	Nuclear power plant | Radioactive waste | Fusion power | Future energy development | Inertial fusion power plant | Pressurized water reactor | Boiling water reactor | Generation IV reactor | Fast breeder reactor | Fast neutron reactor | Magnox reactor | Advanced gas-cooled reactor | Gas-cooled fast reactor | Molten salt reactor | Liquid-metal-cooled reactor | Lead-cooled fast reactor | Sodium-cooled fast reactor | Supercritical water reactor | Very high temperature reactor | Pebble bed reactor | Integral Fast Reactor | Nuclear propulsion | Nuclear thermal rocket | Radioisotope thermoelectric generator
Nuclear medicine	PET | Radiation therapy | Tomotherapy | Proton therapy | Brachytherapy
Nuclear weapons	History of nuclear weapons | Nuclear warfare | Nuclear arms race | Nuclear weapon design | Effects of nuclear explosions | Nuclear testing | Nuclear delivery | Nuclear proliferation | List of states with nuclear weapons | List of nuclear tests

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Nuclear reactor  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Nuclear reactor"

Note: Some restrictions may apply to use of individual images which are separately licensed.