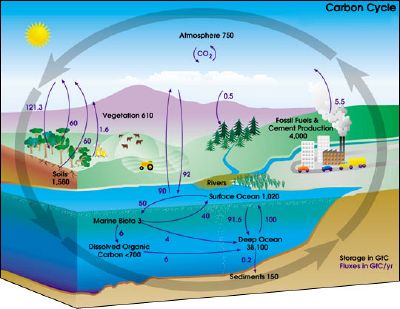
Carbon cycle

Diagram of the carbon cycle. The black numbers indicate how much carbon is stored in various reservoirs, in billions of tons ("GtC" stands for GigaTons of Carbon). The blue numbers indicate how much carbon moves between reservoirs each year.

The carbon cycle is the biogeochemical cycle by which carbon is exchanged between the biosphere, geosphere, hydrosphere, and atmosphere of the earth. (Other planetary bodies may have carbon cycles, but little is known about them.)

The cycle is usually thought of as four main reservoirs of carbon, interconnected by pathways of exchange. These reservoirs are the atmosphere, terrestrial biosphere, oceans, carbonate rocks, and sediments (as organic matter, including fossil fuels). The movement of carbon—the carbon exchanges between reservoirs—occurs because of various chemical, physical, geological, and biological processes. Overall, the carbon cycle reveals the harmonious coordination between different biotic and abiotic elements on Earth.

The global carbon budget is the balance of the exchanges (incomes and losses) of carbon between the carbon reservoirs or between one specific loop (e.g., atmosphere-biosphere) of the carbon cycle. An examination of the carbon budget of a pool or reservoir can provide information about whether that pool or reservoir is functioning as a source or sink for carbon over different time scales.

The carbon cycle is central to understanding issues related to climate change. In resolving the divergent positions with respect to increases of carbon dioxide in the atmosphere and global warming, it is important that scientists maintain integrity in collecting, analyzing, and presenting data in the face of often strong political, commercial, and environmental agendas.

Carbon in the atmosphere

Carbon exists in the Earth's atmosphere primarily as the gas carbon dioxide (CO₂). Although it comprises a very small part of the atmosphere overall (approximately 0.04 percent), it plays an important role in supporting life. Other gases containing carbon in the atmosphere are methane and chlorofluorocarbons (the latter are entirely artificial and are now strictly prohibited under the Montreal Protocol).

Carbon exchange with the atmosphere, biosphere, and oceans

Photosynthesis

Utilizing light from the sun, plants and algae perform photosynthesis to convert carbon dioxide, water, and sunlight into carbohydrates (C₆H₁₂O₆, releasing oxygen in the process. This process removes carbon dioxide from the atmosphere and stores it in plant biomass, which may eventually get buried in sediments after the plant dies.

Respiration

Respiration occurs when the biomass from photosynthetic plants and algae is consumed by animals, fungi, or bacteria, either while the plant is alive, or after it has died. The chemistry of this process is as follows:

O₂ + CH₂O —> Energy + H₂O + CO₂

This is essentially the reverse process of photosynthesis, releasing CO₂ back into the atmosphere. However, more material is photosynthesized than is respired (since a portion of the organic matter is buried in the sediments), thus more oxygen enters the atmosphere than does carbon dioxide as a result of these two processes.

Outgassing

Outgassing of volcanoes and mid-ocean ridges is the largest source of carbon dioxide in the atmosphere, releasing carbon dioxide from deep within the Earth that had been trapped there since the planet's creation. CO₂ is released from subduction zones through metamorphism of carbonate rocks subducting with the ocean crust. Not all of this CO₂ enters the atmosphere. Some of it dissolves in the oceans and some remains in biomass of organisms.

Weathering

Weathering is a mechanism that removes carbon from the atmosphere. When carbon dioxide dissolves in water, it forms carbonic acid. This acid is used to weather rocks, yielding bicarbonate ions in addition to other ions (depending on the mineral content of the rock). The bicarbonate ion enters oceans through fresh water systems, and in the ocean, the bicarbonate ion combines with a calcium ion to form calcium carbonate and a by product of carbon dioxide and water. The calcium carbonate is used by marine organisms to form calcareous shells, and corals use it in their exoskeletons.

Ca⁺⁺ + 2HCO₃- -> CaCO₃ + CO₂ + H₂O

Solubility pump

The solubility pump is a physico-chemical process that transports carbon (as dissolved inorganic carbon) from the ocean's surface to its interior.

The solubility pump is driven by the coincidence of two processes in the ocean:

• The solubility of carbon dioxide is a strong inverse function of seawater temperature (i.e. solubility is greater in cooler water)
• The thermohaline circulation, ocean circulation driven by density differences in salinity and temperature, is driven by the formation of deep water at high latitudes where seawater is usually cooler and more dense

Since deep water (that is, seawater in the ocean's interior) is formed under the same surface conditions that promote carbon dioxide solubility, it contains a higher concentration of dissolved inorganic carbon than one might otherwise expect. Consequently, these two processes act together to pump carbon from the atmosphere into the ocean's interior.

One consequence of this is that when deep water upwells in warmer, equatorial latitudes, it strongly outgasses carbon dioxide to the atmosphere because of the reduced solubility of the gas.

Carbon dioxide solubility

Carbon dioxide, like other gases, is soluble in water. However, unlike many other gases (oxygen for instance), it reacts with water and forms a balance of several ionic and non-ionic species (collectively known as dissolved inorganic carbon, or DIC). These are dissolved free carbon dioxide (CO_{2 (aq)}), carbonic acid (H₂CO₃), bicarbonate (HCO₃^-), and carbonate (CO₃^2-), and they interact with water as follows :

CO_{2 (aq)} + H₂O <—> H₂CO₃ <—> HCO₃^- + H⁺ <—> CO₃^2- + 2 H⁺

The balance of these carbonate species (which ultimately affects the solubility of carbon dioxide), is dependent on factors such as pH. In seawater, this is regulated by the charge balance of a number of positive (e.g. sodium (Na^{+</sup)>, potassium (K+), magnesium (Mg2+), calcium(Ca2+)), and negative (e.g. CO₃2- itself, chlorine (Cl-), (sulfate SO₄2-), bromine (Br-)) ions. Normally, the balance of these species leaves a net positive charge. With respect to the carbonate system, this excess positive charge shifts the balance of carbonate species towards negative ions to compensate. The result of which is a reduced concentration of the free carbon dioxide and carbonic acid species, which in turn leads to an oceanic uptake of carbon dioxide from the atmosphere to restore balance. Thus, the greater the positive charge imbalance, the greater the solubility of carbon dioxide. In carbonate chemistry terms, this imbalance is referred to as alkalinity.}

In terms of measurement, four basic parameters are of key importance: Total inorganic carbon (TIC, T_CO2 or C_T) , Total alkalinity (T_ALK or A_T), pH, and pCO₂. Measuring any two of these parameters allows for the determination of a wide range of pH-dependent species (including the above mentioned species). This balance can be changed by a number of processes. For example, the air-sea flux of CO₂, the dissolution/precipitation of CaCO₃, or biological activity such as photosynthesis/respiration. Each of these has different effects on each of the four basic parameters, and together they exert strong influences on global cycles. It is important to note, the net and local charge of the oceans remains neutral during any chemical process.

Carbon in the biosphere

Carbon is an essential part of life on Earth. It plays an important role in the structure, biochemistry, and nutrition of all living cells. And life plays an important role in the carbon cycle:

• Autotrophs are organisms that produce their own organic compounds using carbon dioxide from the air or water in which they live. To do this they require an external source of energy. Almost all autotrophs use solar radiation to provide this, and their production process is called photosynthesis. A small number of autotrophs exploit chemical energy sources, chemosynthesis. The most important autotrophs for the carbon cycle are trees in forests on land and phytoplankton in the Earth's oceans.
• Carbon is transferred within the biosphere as heterotrophs feed on other organisms or their parts (e.g., fruits). This includes the uptake of dead organic material (detritus) by fungi and bacteria for fermentation or decay.
• Most carbon leaves the biosphere through respiration. When oxygen is present, aerobic respiration occurs, which releases carbon dioxide into the surrounding air or water. Otherwise, anaerobic respiration occurs and releases methane into the surrounding environment, which eventually makes its way into the atmosphere or hydrosphere (e.g., as marsh gas or flatulence).
• Carbon may also leave the biosphere when dead organic matter (such as peat) becomes incorporated in the geosphere. Animal shells of calcium carbonate, in particular, may eventually become limestone through the process of sedimentation.
• Much remains to be learned about the cycling of carbon in the deep ocean. For example, a recent discovery is that larvacean mucus houses (commonly known as "sinkers") are created in such large numbers that they can deliver as much carbon to the deep ocean as has been previously detected by sediment traps (Bennett 2005). Because of their size and composition, these houses are rarely collected in such traps, so most biogeochemical analyses have erroneously ignored them.

Carbon in the oceans

Inorganic carbon, that is, carbon compounds with no carbon-carbon or carbon-hydrogen bonds, is important in its reactions within water. This carbon exchange becomes important in controlling pH in the ocean and can also vary as a source or sink for carbon. Carbon is readily exchanged between the atmosphere and ocean. In regions of oceanic upwelling, carbon is released to the atmosphere. Conversely, regions of down welling transfer carbon (CO₂) from the atmosphere to the ocean. When CO₂ enters the ocean, carbonic acid is formed: CO₂ + H₂O <—> H₂CO₃

This reaction has a forward and reverse rate; that is it achieves a chemical equilibrium.

Another reaction important in controlling oceanic pH levels is the release of hydrogen ions and bicarbonate. This reaction controls large changes in pH: H₂CO₃ <—> H⁺ + HCO₃

Carbon cycle modelling

Models of the carbon cycle can be incorporated into global climate models, so that the interactive response of the oceans and biosphere on future CO₂ levels can be modeled. There are considerable uncertainties in this, both in the physical and biogeochemical submodels (especially the latter). Such models typically show that there is a positive feedback between temperature and CO₂. For example, Zeng et al. (2004) found that, in their model, including a coupled carbon cycle increases atmospheric CO₂ by about 90 ppmv at 2100 (over that predicted in models with non-interactive carbon cycles), leading to an extra 0.6°C of warming (which, in turn, may lead to even greater atmospheric CO₂).

The carbon cycle and climate

Carbon dioxide and methane are two carbon compounds that act as greenhouse gases in Earth's atmosphere, insulating the planet and making it a comfortable place for organisms to survive.

The carbon cycle responds to perturbations through a series of feedbacks so that temperatures never get too hot or too cold, within certain bounds. For example, if CO₂ outgassing from volcanoes and mid-ocean ridges increases as a result of increased tectonic activity, atmospheric temperatures will rise. Rising temperatures and increased amounts of dissolved CO₂ will result in increased rates of weathering of crustal rocks, which will use up the surplus CO₂, decrease atmospheric CO₂ levels, and bring temperatures back down. On the other hand, if global cooling occurred, weathering would slow down and CO₂ would build up in the atmosphere and temperatures would rise again.

The recent debate about anthropogenic (human-induced) climate change has been centered around the release of thousands of tons of carbon dioxide from the burning of fossil fuels and its effect on global climate. Some scientists, using carbon cycle climate models, argue that with the "business as usual" scenario, atmospheric temperatures will rise over the next century (Cox et al. 2000). Other studies suggest that ocean uptake of CO₂ will slow because of increased stratification of the ocean (less deep mixing) (Sarmiento et al. 1998). In addition, increased global temperatures would warm the oceans, decreasing the solubility of CO₂ in ocean water. All of these factors are considered to cause a build up of CO₂ in the atmosphere.

The reason for the concern over anthropogenic climate warming is the possibility that the burning of fossil fuels is releasing carbon into the atmosphere at a rate much faster than the Earth can respond to, to equilibrate and bring conditions back into a steady state, causing climate to possibly react violently at times—not only global temperatures, but increasing storm frequency and intensity. Of course, this scenario remains controversial. In terms of the global warming theory itself, there are other scientists and climatologists that maintain that (1) current fluctuations of global temperatures remain within the normal range of changes over geologic time, or (2) that global temperatures are increasing, albeit slightly, but such changes cannot conclusively be tied to anthropogenic sources or burning of fossil fuels. Other scientists challenge that although the issue remains controversial, a prudent course of action would be to practice the Precautionary Principle that if the consequences of an action are unknown, but are judged to have some potential for major or irreversible negative consequences, then it is better to avoid that action. (Of course, the avoidance of that action might also have potential negative consequences.)

Controversy within science is not uncommon. Clearly, resolution of this important issue will require not only seeking additional hard data, but a willingness of all parties to have an open mind and maintain integrity in accurately presenting and assessing the data collected, and its strengths and weaknesses, versus interpreting everything through the prism of a political, commercial, or environmental agenda.

References

ISBN links support NWE through referral fees

• Cox, P.M., R. A. Betts, C. D. Jones, S. A. Spall, and I. J. Totterdell. 2000. Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature. 408(6809):184-187.
• Janzen, H. H. 2004. Carbon cycling in earth systems—a soil science perspective. Agriculture, ecosystems and environment 104:399–417.
• Houghton, R. A. 2005. The contemporary carbon cycle. Pages 473-513 in W. H. Schlesinger (Ed.), Biogeochemistry. Elsevier Science.
• Robison, B. H., K. R. Reisenbichler, and R. E. Sherlock. 2005. Giant larvacean houses: Rapid carbon transport to the deep seafloor. 2005. Science 308:1609-1611.
• Sarmiento, J. L., A. M. C. Hughes, R. J. Stouffer, and S. Manabe. 1998. Simulated response of the ocean carbon cycle to anthropogenic climate warming. Nature. 393(6682):245-249.
• Zeng, N., H. Qian, E. Munoz, and R. Iacono, R. 2004. How strong is carbon-climate feedback under global warming? Geophysical Research Letters. 31.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Carbon cycle  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Carbon cycle"

Note: Some restrictions may apply to use of individual images which are separately licensed.