Mars

Mars

Mars as seen by the Hubble Space Telescope
Orbital characteristics (Epoch J2000)
Semi-major axis	227,936,637 km (141,632,976 mi) 1.523 662 31 AU
Orbital circumference	1,429,000,000 km (887,900,000 mi) 9.553 AU
Eccentricity	0.093 412 33
Perihelion	206,644,545 km (128,402,967 mi) 1.381 333 46 AU
Aphelion	249,228,730 km (154.863,553 mi) 1.665 991 16 AU
Orbital period	686.9600 d (1.8808 a)
Synodic period	779.96 d (2.135 a)
Avg. Orbital Speed	24.077 km/s (53,859 mi/h)
Max. Orbital Speed	26.499 km/s (59,277 mi/h)
Min. Orbital Speed	21.972 km/s (49,150 mi/h)
Inclination	1.850 61° (5.65° to Sun's equator)
Longitude of the ascending node	49.578 54°
Argument of the perihelion	286.462 30°
Number of natural satellites	2
Physical characteristics
Equatorial diameter	6,804.9 km (4228.4 mi) (0.533 Earths)
Polar diameter	6,754.8 km (4197.2 mi) (0.531 Earths)
Oblateness	0.007 36
Surface area	1.448×108 km² 55,907,000 square miles (144 798 465 square kilometers) (0.284 Earths)
Volume	1.6318×1011 km³ (0.151 Earths)
Mass	6.4185×1023 kg (0.107 Earths)
Mean density	3.934 g/cm³
Equatorial gravity	3.69 m/s2 (0.376g)
Escape velocity	5.027 km/s (11,245 mi/h)
Rotation period	1.025 957 d (24.622 962 h)
Rotation velocity	868.22 km/h (539.49 mi/h) (at the equator)
Axial tilt	25.19°
Right ascension of North pole	317.681 43° (21 h 10 min 44 s)
Declination	52.886 50°
Albedo	0.15
Surface temp. - min - mean - max	−140 °C (133 K) −63 °C (210 K) 20 °C (293 K)
Adjective	Martian
Atmospheric characteristics
Atmospheric pressure	0.7–0.9 kPa
Carbon dioxide	95.32%
Nitrogen	2.7%
Argon	1.6%
Oxygen	0.13%
Carbon monoxide	0.07%
Water vapor	0.03%
Nitric oxide	0.01%
Neon	2.5 ppm
Krypton	300 ppb
Xenon	80 ppb
Ozone	30 ppb
Methane	10.5 ppb

Mars is the fourth planet from the Sun in our solar system and is named after the Roman god of war. It is also known as the "Red Planet," due to its reddish appearance when seen from the Earth.

Like the Earth, Mars has a rocky surface and polar ice caps. Its rotational period and seasonal cycles are similar to those of the Earth. Of all the planets in the Solar System, it has the highest mountain, Olympus Mons, and the largest canyon, Valles Marineris. The availability of Mars samples in the form of Martian meteorites gives "ground-truth" data to researchers, just as in the case of studying meteorites from the Moon. In addition, Mars has two moons, Phobos and Deimos, both of which are small and oddly shaped.

Until the first flyby of Mars by Mariner 4 in 1965, many thought that the planet might have ample liquid water. This belief was based on early observations of Mars, showing periodic variations in light and dark patches, particularly in the polar latitudes, and long dark striations that suggested the presence of irrigation channels of liquid water. Subsequent analyses indicated that the striations were optical illusions.

Nonetheless, of all the planets in the solar system other than Earth, Mars is thought to be the most likely to harbor liquid water, and perhaps some life forms. Consequently, popular attention has been drawn to Mars, and probes to this planet continue to be equipped with instruments to attempt to discover microscopic life. In addition, some think that we may be able to make Mars habitable in the future—a concept known as "terraforming."

As of early 2009, Mars is host to three orbiting spacecraft: Mars Odyssey, Mars Express, and Mars Reconnaissance Orbiter. It is also home to two Mars Exploration Rovers, Spirit and Opportunity.

Viewing Mars

When seen from Earth with the naked eye, Mars usually appears to have a distinct yellow, orange, or reddish color. Its brightness varies over the course of its orbit, more so than the brightness of any other planet. The apparent magnitude of its brightness can be as high as -2.9, a value surpassed only by Venus, the Moon, and the Sun. For much of the year, Jupiter may appear brighter to the naked eye than Mars.

During its orbit, the farthest point of Mars from Earth is more than seven times its closest point. When least favorably positioned, it can be lost in the Sun's glare for months at a time. It is most favorably positioned twice every 32 years, alternately at 15- and 17-year intervals, and always between late July and late September. During those times, a wealth of surface detail can be observed through a telescope. Especially noticeable, even at low magnification, are the polar ice caps.

Approximately every 780 days, opposition occurs, which is about when Mars is nearest to Earth. Given the eccentricities of the orbits, the times of opposition and minimum distance can differ by up to 8.5 days. The minimum distance varies between about 55 and 100 million kilometers, due to the planets' elliptical orbits.

On August 27, 2003, at 9:51:13 UT, Mars made its closest approach to Earth in nearly 60,000 years: 55,758,006 kilometers (approximately 35 million miles). This occurred when Mars was one day from opposition and about three days from its perihelion, making Mars particularly easy to see from Earth. The last time it came so close is estimated to have been on September 12, 57,617 B.C.E., and the next time will be in 2287. However, this record approach was only very slightly closer than other recent close approaches. For instance, the minimum distance on August 22, 1924 was 0.37284 astronomical units (AU) (compared to 0.37271 AU on August 27, 2003).

The orbital changes of Earth and Mars are making the approaches nearer: the 2003 record will be bettered 22 times by the year 4000.

Historical observations of Mars

Map of Mars by Giovanni Schiaparelli

The history of observations of Mars is marked by the oppositions of Mars, when the planet is closest to Earth and hence is most easily visible, which occur every couple of years. Even more notable are the perihelic oppositions of Mars, which occur approximately every 16 years and are distinguished because Mars is close to perihelion, making it even closer to Earth.

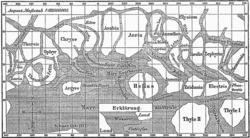
By the nineteenth century, the resolution of telescopes reached a level sufficient for surface features to be identified. A perihelic opposition of Mars occurred on September 5, 1877. In that year, Italian astronomer Giovanni Schiaparelli used a 22-centimeter telescope in Milan to help produce the first detailed map of Mars. These maps notably contained features he called canali, which were later shown to be an optical illusion. These canali were supposedly long straight lines on the surface of Mars to which he gave names of famous rivers on Earth. His term was popularly mistranslated as “canals.”

Influenced by the observations, the orientalist Percival Lowell founded an observatory that had 12- and 18-inch telescopes. The observatory was used for the exploration of Mars during the last good opportunity in 1894 and the following less favorable oppositions. He published several books on Mars and life on Mars that greatly influenced the public mind. The canali were also observed by other astronomers, such as Perrotin and Thollon in Nice, using one of the largest telescopes of that time.

The seasonal changes (consisting of the diminishing of the polar caps and the dark areas formed during the Martian summer) in combination with the canals led to speculation about life on Mars, and it was a long-held belief that Mars contained vast seas and vegetation. The telescope never reached the resolution required to give proof to any speculations. However, as bigger telescopes were used, fewer long, straight canali were observed. During an observation in 1909 by Flammarion with a 33-inch telescope, irregular patterns were observed, but no canali were seen.

Even in the 1960s, articles were published on Martian biology, putting aside explanations other than life for the seasonal changes on Mars. Detailed scenarios for the metabolism and chemical cycles for a functional ecosystem were published.

It was not until spacecraft visited the planet during NASA's Mariner missions in the 1960s that these myths were dispelled. The results of the Viking life detection experiments started an intermission in which the hypothesis of a dead Mars, hostile to life, was generally accepted.

Some maps of Mars were made using the data from these missions, but it wasn't until the Mars Global Surveyor mission, launched in 1996 (and operational as of 2006), that complete, extremely detailed maps were obtained.

Mars in early human culture

In Roman mythology, Mars was the god of war and patron of warriors. The symbol for Mars is a circle with a small arrow pointing out from behind it, which is a stylized representation of a shield and spear used by the Roman god. This symbol is also used in biology to denote the male sex.

In Babylonian astronomy, the planet was named after Nergal, their deity of fire, war, and destruction, most likely due to the planet's reddish appearance. When the Greeks equated Nergal with their god of war, Ares, they named the planet Areos aster, or "star of Ares." Then, following the identification of Ares and Mars, it was translated into Latin as stella Martis, or "star of Mars," or simply Mars. The Greeks also called the planet Pyroeis, meaning "fiery."

In Hindu mythology, Mars is known as Mangala. It is also called Angaraka in Sanskrit. He is the god of war and is celibate. He is the owner of the Aries and Scorpio signs, and a teacher of the occult sciences. The planet was known by the ancient Egyptians as "Horus the Red." The Hebrews named it Ma'adim, or "the one who blushes." This is where one of the largest canyons on Mars, the Ma'adim Vallis, gets its name. It is known as al-Mirrikh in both Arabic and Persian, and Merih in Turkish. The etymology of al-Mirrikh is unknown. Ancient Persians named it Bahram, the Zoroastrian god of faith. Ancient Turks called it Sakit. The Chinese, Japanese, Korean, and Vietnamese cultures refer to the planet as fire star, a naming based on the ancient Chinese philosophical group of Five Elements.

Physical characteristics

Size comparison of terrestrial planets (left to right): Mercury, Venus, Earth, and Mars

The red/orange appearance of Mars' surface is caused by iron(III) oxide (rust). Mars has half the radius of the Earth and only one-tenth the mass. It is less dense, and its surface area is only slightly less than the total area of Earth's dry land. While Mars is larger and more massive than Mercury, Mercury has higher density and therefore has slightly stronger gravity at its surface.

Geology

The surface of Mars is thought to be primarily composed of basalt, based upon the Martian meteorite collection and orbital observations. There is some evidence that a portion of the Martian surface might be more silica-rich than typical basalt, perhaps similar to andesitic stones on Earth, though these observations may also be explained by silica glass. Much of the surface is deeply covered by iron(III) oxide dust.

Photo of microscopic rock forms indicating past signs of water, taken by the rover Opportunity.

There is conclusive evidence that liquid water existed at one time on the surface of Mars. Key discoveries leading to this conclusion include the detection of various minerals, such as hematite and goethite, which usually form only in the presence of water.

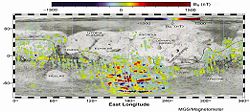
Although Mars has no intrinsic magnetic field, observations have revealed that parts of the planet's crust have been magnetized. This magnetization has been compared to alternating bands found on the ocean floors of Earth. One theory, published in 1999 and reexamined in October 2005 with the help of the Mars Global Surveyor, is that these bands are evidence of the past operation of plate tectonics on Mars. It is also possible to explain this "paleomagnetism" (record of the past magnetic field in certain magnetized minerals) based on shifting of the magnetic poles.

Current models of the planet's interior infer a core region approximately 1,480 kilometers (km) in radius, consisting primarily of iron with about 15-17 percent sulfur. This iron sulfide core is partially fluid, with twice the concentration of light elements that exist in the Earth's core. The core is surrounded by a silicate mantle that formed many of the tectonic and volcanic features on the planet, but now appears to be inactive. The average thickness of the planet's crust is about 50 km, and it is no thicker than 125 km.

The geological history of Mars is split into three broad epochs:

• Noachian epoch (named after Noachis Terra): From the formation of Mars to between 3,800 and 3,500 million years ago. Noachian age surfaces are scarred by many large impact craters. The Tharsis bulge is thought to have formed during this period, with extensive flooding by liquid water late in the epoch.
• Hesperian epoch (named after Hesperia Planum): From 3,500 million years ago to 1,800 million years ago. The Hesperian epoch is marked by the formation of extensive lava plains.
• Amazonian epoch (named after Amazonis Planitia): From 1,800 million years ago to the present. Amazonian regions have few meteorite impact craters but are otherwise quite varied. Olympus Mons formed during this period, along with lava flows elsewhere on Mars.

An alternative series of classifications has also been put forward, based on data from an instrument (the OMEGA Visible and Infrared Mineralogical Mapping Spectrometer) on board the Mars Express orbiter.

Geography of Mars (Areography)

Topographic map of Mars. Notable features include the Tharsis volcanoes in the west (including Olympus Mons), Valles Marineris to the east of Tharsis, and Hellas Basin in the southern hemisphere.

Although better remembered for mapping the Moon starting in 1830, Johann Heinrich Mädler and Wilhelm Beer were the first "aerographers." They started off by establishing once and for all that most of Mars' surface features were permanent, and pinned down Mars' rotation period. In 1840 Mädler combined ten years of observations and drew the first ever map of Mars. Rather than giving names to the various markings they mapped, Beer and Mädler simply designated them with letters; Meridian Bay (Sinus Meridiani) was thus feature "a."

Today, features on Mars are named from a number of sources. Large albedo (visible reflectivity) features retain many of the older names, but are often updated to reflect new knowledge of the nature of the features. For example, Nix Olympica (the snows of Olympus) has become Olympus Mons (Mount Olympus).

Mars' equator is defined by its rotation, but the location of its Prime Meridian was specified (as was Earth's) by choice of an arbitrary point. Mädler and Beer selected a line in 1830 for their first maps of Mars. After the spacecraft Mariner 9 provided extensive imagery of Mars in 1972, a small crater (later called Airy-0), located in the Sinus Meridiani ("Middle Bay" or "Meridian Bay"), was chosen for the definition of 0.0° longitude to coincide with the originally selected line.

Since Mars has no oceans and hence no 'sea level,' a zero-elevation surface or mean gravity surface must be selected. The zero altitude is defined by the height at which there is 610.5 pascals (Pa) (6.105 mbar) of atmospheric pressure (approximately 0.6 percent that of Earth's). This pressure corresponds to the triple point of water.

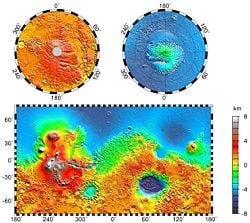
The dichotomy of Martian topography is striking: northern plains flattened by lava flows contrast with the southern highlands, pitted and cratered by ancient impacts. The surface of Mars as seen from Earth is thus divided into two kinds of areas, with differing albedo. The paler plains covered with dust and sand rich in reddish iron oxides were once thought of as Martian 'continents' and given names like Arabia Terra (land of Arabia) or Amazonis Planitia (Amazonian plain). The dark features were thought to be seas, hence their names Mare Erythraeum, Mare Sirenum, and Aurorae Sinus. The largest dark feature seen from Earth is Syrtis Major.

The shield volcano, Olympus Mons (Mount Olympus), with a height of 26,000 meters, is the highest known mountain in the solar system. It is an extinct volcano in the vast upland region Tharsis, which contains several other large volcanoes. It is over three times the height of Mt. Everest, which stands at 8,848 meters.

Mars is also scarred by a number of impact craters. The largest of these is the Hellas impact basin, covered with light red sand. Despite being closer to the asteroid belt, there are far fewer craters on Mars compared with the Moon, because Mars' atmosphere provides protection against small meteors. Some craters have a morphology that suggests that the ground was wet when the meteor impacted.

The large canyon Valles Marineris (Latin for Mariner Valleys, also known as Agathadaemon in the old canal maps) has a length of 4,000 kilometers and a depth of up to 7 km. The length of Valles Marineris is equivalent to the length of Europe and extends across one-fifth the circumference of Mars. By comparison, the Grand Canyon on Earth is only 446 km long and nearly 2 km deep. Valles Marineris was formed due to the swelling of the Tharis area, which caused the crust in the area of Valles Marineris to collapse. Another large canyon is Ma'adim Vallis (Ma'adim is Hebrew for Mars). It is 700 km long and again much bigger than the Grand Canyon, with a width of 20 km and a depth of 2 km in some places. It is possible that Ma'adim Vallis was flooded with liquid water in the past.

Atmosphere

Mars in 2001, with polar ice caps visible

The atmosphere of Mars is relatively thin; the atmospheric pressure on the surface varies from around 30 Pa (0.03 kPa) on Olympus Mons to over 1,155 Pa (1.155 kPa) in the depths of Hellas Planitia, with a mean surface-level pressure of 600 Pa (0.6 kPa), compared to Earth's 101.3 kPa. The equivalent pressure of Mars' atmosphere can be found at a height of 35 km above the Earth's surface. The scale height of the atmosphere is about 11 km, higher than Earth's 6 km.

The atmosphere on Mars consists of 95 percent carbon dioxide, 3 percent nitrogen, 1.6 percent argon, and traces of oxygen and water. The atmosphere is quite dusty, giving the Martian sky a tawny color when seen from the surface; the particulates responsible are about 1.5 µm across.

Several researchers claim to have detected methane in the Martian atmosphere, at a concentration of about 10 parts per billion (ppb) by volume. Methane is an unstable gas that is broken down by ultraviolet radiation, typically lasting in the atmosphere for about 340 years, and its possible presence on Mars could indicate that there is (or has been within the last few hundred years) a source of the gas on the planet. Possible sources include volcanic activity, comet impacts, and microorganisms such as methanogens. It was recently shown that methane could also be produced by a nonbiological process involving water, carbon dioxide, and the mineral olivine, which is believed to be common on Mars.

In the winter months when the poles are in continuous darkness, the surface gets so cold that as much as 25–30 percent of the entire atmosphere condenses out into thick slabs of CO₂ ice (dry ice).

When the poles are again exposed to sunlight, the CO₂ ice sublimes (is converted directly to gas), creating enormous winds that sweep off the poles as fast as 400 kilometers per hour (km/h) (250 miles per hour (mph)). These seasonal actions transport large amounts of dust and water vapor, giving rise to Earth-like frost and large, cirrus clouds. Clouds of water-ice were photographed by the Opportunity rover in 2004.

Strength of Mars' magnetic field (red and blue indicate stronger than average areas)

Magnetosphere

Evidence indicates that in Mars' distant past, it may have had a strong enough magnetosphere to deflect the solar wind (from the Sun). However, about four billion years ago, Mars' planetary dynamo ceased, leaving only remnants of the planetary magnetic field to be frozen into magnetically susceptible minerals. Over time, most of this material was reprocessed through various geological events leaving only sections of the ancient southern highlands with remnant magnetic fields. Because of this, the solar wind interacts directly with the Martian ionosphere and thus the Martian atmosphere has been slowly stripped off into space, although the exact amount lost remains uncertain. Both Mars Global Surveyor and Mars Express have detected ionized atmospheric particles trailing off into space behind Mars.

Mars from Hubble Space Telescope, October 28, 2005, with duststorm visible

Climate

Of all the planets, Mars' seasons are the most Earth-like, due to the similar tilts of the two planets' rotational axes. However, the lengths of the Martian seasons are about twice those of Earth's, as Mars' greater distance from the sun leads to the Martian year being approximately two Earth years in length. Martian surface temperatures vary from approximately -140 °C to 0 °C Recent evidence has suggested that Mars is subject to short-term regional climate changes.

If Mars had an Earth-like orbit, its seasons would be similar to Earth's because its axial tilt is similar to Earth's. However, the comparatively large eccentricity of the Martian orbit has a significant effect. Mars is near perihelion (closest point to the Sun) when it is summer in the southern hemisphere and winter in the north, and near aphelion (farthest point from the Sun) when it is winter in the southern hemisphere and summer in the north. As a result, the seasons in the southern hemisphere are more extreme and the seasons in the northern are milder than would otherwise be the case.

Mars' northern ice cap

Mars also has the largest dust storms in the solar system. These can vary in size from a storm covering a small area to gigantic storms that cover the entire planet. They tend to occur when Mars is closest to the Sun, which increases the global temperature.

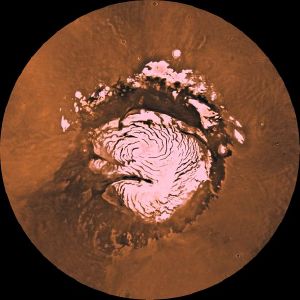
Mars possesses polar caps at both poles, which mainly consist of water ice. Frozen carbon dioxide (dry ice) accumulates as a thin layer (about one meter thick) on the north cap in the northern winter only, while the south cap has a permanent dry ice cover, about eight meters thick. The northern polar cap has a diameter of approximately 1,000 kilometers during the northern Mars summer, and contains about 1.6 million kilometers³ of ice, which, if spread evenly on the cap, would be 2 kilometers thick The southern polar cap has a diameter of 350 kilometers, and a thickness of 3 kilometers. Both polar caps show spiral cuts, which remain unexplained. Both polar caps shrink and re-grow following temperature fluctuations of the Martian seasons.

Orbit and rotation

Mars has a relatively pronounced orbital eccentricity of about 9 percent. Of the other planets in the solar system, only Mercury shows greater eccentricity. Mars' average distance from the Sun is roughly 230 million kilometers (1.5 AU) and its orbital period is 687 (Earth) days. The solar day (or sol) on Mars is only slightly longer than an Earth day: 24 hours, 39 minutes, and 35.244 seconds.

Mars' axial tilt is 25.19 degrees, which is similar to the axial tilt of the Earth. As a result, Mars has seasons like the Earth, though Mars' are about twice as long given its longer year.

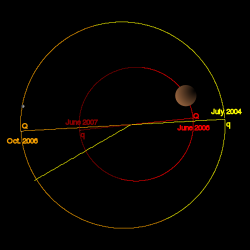
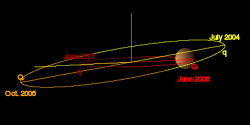
The image to the right shows a comparison between Mars and Ceres, a dwarf planet in the asteroid belt, as seen from the ecliptic pole (upper image) and from the ascending node (lower image). The segments of orbits below the ecliptic are plotted in darker colors. The perihelia (q) and aphelia (Q) are labeled with the date of the nearest passage.

Moons

Phobos (top) and Deimos (bottom) are the two moons orbiting Mars

Mars has two tiny natural satellites, Phobos and Deimos, that orbit very close to the planet. These moons may be captured asteroids, similar to 5261 Eureka, which has been labeled a "Trojan asteroid" of Mars. Phobos and Deimos are believed to have generated a dust ring around Mars, and thus have been highly space-weathered by repeated impacts of their own dust particles.

Both satellites were discovered in 1877 by Asaph Hall and are named after the Greek mythological characters Phobos (panic/fear) and Deimos (terror/dread), who accompanied their father Ares, the god of war, into battle. Ares was known as Mars to the Romans.

From the Martian surface, the motions of Phobos and Deimos appear very different from that of our own Moon. Phobos rises in the west, sets in the east, and rises again in just 11 hours. Deimos, being only just outside synchronous orbit, rises as expected in the east but very slowly. Despite its 30 hour orbit, it takes 2.7 days to set in the west as it slowly falls behind the rotation of Mars, and it takes as long again to rise.

Because Phobos' orbit is below synchronous altitude, the tidal forces are lowering its orbit. It has been predicted that in about 50 million years, it will either crash into Mars' surface or break up into a ring structure around the planet.

Famous literary author Jonathan Swift made reference to these moons of Mars approximately 150 years before their actual discovery by Asaph Hall, detailing reasonably accurate descriptions of their orbits in the nineteenth chapter of his novel Gulliver's Travels.

Life

Some evidence suggests that the planet was once significantly more habitable than it is today, but it is still an open question whether living organisms ever existed there. The Viking probes of the mid-1970s carried experiments designed to detect microorganisms in Martian soil at their respective landing sites. They gave some apparently positive results that were later disputed by many scientists, resulting in a continuing fight.

At the Johnson space center lab, organic compounds have been found in the meteorite ALH84001, which is supposed to have come from Mars. They concluded that these were deposited by primitive life forms extant on Mars before the meteorite was blasted into space by a meteor strike and sent on a 15 million-year-voyage to Earth. Small quantities of methane, and formaldehyde are both claimed to be hints for life, as these particles would quickly break down in the Martian atmosphere. It is possible that these compounds may be replenished by volcanic or geological means, such as serpentinization.

In general, Mars shows some promise in terms of habitablity but also several handicaps. It is half of an astronomical unit beyond the Sun's habitable zone and water is thus frozen on its surface, although liquid water flows in the past suggest the planet's potential. Its lack of a magnetosphere and extremely thin atmosphere are a greater challenge: the planet has little heat transfer across its surface, poor insulation against bombardment and the solar wind, and insufficient atmospheric pressure to keep water in liquid form—instead, it sublimates to a gaseous state. Mars is also nearly, or perhaps totally, geologically dead. The end of volcanic activity has stopped the recycling of chemicals and minerals between the surface and interior of the planet.

Exploration

Dozens of spacecraft—including orbiters, landers, and rovers—have been sent to Mars by the former Soviet Union, the United States, Europe, and Japan to study the planet's surface, climate, and geology.

Roughly two-thirds of all spacecraft destined for Mars have failed in one manner or other before completing or even beginning their missions. Part of this high failure rate can be ascribed to technical problems, but enough have either failed or lost communications for no apparent reason that some researchers half-jokingly speak of an Earth-Mars "Bermuda Triangle," or a Mars Curse, or even a reference made to a "Great Galactic Ghoul" that feeds on Martian spacecraft.

Past missions

The first successful fly-by mission to Mars was NASA's Mariner 4, launched in 1964. The first successful objects to land on the surface were two Soviet probes, Mars 2 and Mars 3, from the Mars probe program launched in 1971, but both lost contact within seconds of landing. Then came the 1975 NASA launches of the Viking program, which consisted of two orbiters, each having a lander. Both landers successfully touched down in 1976 and remained operational for 6 and 3 years, for Viking 1 and Viking 2 respectively. The Viking landers relayed the first color pictures of Mars. They also mapped the surface of Mars so well that the images are still sometimes used. The Soviet probes Phobos 1 and 2 were also sent to Mars in 1988 to study Mars and its two moons. Unfortunately, Phobos 1 lost contact on the way to Mars, and Phobos 2, while successfully photographing Mars and Phobos, failed just before it was set to release two landers onto Phobos' surface.

Recent missions

Following the 1992 failure of Mars Observer orbiter, NASA launched the Mars Global Surveyor in 1996. This mission was a complete success, having finished its primary mapping mission in early 2001. Only a month after the launch of the Surveyor, NASA launched the Mars Pathfinder, carrying a robotic exploration vehicle, which landed in the Ares Vallis on Mars. This mission was another big success, and received much publicity, partially due to the many spectacular images that were sent back to Earth.

Artist's concept of the 2001 Mars Odyssey

In 2001 NASA launched the successful Mars Odyssey orbiter. Odyssey's Gamma Ray Spectrometer detected significant amounts of elemental hydrogen in the upper meter or so of Mars' regolith. This hydrogen is thought to be contained in large deposits of water ice.

In 2003 the European Space Agency (ESA) launched the Mars Express craft consisting of the Mars Express Orbiter and the lander Beagle 2. Beagle 2 apparently failed during descent and was declared lost in early February 2004. In early 2004, the Planetary Fourier Spectrometer team announced it had detected methane in the Martian atmosphere. ESA announced in June 2006 the discovery of aurorae on Mars.

Also in 2003, NASA launched the twin Mars Exploration Rovers named Spirit (MER-A) and Opportunity (MER-B). Both missions landed successfully in January 2004 and have met or exceeded all their targets. Among the most significant science returns has been the conclusive evidence that liquid water existed at some time in the past at both landing sites. Martian dust devils and windstorms have occasionally cleaned both rovers' solar panels, and thus increased their lifespan.

On August 12, 2005, the NASA Mars Reconnaissance Orbiter probe was launched toward the planet, to conduct a two-year science survey. The purpose of the mission is to map the Martian terrain and find suitable landing sites for the upcoming lander missions. It arrived in orbit on March 10, 2006.

Astronomical observations from Mars

Earth and Moon from Mars, imaged by Mars Global Surveyor; South America is visible

Given the various orbiters, landers, and rovers, it is now possible to study astronomy from the Martian skies. In particular, the Earth and the Moon would be easily visible to the naked eye from Mars. Also, one could observe the two moons of Mars. The moon Phobos appears about one-third the angular diameter that the full Moon appears from Earth, and when it is full it is bright enough to cast shadows. On the other hand, Deimos appears more or less star-like, and appears only slightly brighter than Venus does from Earth.

There are also various phenomena well-known on Earth that have now been observed on Mars, including meteors and auroras. The first meteor photographed on Mars was on March 7, 2004, by the rover Spirit. Auroras occur on Mars, but they do not occur at the poles as on Earth, because Mars has no planet-wide magnetic field. Rather, they occur near magnetic anomalies in Mars' crust, which are remnants from earlier days when Mars did have a magnetic field. They would probably be invisible to the naked eye, being largely ultraviolet phenomena.

A transit of the Earth as seen from Mars will occur on November 10, 2084. At that time, the Sun, Earth and Mars will be exactly collinear. There are also transits of Mercury and transits of Venus, and the moon Deimos is of sufficiently small angular diameter that its partial "eclipses" of the Sun are best considered transits.

Photograph of a Martian sunset taken by Spirit at Gusev crater, May 19, 2005

The only occultation of Mars by Venus observed was that of October 3, 1590, seen by M. Möstlin at Heidelberg.

Future plans

Manned Mars exploration by the United States has been explicitly identified as a long-term goal in the Vision for Space Exploration announced in 2004 by President George W. Bush.

The European Space Agency hopes to land the first humans on Mars between 2030 and 2035. This will be preceded by successively larger probes, starting with the launch of the ExoMars probe in 2013, followed by the 'Mars Sample Return Mission.' Likewise, astronauts will be sent to the Moon between 2020 and 2025 in preparation for this mission.

Mars in fiction

The depiction of Mars in fiction has been stimulated by its dramatic red color and by early scientific speculations that its surface conditions might be capable of supporting life. Until the arrival of planetary probes, the traditional view of Mars derived from the astronomers such as Giovanni Schiaparelli and Percival Lowell, whose observation of supposedly linear features on the planet created the myth of canals on Mars. For many years, the standard notion of the planet was a drying, cooling, dying world with ancient civilizations constructing irrigation works.

Thus originated a large number of science fiction scenarios, the best known of which is H. G. Wells' The War of the Worlds, in which Martians seek to escape their dying planet by invading Earth. Of considerable note is the release of a radio broadcast of The War of the Worlds on October 30, 1938. It was broadcast as a news release, and many people mistook it for the truth. Also influential was Ray Bradbury's The Martian Chronicles, in which human explorers find a dying Martian civilization, as well as Burroughs' Barsoom series and a number of Robert A. Heinlein stories prior to the mid-sixties.

After the Mariner and Viking spacecraft had returned images that showed Mars to be an apparently lifeless and canal-less world, these ideas about Mars had to be abandoned. Since then, a vogue for realist depictions of human colonies on Mars developed, the best known of which may be Kim Stanley Robinson's Mars trilogy. Nonetheless, pseudo-scientific speculations about the Face on Mars and other enigmatic landmarks spotted by space probes have meant that ancient civilizations continue to be a popular theme in science fiction, especially in film.

Another popular theme, particularly among American writers, is the Martian colony that fights for independence from Earth. This is a major plot element in the novels of Greg Bear and Kim Stanley Robinson, as well as the movie Total Recall (based on a short story by Philip K. Dick) and the television series Babylon 5. Many video games also use this element, such as Red Faction and the Zone of the Enders series. Mars (and its moons) were also the setting for the popular Doom video-game franchise and the later Martian Gothic.

See also

• Astrobiology
• Earth
• Planet
• Solar System
• Sun

References

ISBN links support NWE through referral fees

• Sheehan, William. The Planet Mars: A History of Observation and Discovery. Tuscon, AZ: The University of Arizona Press, 1996. Retrieved January 23, 2017.
• Nine Planets Mars page. Retrieved January 23, 2017.
• Space.com: Mars Facts: Life, Water and Robots on the Red Planet Retrieved January 23, 2017.
• Squyres, Steve. Roving Mars: Spirit, Opportunity, and the Exploration of the Red Planet. New York: Hyperion, 2005. ISBN 1401301495

External links

All links retrieved November 6, 2022.

• NASA's Mars fact sheet
• 3D maps of Mars - WorldWind Central
• Google Mars - Interactive image of Mars
• Freie Universität Berlin: HRSC (camera) experiment at Mars Express - Press releases and high resolution images
• Technical Notes about Time on Mars
• On Mars: Exploration of the Red Planet 1958-1978 from the NASA History Office.
• A Trip Into Space - Photos and descriptions of Mars
• Ralph Aeschliman's Online Atlas of Mars
• Planets - Mars A kid's guide to Mars.
• BBC: Wheels turn on Mars rover project
• Geody Mars World's search engine that supports NASA World Wind, Celestia, and other applications.
• NASA Mars Exploration Rover Home Page
• Be on Mars - Anaglyphs from the Mars Rovers (3D)

Water

• Ice lake found on the Red Planet - BBC
• Ice reservoirs found on Mars - BBC
• Long history of water and Mars - BBC
• Mars Rover Scientists Wring Water Story from Rocks - This image taken by Mars Rover Opportunity shows microscopic rock forms indicating past signs of water. Courtesy: NASA
• Mars pictures reveal frozen sea BBC

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Mars  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Mars"

Note: Some restrictions may apply to use of individual images which are separately licensed.