Acceleration

An F/A-18 Hornet just before breaking the sound barrier. The condensation cloud surrounding the aircraft is thought to result from a sudden drop in air pressure (called the Prandtl-Glauert singularity).

In physics, acceleration is defined as the rate of change of velocity—that is, the change of velocity with time. An object is said to undergo acceleration if it is changing its speed or direction or both. A device used for measuring acceleration is called an accelerometer.

Explanation

An object traveling in a straight line undergoes acceleration when its speed changes. An object traveling in a uniform circular motion at a constant speed is also said to undergo acceleration because its direction is changing.

The term "acceleration" generally refers to the change in instantaneous velocity. Given that velocity is a vector quantity, acceleration is also a vector quantity. This means that it is defined by properties of magnitude (size or measurability) and direction.

In the strict mathematical sense, acceleration can have a positive or negative value. A negative value for acceleration is commonly called deceleration.

The dimension for acceleration is length/time². In SI units, acceleration is measured in meters per second squared (m•s^-²).

Acceleration is the change of velocity with time, whether the change occurs in terms of speed or direction or both. On a velocity-time graph, the acceleration at any point is given by the slope of the tangent to the curve at that point.

Since:

${\vec {F}}={\mathrm {d} {\vec {p}} \over \mathrm {d} t}$

Then, for the definition of instantaneous acceleration;

$A=\lim _{dt\rightarrow 0}{\frac {dv}{dt}}={\frac {dv}{dt}}={\frac {d}{dt}}({\frac {dx}{dt}})={\frac {d^{2}x}{dt^{2}}}$

also $\mathbf {v} =\int _{0}^{n}({\mathrm {d} \mathbf {v} \over \mathrm {d} t})\,dt$ OR $\mathbf {v} =\int _{0}^{n}\mathbf {a} \,dt$, i.e. Velocity can be thought of as the integral of acceleration with respect to the time. (Note, this can be a definite or indefinite integration).

$\mathbf {a}$ is the acceleration vector (as acceleration is a vector, it must be described with both a direction and a has a magnitude)

v is the velocity function

x is the position function (also known as displacement or change in position)

t is time

d is Leibniz's notation for differentiation

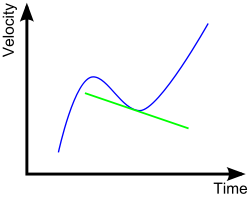
When velocity is plotted against time on a velocity vs. time graph, the acceleration is given by the slope, or the derivative of the graph.

If used with SI standard units (metres per second for velocity; seconds for time) this equation gives a the units of m/(s•s), or m/s² (read as "metres per second per second," or "metres per second squared").

An average acceleration, or acceleration over time, ā can be defined as:

$\mathbf {\bar {a}} ={\mathbf {v} -\mathbf {u} \over t}$

where

u is the initial velocity (m/s)

v is the final velocity (m/s)

t is the time interval (s) elapsed between the two velocity measurements (also written as "Δt")

Transverse acceleration (perpendicular to velocity), as with any acceleration which is not parallel to the direction of motion, causes change in direction. If it is constant in magnitude and changing in direction with the velocity, we get a circular motion. For this centripetal acceleration we have:

$\mathbf {a} =-{\frac {v^{2}}{r}}{\frac {\mathbf {r} }{r}}=-\omega ^{2}\mathbf {r}$

One common unit of acceleration is g, one g (more specifically, g_n or g ₀) being the standard uniform acceleration of free fall or 9.80665 m/s², caused by the gravitational field of Earth at sea level at about 45.5° latitude.

Jerk is the rate of change of an object's acceleration over time.

In classical mechanics, acceleration $a\$ is related to force $F\$ and mass $m\$ (assumed to be constant) by way of Newton's second law:

$\mathbf {F} =m\cdot \mathbf {a}$

As a result of its invariance under the Galilean transformations, acceleration is an absolute quantity in classical mechanics.

Relation to relativity

After defining his theory of special relativity, Albert Einstein realized that forces felt by objects undergoing constant proper acceleration are indistinguishable from those in a gravitational field, and thus defined general relativity that also explained how gravity's effects could be limited by the speed of light.

If you accelerate away from your friend, you could say (given your frame of reference) that it is your friend who is accelerating away from you, although only you feel any force. This is also the basis for the popular Twin paradox, which asks why only one twin ages when moving away from his sibling at near light-speed and then returning, since the aging twin can say that it is the other twin that was moving.

General relativity solved the "why does only one object feel accelerated?" problem which had plagued philosophers and scientists since Newton's time (and caused Newton to endorse absolute space). In special relativity, only inertial frames of reference (non-accelerated frames) can be used and are equivalent; general relativity considers all frames, even accelerated ones, to be equivalent. With changing velocity, accelerated objects exist in warped space (as do those that reside in a gravitational field). Therefore, frames of reference must include a description of their local spacetime curvature to qualify as complete.

Accelerometer

An accelerometer inherently measures its own motion (locomotion). It thus differs from a device based on remote sensing. Accelerometers can be used to measure vibration on cars, machines, buildings, process control systems and safety installations. They can also be used to measure seismic activity, inclination, machine vibration, dynamic distance and speed with or without the influence of gravity.

One application for accelerometers is to measure gravity, wherein an accelerometer is specifically configured for use in gravimetry. Such a device is called a gravimeter. Accelerometers are being incorporated into more and more personal electronic devices such as mobile phones, media players, and handheld gaming devices. In particular, more and more smartphones are incorporating accelerometers for step counters, user interface control, and switching between portrait and landscape modes.

Accelerometers are used along with gyroscopes in inertial guidance systems, as well as in many other scientific and engineering systems. One of the most common uses for micro electro-mechanical system (MEMS) accelerometers is in airbag deployment systems for modern automobiles. In this case, the accelerometers are used to detect the rapid negative acceleration of the vehicle to determine when a collision has occurred and the severity of the collision.

Accelerometers are perhaps the simplest MEMS device possible, sometimes consisting of little more than a suspended cantilever beam or proof mass (also known as seismic mass) with some type of deflection sensing and circuitry. MEMS Accelerometers are available in a wide variety of ranges up to thousands of g_n's. Single axis, dual axis, and three axis models are available.

The widespread use of accelerometers in the automotive industry has pushed their cost down dramatically.

Applications

The Wii Remote for the Nintendo Wii console contains accelerometers for measuring movement and tilt to complement its pointer functionality.

Within the last several years, Nike, Polar and other companies have produced and marketed sports watches for runners that include footpods, containing accelerometers to help determine the speed and distance for the runner wearing the unit.

More recently, Apple Computer and Nike have combined the footpod, with Apple's iPod nano to provide real-time audio feedback to the runner on his/her pace and distance. It is known as the Nike + iPod Sports kit.

A small number of modern notebook computers feature accelerometers to automatically align the screen depending on the direction the device is held. This feature is only relevant in Tablet PCs and smartphones, including the iPhone.

Some laptops' hard drives utilize an accelerometer to detect when falling occurs. When low-g condition is detected, indicating a free-fall and an expected shock, the write current is turned off so that data on other tracks is not corrupted. When the free-fall and shock ends, the data can be rewritten to the desired track, thus negating the effects of the shock.

Camcorders use accelerometers for image stabilization.

Still cameras use accelerometers for anti-blur capturing. The camera holds off snapping the CCD "shutter" when the camera is moving. When the camera is still (if only for a millisecond, as could be the case for vibration), the CCD is "snapped."

Some digital cameras contain accelerometers to determine the orientation of the photo being taken and some also for rotating the current picture when viewing.

The Segway and balancing robots use accelerometers for balance.

See also

• Speed and Velocity

References

ISBN links support NWE through referral fees

• Cutnell, John D., and Kenneth W. Johnson. Physics. 7th ed. Hoboken, NJ: John Wiley, 2006. ISBN 0471663158
• Halliday, David, Robert Resnick, and Jearl Walker. Fundamentals of Physics. 7th ed. Hoboken, NJ: John Wiley, 2005. ISBN 978-0471216438
• Kuhn, Karl F. Basic Physics: A Self-Teaching Guide. 2nd ed. Hoboken, NJ: John Wiley, 1996. ISBN 0471134473
• Serway, Raymond A., and John W. Jewett. Physics for Scientists and Engineers. 6th ed. St. Paul, MN: Brooks/Cole, 2004. ISBN 0534408427
• Tipler, Paul. Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics. 5th ed. New York: W. H. Freeman, 2004. ISBN 0716708094

External links

All links retrieved June 14, 2023.

• Physics Classroom: Acceleration
• Acceleration Calculator

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Acceleration  ^history
• Accelerometer  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Acceleration"

Note: Some restrictions may apply to use of individual images which are separately licensed.