Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space (usually a Euclidean space) in a way that relates to the radius of curvature of circles that touch the object, and intrinsic curvature, which is defined at each point in a differential manifold. This article deals primarily with the first concept.

The primordial example of extrinsic curvature is that of a circle, which has curvature equal to the inverse of its radius everywhere. Smaller circles bend more sharply, and hence have higher curvature. The curvature of a smooth curve is defined as the curvature of its osculating circle at each point.

In a plane, this is a scalar quantity, but in three or more dimensions it is described by a curvature vector that takes into account the direction of the bend as well as its sharpness. The curvature of more complex objects (such as surfaces or curved, n-dimensional spaces) is described by more complex objects from linear algebra, such as the general Riemann curvature tensor.

The remainder of this article discusses some geometric examples of curvature: the curvature of a curve embedded in a plane and the curvature of a surface in Euclidean space.

One dimension in two dimensions: Curvature of plane curves

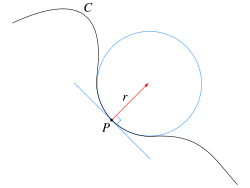
For a plane curve C, the curvature at a given point P has a magnitude equal to the reciprocal of the radius of an osculating circle (a circle that "kisses" or closely touches the curve at the given point, its center shaping the curve's evolute), and is a vector pointing in the direction of that circle's center. The smaller the radius r of the osculating circle, the larger the magnitude of the curvature (1/r) will be; so that where a curve is "nearly straight," the curvature will be close to zero, and where the curve undergoes a tight turn, the curvature will be large in magnitude.

The magnitude of curvature at points on physical curves can be measured in diopters (also spelled dioptre); a diopter has the dimension length^-1.

A straight line has curvature 0 everywhere; a circle of radius r has curvature 1/r everywhere.

Local expressions

For a plane curve given parametrically as $c(t)=(x(t),y(t))$ the curvature is

$F[x,y]={\frac {x'y''-y'x''}{(x'^{2}+y'^{2})^{3/2}}}$

For the less general case of a plane curve given explicitly as $y=f(x)$ the curvature is

$\kappa ={\frac {y''}{(1+y'^{2})^{3/2}}}$

This quantity is common in physics and engineering; for example, in the equations of bending in beams, the 1D vibration of a tense string, approximations to the fluid flow around surfaces (in aeronautics), and the free surface boundary conditions in ocean waves. In such applications, the assumption is almost always made that the slope is small compared with unity, so that the approximation:

$\kappa \approx {\frac {d^{2}y}{dx^{2}}}$

may be used. This approximation yields a straightforward linear equation describing the phenomenon, which would otherwise remain intractable.

If a curve is defined in polar coordinates as $r(\theta )$, then its curvature is

$\kappa (\theta )={\frac {r^{2}+2r'^{2}-rr''}{\left(r^{2}+r'^{2}\right)^{3/2}}}$

where here the prime refers to differentiation with respect to $\theta$.

Example

Consider the parabola $y=x^{2}$. We can parametrize the curve simply as $c(t)=(t,t^{2})=(x,y)$,

${\dot {x}}=1,\quad {\ddot {x}}=0,\quad {\dot {y}}=2t,\quad {\ddot {y}}=2.$

Substituting

$\kappa (t)=\left|{\frac {{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}}{({{\dot {x}}^{2}+{\dot {y}}^{2})}^{3/2}}}\right|={1\cdot 2-(2t)(0) \over (1+(2t)^{2})^{3/2}}={2 \over (1+4t^{2})^{3/2}}.$

One dimension in three dimensions: Curvature of space curves

For a parametrically defined space curve, the curvature is:

$F[x,y,z]={\frac {\sqrt {(z''y'-y''z')^{2}+(x''z'-z''x')^{2}+(y''x'-x''y')^{2}}}{(x'^{2}+y'^{2}+z'^{2})^{3/2}}}$

Given a function r(t) with values in R³, the curvature at a given value of $t$ is

$\kappa ={\frac {|{\dot {r}}\times {\ddot {r}}|}{|{\dot {r}}|^{3}}}$

where ${\dot {r}}$ and ${\ddot {r}}$ correspond to the first and second derivatives of r(t), respectively.

Two dimensions: Curvature of surfaces

In contrast to curves, which do not have intrinsic curvature, but do have extrinsic curvature (they only have a curvature given an embedding), surfaces have intrinsic curvature, independent of an embedding.

For a two-dimensional surface embedded in R³, consider the intersection of the surface with a plane containing the normal vector and one of the tangent vectors at a particular point. This intersection is a plane curve and has a curvature. This is the normal curvature, and it varies with the choice of the tangent vector. The maximum and minimum values of the normal curvature at a point are called the principal curvatures, k₁ and k₂, and the directions of the corresponding tangent vectors are called principal directions.

Here we adopt the convention that a curvature is taken to be positive if the curve turns in the same direction as the surface's chosen normal, otherwise negative.

The Gaussian curvature, named after Carl Friedrich Gauss, is equal to the product of the principal curvatures, k₁k₂. It has the dimension of 1/length² and is positive for spheres, negative for one-sheet hyperboloids and zero for planes. It determines whether a surface is locally convex (when it is positive) or locally saddle (when it is negative).

The above definition of Gaussian curvature is extrinsic in that it uses the surface's embedding in R³, normal vectors, external planes etc. Gaussian curvature is however in fact an intrinsic property of the surface, meaning it does not depend on the particular embedding of the surface; intuitively, this means that ants living on the surface could determine the Gaussian curvature. Formally, Gaussian curvature only depends on the Riemannian metric of the surface. This is Gauss' celebrated Theorema Egregium, which he found while concerned with geographic surveys and mapmaking.

An intrinsic definition of the Gaussian curvature at a point P is the following: imagine an ant which is tied to P with a short thread of length r. He runs around P while the thread is completely stretched and measures the length C(r) of one complete trip around P. If the surface were flat, he would find C(r) = 2πr. On curved surfaces, the formula for C(r) will be different, and the Gaussian curvature K at the point P can be computed as

$K=\lim _{r\rightarrow 0}(2\pi r-{\mbox{C}}(r))\cdot {\frac {3}{\pi r^{3}}}$

The integral of the Gaussian curvature over the whole surface is closely related to the surface's Euler characteristic; see the Gauss-Bonnet theorem.

The discrete analog of curvature, corresponding to curvature being concentrated at a point and particularly useful for polyhedra, is the (angular) defect; the analog for the Gauss-Bonnet theorem is Descartes' theorem on total angular defect.

Because curvature can be defined without reference to an embedding space, it is not necessary that a surface be embedded in a higher dimensional space in order to be curved. Such an intrinsically curved two-dimensional surface is a simple example of a Riemannian manifold.

The mean curvature is equal to the sum of the principal curvatures, k₁+k₂, over 2. It has the dimension of 1/length. Mean curvature is closely related to the first variation of surface area, in particular a minimal surface like a soap film has mean curvature zero and soap bubble has constant mean curvature. Unlike Gauss curvature, the mean curvature is extrinsic and depends on the embedding, for instance, a cylinder and a plane are locally isometric but the mean curvature of a plane is zero while that of a cylinder is nonzero.

Three dimensions: Curvature of space

By extension of the former argument, a space of three or more dimensions can be intrinsically curved; the full mathematical description is described at curvature of Riemannian manifolds. Again, the curved space may or may not be conceived as being embedded in a higher-dimensional space. In recent physics jargon, the embedding space is known as the bulk and the embedded space as a p-brane where p is the number of dimensions; thus a surface (membrane) is a 2-brane; normal space is a 3-brane etc.

After the discovery of the intrinsic definition of curvature, which is closely connected with non-Euclidean geometry, many mathematicians and scientists questioned whether ordinary physical space might be curved, although the success of Euclidean geometry up to that time meant that the radius of curvature must be astronomically large. In the theory of general relativity, which describes gravity and cosmology, the idea is slightly generalized to the "curvature of space-time"; in relativity theory space-time is a pseudo-Riemannian manifold. Once a time coordinate is defined, the three-dimensional space corresponding to a particular time is generally a curved Riemannian manifold; but since the time coordinate choice is largely arbitrary, it is the underlying space-time curvature that is physically significant.

Although an arbitrarily-curved space is very complex to describe, the curvature of a space which is locally isotropic and homogeneous is described by a single Gaussian curvature, as for a surface; mathematically these are strong conditions, but they correspond to reasonable physical assumptions (all points and all directions are indistinguishable). A positive curvature corresponds to the inverse square radius of curvature; an example is a sphere or hypersphere. An example of negatively curved space is hyperbolic geometry. A space or space-time without curvature (formally, with zero curvature) is called flat. For example, Euclidean space is an example of a flat space, and Minkowski space is an example of a flat space-time. There are other examples of flat geometries in both settings, though. A torus or a cylinder can both be given flat metrics, but differ in their topology. Other topologies are also possible for curved space. See also shape of the universe.

See also

• Circle
• Curve
• Ellipse

External links

All links retrieved January 12, 2024.

• 3D-XplorMath Java applets Applets for space curves with osculating circles.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Curvature  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Curvature"

Note: Some restrictions may apply to use of individual images which are separately licensed.