Spacetime

Three-dimensional analogy of space-time distortion. Matter changes the geometry of spacetime, this (curved) geometry being interpreted as gravity. White lines do not represent the curvature of space, but instead represent the coordinate system imposed on the curved spacetime which would be rectilinear in a flat spacetime.

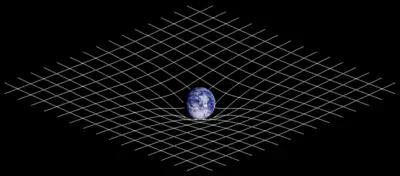
In classical physics, space and time are assumed to be quite different. This agrees with our everyday experience, the commonsense difference between our experience of time and space. Modern physics tells us that this difference is an illusion, that time cannot be separated from the three dimensions of space, a phenomenon that becomes apparent for observers traveling at very high speeds. The three dimensions of space and the one dimension of time combine into a single four-dimensional manifold, called the space-time continuum.

The basic property of spacetime is 'the metric' that describes the separation between two events. The metric is just an extension of the Pythagorean Theorem, with x, y and z being the space components and "ict" being the time component (where i is the imaginary unit, or square root of -1; t is the time; and c is the speed of light). As the square of i is -1, time enters the Pythagorean relation as a negative number. The factor c enters to convert time units (such as seconds) into the same units as space (such as miles). Moving through a second of time is equivalent to moving almost 200,000 miles in space.

The spacetime separation is an invariant. Although two observers moving at relativistic speeds will disagree about the length and duration of an event, when they calculate the spacetime separation using the Pythagorean relation—the square root of the sum of the squares—they will come up with the same invariant number.

Origin

The space and time dimensions of spacetime seem to have had different histories.

The spatial extent of the universe is thought to have been created in period of cosmic inflation of the false vacuum that occurred a moment before the hot Big Bang, when the universe doubled in size about a hundred times with each quantum tick of Planck time. This exponential inflation over a few ticks of time stretched space from smaller than a proton to larger than the current visible universe. The abrupt ending to this initiated the hot big bang and the creation of the universe. The expansion of space continued at a much more sedate space, the expansion since inflation is minor in comparison.

The hot Big Bang involved such a high temperature that even the most massive of particles were moving at essentially the speed of light. Special relativity states that when moving at c through space is motionless in time. The extension into the time dimension only got going when things had cooled down enough for particles to slow down in space and speed up in time. The proper time of the universe is defined to be that of a reference frame moving with essentially zero velocity, relative to c, to the cosmic background microwave radiation. This holds for just about everything in this age of the universe which is why time seemed to be a constant to the classical scientists.

Concept with dimensions

According to Euclidean space perception, the universe has three dimensions of space, and one dimension of time. By combining space and time into a single manifold, physicists have significantly simplified a large amount of physical theory, as well as described in a more uniform way the workings of the universe at both the supergalactic and subatomic levels.

In classical mechanics, time is treated as a constant, being independent of mechanical motion in three dimensions (which matches reality at low speeds). In relativistic contexts, however, time cannot be separated from the three dimensions of space because it depends on an object's velocity relative to the speed of light, and also the strength of intense gravitational fields which can slow the passage of time.

The concept of spacetime combines space and time within a single coordinate system, typically with 4 dimensions: length, width, height, and time. Dimensions are components of a coordinate grid typically used to locate a point in space, or on the globe, such as by latitude, longitude and planet (Earth). However, with spacetime, the coordinate grid is used to locate "events" (rather than just points in space), so time is added as another dimension to the grid.

Formerly, from experiments at slow speeds, time was believed to be a constant, which progressed at a fixed rate; however, later high-speed experiments revealed that time slowed down at higher speeds (with such slowing called "time dilation"). Many experiments have confirmed the slowing from time dilation, such as atomic clocks onboard a Space Shuttle running slower than synchronized Earth-bound clocks. Since time varies, it is treated as a variable within the spacetime coordinate grid, and time is no longer assumed to be a constant, independent of the location in space.

Note that the treatment of spacetime events with the 4 dimensions (including time) is the conventional view. However, other invented coordinate grids treat time as having 3 additional dimensions—with length-time, width-time, and height-time—to accompany the 3 dimensions of space. When dimensions are understood as mere components of the grid system, rather than physical attributes of space, it is easier to understand the alternate dimensional views, such as: latitude, longitude, plus Greenwich Mean Time (3 dimensions), or city, state, postal code, country, and UTC time (5 dimensions). The various dimensions are chosen, depending on the coordinate grid used.

The term spacetime has taken on a generalized meaning with the advent of higher-dimensional theories. How many dimensions are needed to describe the universe is still an open question. Speculative theories such as string theory predict 10 or 26 dimensions (with M-theory predicting 11 dimensions; 10 spatial and 1 temporal), but the existence of more than four dimensions would only appear to make a difference at the subatomic level.

Historical origin

The origins of this twentieth century scientific concept began in the nineteenth century with fiction writers. Edgar Allan Poe stated in his essay on cosmology titled Eureka (1848) that "Space and duration are one." This is the first known instance of suggesting space and time to be different perceptions of one thing. Poe arrived at this conclusion after approximately 90 pages of reasoning but employed no mathematics. In 1895, in his novel, The Time Machine, H.G. Wells wrote, “There is no difference between time and any of the three dimensions of space except that our consciousness moves along it.” He added, “Scientific people … know very well that time is only a kind of space.”

While spacetime can be viewed as a consequence of Albert Einstein's 1905 theory of special relativity, it was first explicitly proposed mathematically by one of his teachers, the mathematician Hermann Minkowski, in a 1908 essay building on and extending Einstein's work. His concept of Minkowski space is the earliest treatment of space and time as two aspects of a unified whole, the essence of special relativity. The idea of Minkowski Space also led to special relativity being viewed in a more geometrical way, this geometric viewpoint of spacetime being important in general relativity too. (For an English translation of Minkowski's article, see Lorentz et al. 1952.) The 1926 thirteenth edition of the Encyclopedia Britannica included an article by Einstein titled "space-time."

Basic concepts

Spacetimes are the arenas in which all physical events take place—an event is a point in spacetime specified by its time and place. For example, the motion of planets around the Sun may be described in a particular type of spacetime, or the motion of light around a rotating star may be described in another type of spacetime. The basic elements of spacetime are events. In any given spacetime, an event is a unique position at a unique time. Examples of events include the explosion of a star or the single beat of a drum.

A spacetime is independent of any observer. However, in describing physical phenomena (which occur at certain moments of time in a given region of space), each observer chooses a convenient coordinate system. Events are specified by four real numbers in any coordinate system. The worldline of a particle or light beam is the path that this particle or beam takes in the spacetime and represents the history of the particle or beam. The worldline of the orbit of the Earth is depicted in two spatial dimensions x and y (the plane of the Earth orbit) and a time dimension orthogonal to x and y. The orbit of the Earth is an ellipse in space alone, but its worldline is a helix in spacetime.

The unification of space and time is exemplified by the common practice of expressing distance in units of time, by dividing the distance measurement by the speed of light.

Space-time intervals

Spacetime entails a new concept of distance. Whereas distances are always positive in Euclidean spaces, the distance between any two events in spacetime (called an "interval") may be real, zero, or even imaginary. The spacetime interval quantifies this new distance (in Cartesian coordinates $x,y,z,t$):

$s^{2}=\,c^{2}t^{2}-r^{2}$

where $c$ is the speed of light, differences of the space and time coordinates of the two events are denoted by $r$ and $t$, respectively and $r^{2}=x^{2}+y^{2}+z^{2}$. (Note that the choice of signs above follows the Landau-Lifshitz spacelike convention. Other treatments reverse the order of the arguments on the right-hand side. If this alternate convention is chosen, the relationships in the next two paragraphs are reversed.)

Pairs of events in spacetime may be classified into 3 distinct types based on 'how far' apart they are:

• time-like (more than enough time passes for there to be a cause-effect relationship between the two events; there exists a reference frame such that the two events occur at the same place; $s^{2}>0$).
• light-like (the space between the two events is exactly balanced by the time between the two events; $s^{2}=0$).
• space-like (not enough time passes for there to be a cause-effect relationship between the two events; there exists a reference frame such that the two events occur at the same time; $s^{2}<0$).

Events with a positive spacetime interval are in each other's future or past, and the value of the interval defines the proper time measured by an observer traveling between them. Events with a spacetime interval of zero are separated by the propagation of a light signal.

For special relativity, the spacetime interval is considered invariant across inertial reference frames.

Certain types of worldlines (called geodesics of the spacetime) are the shortest paths between any two events, with distance being defined in terms of spacetime intervals. The concept of geodesics becomes critical in general relativity, since geodesic motion may be thought of as "pure motion" (inertial motion) in spacetime, that is, free from any external influences.

Mathematics of space-times

For physical reasons, a space-time continuum is mathematically defined as a four-dimensional, smooth, connected pseudo-Riemannian manifold together with a smooth Lorentz metric of signature $\left(3,1\right)$. The metric determines the geometry of spacetime, as well as determining the geodesics of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates $\left(x,y,z,t\right)$ are used. Moreover, for simplicity's sake, the speed of light 'c' is usually assumed to be unity.

A reference frame (observer) can be identified with one of these coordinate charts; any such observer can describe any event $p$. Another reference frame may be identified by a second coordinate chart about $p$. Two observers (one in each reference frame) may describe the same event $p$ but obtain different descriptions.

Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing $p$ (representing an observer) and another containing $q$ (another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as 'local observers who can perform measurements in their vicinity' also makes good physical sense, as this is how one actually collects physical data - locally.

For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event $p$). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples $\left(x,y,z,t\right)$ (as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.

Geodesics are said to be timelike, null, or spacelike if the tangent vector to one point of the geodesic is of this nature. The paths of particles and light beams in spacetime are represented by timelike and null (light-like) geodesics (respectively).

Topology

The assumptions contained in the definition of a spacetime are usually justified by the following considerations.

The connectedness assumption serves two main purposes. First, different observers making measurements (represented by coordinate charts) should be able to compare their observations on the non-empty intersection of the charts. If the connectedness assumption were dropped, this would not be possible. Second, for a manifold, the property of connectedness and path-connectedness are equivalent and one requires the existence of paths (in particular, geodesics) in the spacetime to represent the motion of particles and radiation.

Every spacetime is paracompact. This property, allied with the smoothness of the spacetime, gives rise to a smooth linear connection, an important structure in general relativity. Some important theorems on constructing spacetimes from compact and non-compact manifolds include the following:

• A compact manifold can be turned into a spacetime if, and only if, its Euler characteristic is 0.
• Any non-compact 4-manifold can be turned into a spacetime.

Space-time symmetries

Often in relativity, space-times that have some form of symmetry are studied. As well as helping to classify spacetimes, these symmetries usually serve as a simplifying assumption in specialized work. Some of the most popular ones include:

• Axially symmetric spacetimes
• Spherically symmetric spacetimes
• Static spacetimes
• Stationary spacetimes

The causal structure of a spacetime describes causal relationships between pairs of points in the spacetime based on the existence of certain types of curves joining the points.

Spacetime in special relativity

The geometry of spacetime in special relativity is described by the Minkowski metric on R⁴. This spacetime is called Minkowski space. The Minkowski metric is usually denoted by $\eta$ and can be written as a four-by-four matrix:

$\eta _{ab}\,=\operatorname {diag} (1,-1,-1,-1)$

where the Landau-Lifshitz spacelike convention is being used. (Here it is space that is measured by an imaginary number while time is real.) A basic assumption of relativity is that coordinate transformations must leave spacetime intervals invariant. Intervals are invariant under Lorentz transformations. This invariance property leads to the use of four-vectors (and other tensors) in describing physics.

Strictly speaking, one can also consider events in Newtonian physics as a single spacetime. This is Galilean-Newtonian relativity, and the coordinate systems are related by Galilean transformations. However, since these preserve spatial and temporal distances independently, such a space-time can be decomposed into spatial coordinates plus temporal coordinates, which is not possible in the general case.

Spacetime in general relativity

In general relativity, it is assumed that spacetime is curved by the presence of matter (energy), this curvature being represented by the Riemann tensor. In special relativity, the Riemann tensor is identically zero, and so this concept of "non-curvedness" is sometimes expressed by the statement "Minkowski spacetime is flat."

Many space-time continua have physical interpretations which most physicists would consider bizarre or unsettling. For example, a compact spacetime has closed, time-like curves, which violate our usual ideas of causality (that is, future events could affect past ones). For this reason, mathematical physicists usually consider only restricted subsets of all the possible spacetimes. One way to do this is to study "realistic" solutions of the equations of general relativity. Another way is to add some additional "physically reasonable" but still fairly general geometric restrictions, and try to prove interesting things about the resulting spacetimes. The latter approach has led to some important results, most notably the Penrose-Hawking singularity theorems.

Quantized space-time

In general relativity, space-time is assumed to be smooth and continuous- and not just in the mathematical sense. In the theory of quantum mechanics, there is an inherent discreteness present in physics. In attempting to reconcile these two theories, it is sometimes postulated that spacetime should be quantized at the very smallest scales. Current theory is focused on the nature of space-time at the Planck scale. In this sense, spacetime comes in pixels with Planck length and time size. Causal sets, loop quantum gravity, string theory, and black hole thermodynamics all predict a quantized space-time with agreement on the order of magnitude. Loop quantum gravity makes precise predictions about the geometry of spacetime at the Planck scale.

Privileged character of 3+1 spacetime

A number of scientists and philosophers have written about spacetime, and concepts have evolved as more theories have been deduced and tested by mathematical analysis or experimentation.

Also the subject of spacetime has been a topic for pseudo-intellectuals, espousing their views in attempts to impress others, regardless of matching any experimental data.

Other writers have been limited by the scientific evidence available at the time. For example, in the latter twentieth century, experiments with "atom-smasher" particle accelerators had revealed that individual protons accelerated to high speeds were gaining the mass equivalent to a car at rest, requiring ever-increasing amounts of energy to accelerate the protons even faster. While the passage of Time slowed at high speeds, the mass of the particles increased. Writers from previous eras were not aware of that evidence, so fanciful views are sometimes expressed in the writings that are described below.

Let dimensions be of two kinds: spatial and temporal. That spacetime, ignoring any undetectable compactified dimensions, consists of three spatial (bidirectional) and one temporal (unidirectional) dimensions can be explained by appealing to the physical consequences of differing numbers of dimensions. The argument is often of an anthropic nature.

Immanuel Kant argued that 3-dimensional Space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow says of it that "we would regard this as getting the punch-line back to front: it is the three-dimensionality of Space that explains why we see inverse-square force laws in Nature, not vice-versa" (Barrow 2002). This is because the law of gravitation (or any other inverse-square law) follows from the concept of flux, from Space having 3 dimensions, and from 3-dimensional solid objects having surface area proportional to the square of their size in one chosen dimension. In particular, a sphere of radius r has area of 4πr². More generally, in a Space of N dimensions, the strength of the gravitational attraction between two bodies separated by a distance of r would be inversely proportional to r^N-1.

Fixing the number of temporal dimensions at 1 and letting the number of spatial dimensions N exceed 3, Paul Ehrenfest showed in 1920 that the orbit of a planet about its sun cannot remain stable, and that the same holds for a star's orbit around its galactic center. Likewise, F.R. Tangherlini showed in 1963 that when N>3, electrons would not form stable orbitals around nuclei; they would either fall into the nucleus or disperse. Ehrenfest also showed that if N is even, then the different parts of a wave impulse will travel at different speeds. If N is odd and greater than 3, wave impulses become distorted. Only when N=3 or 1 are both problems avoided.

Tegmark expands on the preceding argument in the following anthropic manner. If the number of Time dimensions differed from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. In addition, Tegmark maintains that protons and electrons would be unstable in a universe with more than one Time dimension, as they can decay into more massive particles (this is not a problem if the temperature is sufficiently low). If N>3, Ehrenfest's above argument holds: atoms as we know them (and probably more complex structures as well) could not exist. If N<3, gravitation of any kind becomes problematic, and the universe is probably too simple to contain observers. For example, nerves must intersect and cannot overlap.

In general, it is not clear how physical laws could operate if the number of Time dimensions T differed from 1. If T>1, individual subatomic particles which decay after a fixed period would not have much predictability because timelike geodesics would not be necessarily maximal. N=1 and T=3 has the peculiar property that that the speed of light in a vacuum is a lower bound on the velocity of matter. Hence anthropic arguments rule out all cases except 3 spatial and 1 temporal dimensions, which describes the world we live in.

Curiously, 3 and 4 dimensional spaces appear richest geometrically and topologically. For example, there are geometric statements whose truth or falsity is known for any number of spatial dimensions except 3, 4, or both.

For a more detailed introduction to the privileged status of 3 spatial and 1 temporal dimensions, see Barrow; for a deeper treatment, see Barrow and Tipler. Barrow regularly cites Whitrow.

In string theory, physicists are not constrained by notions limited to 3+1 dimensions, so coordinate grids of 10, or perhaps 26 dimensions, are used to describe the types and locations of the vibrating strings. String theory follows the notion that the "universe is wiggly" and considers matter and energy to be composed of tiny vibrating strings of various types, specified by some of the dimensions.

References

ISBN links support NWE through referral fees

• Barrow, J.D. The Constants of Nature. New York, NY: Pantheon Books, 2002. ISBN 0375422218.
• Barrow, J.D., and Frank J. Tipler. The Anthropic Cosmological Principle. Oxford, UK: Oxford University Press, 1986. ISBN 0198519494.
• Ehrenfest, Paul. How do the fundamental laws of physics make manifest that Space has 3 dimensions? Annalen der Physik 61 (1920):440.
• Gal-Or, Benjamin. Cosmology, Physics and Philosophy. New York, NY: Springer Verlag, 1983.
• Kant, Immanuel. J. Handyside (trans.). "Thoughts on the true estimation of living forces." Kant's Inaugural Dissertation and Early Writings on Space. London,UK: The Open court publishing company, 1929.
• Lorentz, H.A., Albert Einstein, Hermann Minkowski, and Hermann Weyl. The Principle of Relativity: A Collection of Original Memoirs. London, UK: Methuen & Co. Ltd., 1952.
• Lucas, John Randolph. A Treatise on Time and Space. London, UK: Methuen, 1973. ISBN 0416750702.
• Matolcsi, Tamás. Spacetime Without Reference Frames. Budapest, HU: Akadémiai Kiadó, 1994.
• Minkowski, Hermann. "Raum und Zeit. Versammlung Deutscher Naturforscher." Physikalische Zeitschrift 10 (1908): 104-111.
• Penrose, Roger. The Road to Reality. London, UK: Jonathan Cape, 2004. ISBN 0224044478.
• Poe, Edgar A. Eureka; An Essay on the Material and Spiritual Universe. London, UK: Hesperus Press Limited, 1848. ISBN 1843910098.
• Robb, A.A. Geometry of Time and Space. Cambridge, UK: University Press, 1936.
• Schutz, J.W. Independent axioms for Minkowski Space-time. Addison-Wesley Longman, 1997. ISBN 0582317606.
• Tangherlini, F.R. Atoms in Higher Dimensions. Nuovo Cimento. 14(27) (1963):636.
• Taylor, E.F. and John A. Wheeler. Spacetime Physics. San Francisco, CA: W.H. Freeman, 1966.
• Wells, H.G. The Time Machine. New York, NY: Pocket Books, 2004. ISBN 0743487737.
• Whitrow, James Gerald. The Structure and Evolution of the Universe. London, UK: Hutchinson, 1959.

External links

All links retrieved February 7, 2023.

• SpaceTime, Relativity, and Quantum Physics
• Einstein Minkowski Space-Time Diagram

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Spacetime  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Spacetime"

Note: Some restrictions may apply to use of individual images which are separately licensed.