Dimension

Left to right: the square has two dimensions, the cube has three, and the tesseract has four.

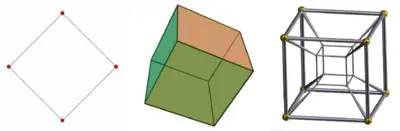
In common usage, dimension (from Latin dimensio, meaning "measured out") is a parameter or measure of spatial characteristics of an object, such as length, width, and height. In mathematics, the dimensions of an object (or collection of objects) in space is roughly defined as the minimum number of coordinates needed to specify every point within that object (or collection). Thus, an idealized point (with a thickness of zero or nearly zero) has a dimension of zero, a line segment has one dimension, a square has two dimensions, a cube has three, and a tesseract has four.

For some calculations, time may be added as a third dimension to two-dimensional (2D) space or a fourth dimension to three-dimensional (3D) space. The dimensions of time and space are required when attempting to locate the time and place of an event.

The concept of dimensions has been extended to different fields of study, in which spaces are defined by their own relevant dimensions. In geographical space models, the units of dimensions may be meters or feet; in economic models, the units may include cost or price.

Dimensions play a fundamental role in our perception of the world around us. Immanuel Kant noted that we do not actually perceive these dimensions, but they form the framework in which we perceive events; they form the a priori background in which events are perceived.

Examples

Locating a city on a map of the Earth requires two parameters: latitude and longitude. The map is therefore said to have "two dimensions" in space. Alternatively, the map is said to be 2-dimensional (or 2D), or its dimension is said to be two.

Locating the exact position of an aircraft in flight (relative to a reference position on the Earth) requires another dimension, altitude. Hence the position of the aircraft can be rendered in three-dimensional space (3D). By adding the three Euler angles for a total 6 dimensions, it is possible to determine the orientation and trajectory of the aircraft as well.

In the case of an aircraft, its estimated "speed" may be calculated from a comparison between the times associated with any two positions. For common uses, simply using "speed" (as a dimension) is a useful way of condensing (or translating) the more abstract time dimension, even if "speed" is not a dimension but is a calculation based on two dimensions. (Actually, it is possible and useful to consider "spaces" with extra dimensions for representing velocity, because it helps solve certain equations.)

Some theoretical physicists study unusual conceptual models of space by adding extra dimensions or changing their properties. This approach has helped describe concepts in quantum mechanics—that is, the 'physics beneath the visible physical world.' The concept of multiple dimensions has been borrowed by science fiction writers as a metaphorical device, where an "alternate dimension" (such as an 'alternate universe' or 'plane of existence') describes extraterrestrial places, species, and cultures that function in ways that are different and unusual compared to human culture.

In physics

Spatial dimensions

A three-dimensional Cartesian coordinate system.

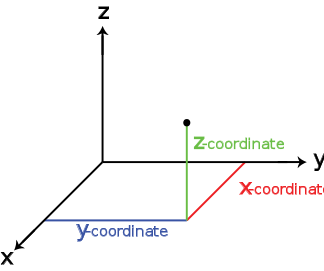
Classical physics theories describe objects in three spatial dimensions. These dimensions can be thought of as three axes in a Cartesian coordinate system, which run left-right, up-down, and forward-backward. A set of three coordinates on these axes, or any other three-dimensional coordinate system, specifies the position of a particular point in space.

Likewise, the basic directions of movement of an object are up/down, left/right, and forward/backward. Movement in any other direction can be expressed in terms of just these three. Moving down is the same as moving up a negative amount. Moving diagonally upward and forward is just as the name of the direction implies; that is, moving in a linear combination of up and forward. In its simplest form: a line describes one dimension, a plane describes two dimensions, and a cube describes three dimensions.

In the physical world, according to the theory of relativity the fourth dimension is time, which runs before-after. An event’s position in space and time is therefore specified if four co-ordinates are given.

On surfaces such as a plane or the surface of a sphere, a point can be specified using just two numbers and so this space is said to be two-dimensional. Similarly a line is one-dimensional because only one coordinate is needed, whereas a point has no dimensions.

Time

Time is often referred to as the "fourth dimension." It is, in essence, one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that movement seems to occur at a fixed rate and in one direction.

The equations used in physics to model reality often do not treat time in the same way that humans perceive it. In particular, the equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).

The best-known treatment of time as a dimension is Poincaré and Einstein's special relativity (and extended to general relativity), which treats perceived space and time as parts of a four-dimensional manifold.

Additional dimensions

Some theories, such as string theory and M-theory, postulate that space in general has 10 or 11 dimensions, but that the universe, when measured along these additional dimensions, is subatomic in size. As a result, we perceive only the three spatial dimensions that have macroscopic size. We as humans can only perceive up to the third dimension while we have knowledge of our travel through the fourth. We cannot, however, see anything past the fourth.

Penrose's singularity theorem

In his book The Road to Reality: A Complete Guide to the Laws of the Universe, scientist Sir Roger Penrose explained his singularity theorem. It asserts that all theories that attribute more than three spatial dimensions and one temporal dimension to the world of experience are unstable. The instabilities that exist in systems of such extra dimensions would result in their rapid collapse into a singularity. For that reason, Penrose wrote, the unification of gravitation with other forces through extra dimensions cannot occur.

Units

In the physical sciences and engineering, the dimension of a physical quantity is the expression of the class of physical unit that such a quantity is measured against. An example of a dimension is length (L), which is the dimension for measurements expressed in units of length, such as meters, nautical miles, or lightyears. Another example is time (T), which is expressed in units such as seconds or hours.

In general, physical measurements that must be expressed in units of measurement, and quantities obtained by such measurements, are said to be "dimensionful." Speed, which is the distance (length) traveled in a certain amount of time, is a dimensionful quantity that has the dimension LT ⁻¹ (meaning L/T). Acceleration, the change in speed per time unit, has the dimension LT ⁻².

In mathematics

Mathematicians use the term manifold in a generic sense to mean the area of a surface, volume of a body, and so forth. Based on that term, the number of dimensions of a manifold is equal to the lowest integer number of coordinates needed to specify the position of each point in the manifold. For example, one number is needed to specify the position of a point on a line; two numbers are needed to specify the position of a point on a surface.

Yet, no definition of dimension adequately captures the concept in all situations in which we would like to use it. Consequently, mathematicians have devised numerous definitions of dimension for different types of spaces. All, however, are ultimately based on the concept of the dimension of Euclidean n-space E ⁿ. The point E ⁰ is 0-dimensional. The line E ¹ is 1-dimensional. The plane E ² is 2-dimensional. And in general E ⁿ is n-dimensional.

A tesseract is an example of a four-dimensional object. Whereas outside of mathematics the use of the term "dimension" is as in: "A tesseract has four dimensions," mathematicians usually express this as: "The tesseract has dimension 4," or: "The dimension of the tesseract is 4."

The rest of this section examines some of the more important mathematical definitions of dimension.

Manifolds

In mathematics, spaces with more than three dimensions are used to describe other manifolds. In n-dimensional space, a point is located by n coordinates (x₁, x₂, … x_n). Some theories, such as those used in fractal geometry, make use of non-integer and negative dimensions.

The theory of manifolds, in the field of geometric topology, is characterized by the way in which dimensions 1 and 2 are relatively elementary; the "high-dimensional" cases of n > 4 are simplified by having extra space in which to 'work'; and the cases n = 3 and 4 are in some senses the most difficult.

Hamel dimension

The dimension of a vector space V is the cardinality (that is, the number of vectors) of a basis of V. It is sometimes called Hamel dimension or algebraic dimension, to distinguish it from other types of dimension. All bases of a vector space have equal cardinality, and therefore the dimension of a vector space is uniquely defined.

Lebesgue covering dimension

For any topological space, the Lebesgue covering dimension is defined to be n if n is the smallest integer for which the following holds: any open cover has a refinement (a second cover where each element is a subset of an element in the first cover) such that no point is included in more than n + 1 elements. For manifolds, this coincides with the dimension mentioned above. If no such n exists, then the dimension is infinite.

Inductive dimension

The inductive dimension of a topological space may refer to the small inductive dimension or the large inductive dimension, and is based on the analogy that n+1-dimensional balls have n dimensional boundaries, permitting an inductive definition based on the dimension of the boundaries of open sets.

Hausdorff dimension

For sets which are of a complicated structure, especially fractals, the Hausdorff dimension is useful. The Hausdorff dimension is defined for all metric spaces and, unlike the Hamel dimension, can also attain non-integer real values. The box dimension is a variant of the same idea. In general, there exist more definitions of fractal dimensions that work for highly irregular sets and attain non-integer positive real values.

Hilbert spaces

Every Hilbert space admits an orthonormal basis, and any two such bases for a particular space have the same cardinality. This cardinality is called the dimension of the Hilbert space. This dimension is finite if and only if the space's Hamel dimension is finite, and in this case the two dimensions coincide.

Krull dimension of commutative rings

The Krull dimension of a commutative ring, named after Wolfgang Krull (1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideals in the ring.

Negative dimension

The negative (fractal) dimension is introduced by Benoit Mandelbrot, in which, when it is positive gives the known definition, and when it is negative measures the degree of "emptiness" of empty sets.

Science fiction

Science fiction texts often mention the concept of dimension, when really referring to parallel universes, alternate universes, or other planes of existence. This usage is derived from the idea that in order to travel to parallel/alternate universes/planes of existence one must travel in a spatial direction/dimension besides the standard ones. In effect, the other universes/planes are just a small distance away from our own, but the distance is in a fourth (or higher) spatial dimension, not the standard ones.

More dimensions

• Dimension of an algebraic variety
• Lebesgue covering dimension
• Isoperimetric dimension
• Poset dimension
• Metric dimension
• Pointwise dimension
• Lyapunov dimension
• Kaplan-Yorke dimension
• Exterior dimension
• Hurst exponent
• q-dimension; especially:
  • Information dimension (corresponding to q=1)
  • Correlation dimension (corresponding to q=2)

See also

• Cartesian coordinate system
• General relativity, an introduction
• Line (mathematics)
• Point (geometry)
• Space
• Spacetime
• Special relativity, an introduction
• Stereoscopy
• String theory
• Tesseract
• Time

References

ISBN links support NWE through referral fees

• Banchoff, Thomas. Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, 2nd ed. New York: Scientific American Library, Distributed by W.H. Freeman, 1990. ISBN 978-0716750253
• Fuchs, Vivian, and W. G. Richards. Oxford Illustrated Encyclopedia. Volume 1, The Physical World. Oxford: Oxford University Press, 1985.
• Penrose, Roger. The Road to Reality: A Complete Guide to the Laws of the Universe. New York: A.A. Knopf, 2005. ISBN 978-0679454434
• Pickover, Clifford A. Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons. New York: Oxford University Press, 1999. ISBN 0195130065 ISBN 978-0195130065.
• Rucker, Rudy. The Fourth Dimension. Boston: Houghton Mifflin, 1984. ISBN 0395344204

External links

All links retrieved January 29, 2024.

• Fractal Curves and Dimension.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Dimension  ^history
• Dimension  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Dimension"

Note: Some restrictions may apply to use of individual images which are separately licensed.