Square (geometry)

Square
A square The sides of a square and its diagonals meet at right angles.
Edges and vertices	4
Schläfli symbols	{4} {}x{}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D4)
Area (with t=edge length)	t2
Internal angle (degrees)	90°

In plane (Euclidean) geometry, a square is a regular polygon with four sides. It may also be thought of as a special case of a rectangle, as it has four right angles and parallel sides. Likewise, it is also a special case of a rhombus, kite, parallelogram, and trapezoid.

Mensuration formulae

The area of a square is the product of the length of its sides.

The perimeter of a square whose sides have length t is

$P=4t.$

And the area is

$A=t^{2}.$

In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.

Standard coordinates

The coordinates for the vertices of a square centered at the origin and with side length 2 are (±1, ±1), while the interior of the same consists of all points (x₀, x₁) with −1 < x_i < 1.

Properties

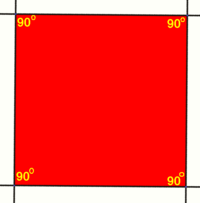
Each angle in a square is equal to 90 degrees, or a right angle.

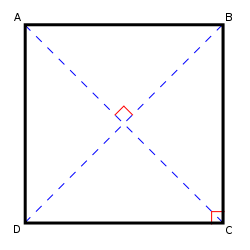
The diagonals of a square are equal. Conversely, if the diagonals of a rhombus are equal, then that rhombus must be a square. The diagonals of a square are ${\sqrt {2}}$ (about 1.41) times the length of a side of the square. This value, known as Pythagoras’ constant, was the first number proven to be irrational.

If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths) then it is a square.

Other facts

• If a circle is circumscribed around a square, the area of the circle is $\pi /2$ (about 1.57) times the area of the square.
• If a circle is inscribed in the square, the area of the circle is $\pi /4$ (about 0.79) times the area of the square.
• A square has a larger area than any other quadrilateral with the same perimeter.
• A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).
• The square is in two families of polytopes in two dimensions: hypercube and the cross polytope. The Schläfli symbol for the square is {4}.
• The square is a highly symmetric object. There are four lines of reflectional symmetry and it has rotational symmetry through 90°, 180° and 270°. Its symmetry group is the dihedral group $D_{4}$.
• If the area of a given square with side length S is multiplied by the area of a "unit triangle" (an equilateral triangle with side length of 1 unit), which is ${\tfrac {\sqrt {3}}{4}}$ units squared, the new area is that of the equilateral triangle with side length S.

Non-Euclidean geometry

In non-euclidean geometry, squares are more generally polygons with four equal sides and equal angles.

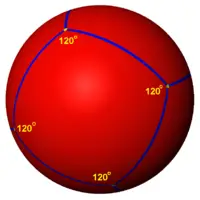
In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of plane geometry, the angles of such a square are larger than a right angle.

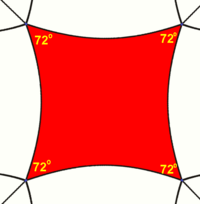
In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have angles of less than right angles. Larger squares have smaller angles.

Examples:

Six squares can tile the sphere with three squares around each vertex and 120 degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}.

Squares can tile the Euclidean plane with four around each vertex, with each square having an internal angle of 90 degrees. The Schläfli symbol is {4,4}.

Squares can tile the hyperbolic plane with five around each vertex, with each square having 72 degree internal angles. The Schläfli symbol is {4,5}.

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. New York, NY: Hungry Minds. ISBN 0764553240
• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502
• Leff, Lawrence S. 1997. Geometry the Easy Way. Hauppauge, NY: Barron’s Educational Series. ISBN 0764101102
• Stillwell, John. 2005. The Four Pillars of Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387255303

External links

All links retrieved January 1, 2020.

• Definiton and properties of a square With interactive applet.
• Animated applet illustrating the area of a square

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Square (geometry)  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Square (geometry)"

Note: Some restrictions may apply to use of individual images which are separately licensed.