Parallelogram

A parallelogram

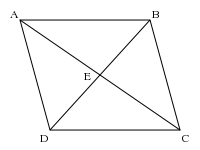
In geometry, a parallelogram is a quadrilateral with two sets of parallel sides. The opposite sides of a parallelogram are of equal length, and the opposite angles of a parallelogram are congruent. The three-dimensional counterpart of a parallelogram is a parallelepiped.

Properties

• The two parallel sides are of equal length.
• The area, $A$, of a parallelogram is $A=BH$ where $B$ is the base of the parallelogram and $H$ is its height.
• The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
• The area is also equal to the magnitude of the vector cross product of two adjacent sides.
• The diagonals of a parallelogram bisect each other.
• It is possible to create a tessellation with any parallelogram.
• The parallelogram is itself a special case of a trapezoid.

Vector spaces

In a vector space, addition of vectors is usually defined using the parallelogram law. The parallelogram law distinguishes Hilbert spaces from other Banach spaces.

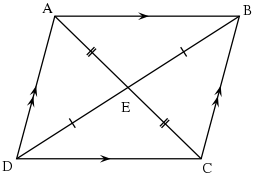
Proof that diagonals bisect each other

To prove that the diagonals of a parallelogram bisect each other, first note a few pairs of equivalent angles:

$\angle ABE\cong \angle CDE$

$\angle BAE\cong \angle DCE$

Since they are angles that a transversal makes with parallel lines $AB$ and $DC$.

Also, $\angle AEB\cong \angle CED$ since they are a pair of vertical angles.

Therefore, $\triangle ABE\sim \triangle CDE$ since they have the same angles.

From this similarity, we have the ratios

${AB \over CD}={AE \over CE}={BE \over DE}$

Since $AB=DC$, we have

${AB \over CD}=1$.

Therefore,

$AE=CE$

$BE=DE$

$E$ bisects the diagonals $AC$ and $BD$.

Derivation of the area formula

Area of the parallelogram is in blue

The area formula,

$A_{\text{parallelogram}}=B\times H,\,$

can be derived as follows:

The area of the parallelogram to the right (the blue area) is the total area of the rectangle less the area of the two orange triangles. The area of the rectangle is

$A_{\text{rect}}=(B+A)\times H\,$

and the area of a single orange triangle is

$A_{\text{tri}}={\frac {1}{2}}A\times H\,$

Therefore, the area of the parallelogram is

$A_{\text{parallelogram}}=A_{\text{rect}}-2\times A_{\text{tri}}=\left((B+A)\times H\right)-\left(A\times H\right)=B\times H\,$

See also

• Angle (mathematics)
• Line (mathematics)
• Square (geometry)

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240
• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502
• Leff, Lawrence S. 1997. Geometry the Easy Way. Hauppauge, NY: Barron’s Educational Series. ISBN 0764101102
• Stillwell, John. 2005. The Four Pillars of Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387255303

External links

All links retrieved November 18, 2022.

• Weisstein, Eric W. Parallelogram MathWorld—A Wolfram Web Resource.
• Parallelogram: Properties, Shapes, Diagonals and Area
• Parallelogram Math Open Reference. (Definition and properties.)
• Area of a Parallelogram Math Open Reference.
• Area of Parallelogram Cut The Knot.
• Equilateral Triangles On Sides of a Parallelogram Cut The Knot.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Parallelogram  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Parallelogram"

Note: Some restrictions may apply to use of individual images which are separately licensed.