Line (mathematics)

A representation of one line

A line can be described as an ideal zero-width, infinitely long, perfectly straight curve (the term curve in mathematics includes "straight curves") containing an infinite number of points. In Euclidean geometry, exactly one line can be found that passes through any two points. The line provides the shortest connection between the points.

In two dimensions, two different lines can either be parallel, meaning they never meet, or may intersect at one and only one point. In three or more dimensions, lines may also be skew, meaning they don't meet, but also don't define a plane. Two distinct planes intersect in at most one line. Three or more points that lie on the same line are called collinear.

Three lines—the red and blue lines have same slope, while the red and green ones have same y-intercept.

Examples

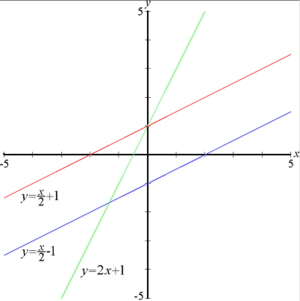
Lines in a Cartesian plane can be described algebraically by linear equations and linear functions. In two dimensions, the characteristic equation is often given by the slope-intercept form:

$y=mx+b\,$

where:

m is the slope of the line.

b is the y-intercept of the line.

x is the independent variable of the function y.

In three dimensions, a line is often described by parametric equations:

$x=x_{0}+at\,$

$y=y_{0}+bt\,$

$z=z_{0}+ct\,$

where:

x, y, and z are all functions of the independent variable t.

$x_{0}$, $y_{0}$, and $z_{0}$ are the initial values of each respective variable.

a, b, and c are related to the slope of the line, such that the vector (a, b, c) is a parallel to the line.

Formal definitions

This intuitive concept of a line can be formalized in various ways. If geometry is developed axiomatically (as in Euclid's Elements and later in David Hilbert's Foundations of Geometry), then lines are not defined at all, but characterized axiomatically by their properties. While Euclid did define a line as "length without breadth," he did not use this rather obscure definition in his later development.

In Euclidean space Rⁿ (and analogously in all other vector spaces), we define a line L as a subset of the form

$L=\{\mathbf {a} +t\mathbf {b} \mid t\in \mathbb {R} \}$

where a and b are given vectors in Rⁿ with b non-zero. The vector b describes the direction of the line, and a is a point on the line. Different choices of a and b can yield the same line.

Properties

In a two-dimensional space, such as the plane, two different lines must either be parallel lines or must intersect at one point. In higher-dimensional spaces however, two lines may do neither, and two such lines are called skew lines.

In R², every line L is described by a linear equation of the form

$L=\{(x,y)\mid ax+by=c\}\,$

with fixed real coefficients a, b and c such that a and b are not both zero (see Linear equation for other forms). Important properties of these lines are their slope, x-intercept and y-intercept. The eccentricity of a straight line is infinity.

More abstractly, one usually thinks of the real line as the prototype of a line, and assumes that the points on a line stand in a one-to-one correspondence with the real numbers. However, one could also use the hyperreal numbers for this purpose, or even the long line of topology.

The "straightness" of a line, interpreted as the property that it minimizes distances between its points, can be generalized and leads to the concept of geodesics on differentiable manifolds.

Ray

In Euclidean geometry, a ray, or half-line, given two distinct points A (the origin) and B on the ray, is the set of points C on the line containing points A and B such that A is not strictly between C and B. In geometry, a ray starts at one point, then goes on forever in one direction.

External links

All links retrieved October 29, 2022.

• Detailed explanation of the line Wolfram MathWorld
• Equations of the Straight Line Cut The Knot

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Line (mathematics)  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Line (mathematics)"

Note: Some restrictions may apply to use of individual images which are separately licensed.