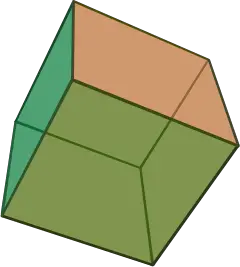
Cube

This article is about the geometric shape.

Regular Hexahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 6, E = 12 V = 8 (χ = 2)
Faces by sides	6{4}
Schläfli symbol	{4,3}
Wythoff symbol	3 | 2 4
Coxeter-Dynkin
Symmetry	Oh
References	U06, C18, W3
Properties	Regular convex zonohedron
Dihedral angle	90°
4.4.4 (Vertex figure)	Octahedron (dual polyhedron)
Net

A cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and of three-sided trapezohedron. The cube is dual to the octahedron. It has cubical symmetry (also called octahedral symmetry).

A cube is the three-dimensional case of the more general concept of a hypercube, which exists in any dimension.

Cartesian coordinates

For a cube centered at the origin, with edges parallel to the axes and with an edge length of two, the Cartesian coordinates of the vertices are

(±1,±1,±1)

while the interior consists of all points (x₀, x₁, x₂) with -1 $<$ x_i $<$ 1.

Formulas

For a cube of edge length $a$,

surface area	$6a^{2}$
volume	$a^{3}$
radius of circumscribed sphere	${\frac {{\sqrt {3}}a}{2}}$
radius of sphere tangent to edges	${\frac {a}{\sqrt {2}}}$
radius of inscribed sphere	${\frac {a}{2}}$

As the volume of a cube is the third power of its sides a×a×a, third powers are called cubes, by analogy with squares and second powers.

A cube construction has the largest volume among cuboids (rectangular boxes) with a given surface area (e.g., paper, cardboard, sheet metal, etc.). Also, a cube has the largest volume among cuboids with the same total linear size (length + width + height).

Symmetry

The cube has three classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry O_h has all the faces the same color. The dihedral symmetry D_4h comes from the cube being a prism, with all four sides being the same color. The lowest symmetry D_2h is also a prismatic symmetry, with sides alternating colors, so there are three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.

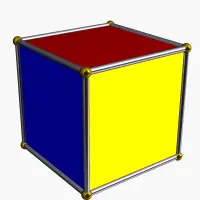(3 colors) | 2 2 2 D2h

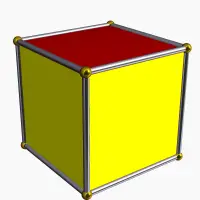(2 colors) 4 2 | 2 D4h

(1 color) 3 | 4 2 Oh

Geometric relations

The cube is unique among the Platonic solids for being able to tile space regularly. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).

Other dimensions

The familiar six-sided dice are cube shaped.

The analogue of a cube in four-dimensional Euclidean space has a special name—a tesseract or (rarely) hypercube.

The analog of the cube in n-dimensional Euclidean space is called a hypercube or n-dimensional cube or simply n-cube. It is also called a measure polytope.

In math theory you can also have lower dimensional cube. A 0th dimensional cube is simply a point. A first dimensional cube is a segment. A second dimensional cube is a square.

Related polyhedra

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron. These two together form a regular compound, the stella octangula. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other.

One such regular tetrahedron has a volume of one-third of that of the cube. The remaining space consists of four equal irregular polyhedra with a volume of one-sixth of that of the cube, each.

The rectified cube is the cuboctahedron. If smaller corners are cut off we get a polyhedron with six octagonal faces and eight triangular ones. In particular we can get regular octagons (truncated cube). The rhombicuboctahedron is obtained by cutting off both corners and edges to the correct amount.

A cube can be inscribed in a dodecahedron so that each vertex of the cube is a vertex of the dodecahedron and each edge is a diagonal of one of the dodecahedron's faces; taking all such cubes gives rise to the regular compound of five cubes.

• 

  The tetrahedra in the cube (stella octangula)

• 

  The rectified cube (cuboctahedron)

• 

  Truncated cube

• 

  Rhombicuboctahedron

The figures shown have the same symmetries as the cube (see octahedral symmetry).

Combinatorial cubes

A different kind of cube is the cube graph, which is the graph of vertices and edges of the geometrical cube. It is a special case of the hypercube graph.

An extension is the three-dimensional k-ary Hamming graph, which for k = two is the cube graph. Graphs of this sort occur in the theory of parallel processing in computers.

See also

• Polyhedron
• Square (geometry)

References

ISBN links support NWE through referral fees

• Arnone, Wendy. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley), 2001. ISBN 0764553240
• Cromwell, Peter R. Polyhedra. Cambridge, U.K.: Cambridge University Press, 1997. ISBN 0521664055
• Hartshorne, Robin. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer, 2002. ISBN 0387986502
• Leff, Lawrence S. Geometry the Easy Way. Hauppauge, NY: Barron’s Educational Series, 1997. ISBN 0764101102
• MacLean, Kenneth J.M. A Geometric Analysis of the Platonic Solids and Other Semi-Regular Polyhedra: With an Introduction to the Phi Ratio. Geometric Explorations Series. Ann Arbor, MI: Loving Healing Press, 2007. ISBN 978-1932690996
• Pearce, Peter. Structure in Nature is a Strategy for Design. Cambridge: MIT Press, 1980. ISBN 0262660458
• Smith, Joseph V. Geometrical and Structural Crystallography. Smith and Wyllie Intermediate Geology Series. New York: Wiley, 1982. ISBN 0471861685
• Stillwell, John. The Four Pillars of Geometry. Undergraduate Texts in Mathematics. New York: Springer, 2005. ISBN 0387255303
• Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. New York: Dover, 1979. ISBN 048623729X

External links

All links retrieved January 11, 2024.

• Eric W. Weisstein. Cube. MathWorld
• The Uniform Polyhedra
• Paper Models of Polyhedra

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Cube  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Cube"

Note: Some restrictions may apply to use of individual images which are separately licensed.