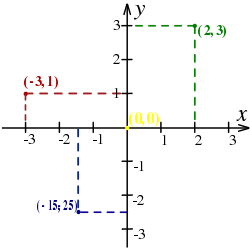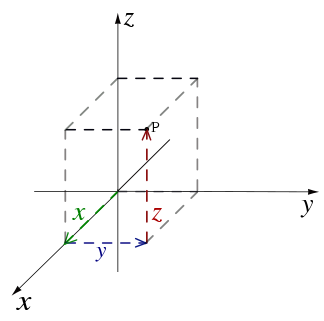Cartesian coordinate system

Fig. 1 - Cartesian coordinate system. Four points are marked: (2,3) in green, (-3,1) in red, (-1.5,-2.5) in blue and (0,0), the origin, in yellow.

In mathematics, the Cartesian coordinate system (or rectangular coordinate system) is used to determine each point uniquely in a plane through two numbers, usually called the x-coordinate and the y-coordinate of the point. To define the coordinates, two perpendicular directed lines (the x-axis or abscissa, and the y-axis or ordinate), are specified, as well as the unit length, which is marked off on the two axes (see Figure 1). Cartesian coordinate systems are also used in space (where three coordinates are used) and in higher dimensions.

Fig. 2 - Cartesian coordinate system with the circle of radius 2 centered at the origin marked in red. The equation of the circle is x² + y² = 4.

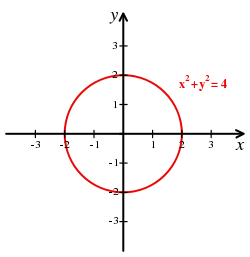
Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by algebraic equations, namely equations satisfied by the coordinates of the points lying on the shape. For example, a circle of radius 2 may be described by the equation x² + y² = 4 (see Figure 2).

History

Cartesian means relating to the French mathematician and philosopher René Descartes (Latin: Cartesius), who, among other things, worked to merge algebra and Euclidean geometry. This work was influential in the development of analytic geometry, calculus, and cartography.

The idea of this system was developed in 1637 in two writings by Descartes. In part two of his Discourse on Method, Descartes introduces the new idea of specifying the position of a point or object on a surface, using two intersecting axes as measuring guides. In La Géométrie, he further explores the above-mentioned concepts.

Two-dimensional coordinate system

Fig. 3 - The four quadrants of a Cartesian coordinate system. The arrows on the axes indicate that they extend forever in their respective directions (i.e. infinitely).

A Cartesian coordinate system in two dimensions is commonly defined by two axes, at right angles to each other, forming a plane (an xy-plane). The horizontal axis is normally labeled x, and the vertical axis is normally labeled y. In a three–dimensional coordinate system, another axis, normally labeled z, is added, providing a third dimension of space measurement. The axes are commonly defined as mutually orthogonal to each other (each at a right angle to the other). (Early systems allowed "oblique" axes, that is, axes that did not meet at right angles, and such systems are occasionally used today, although mostly as theoretical exercises.) All the points in a Cartesian coordinate system taken together form a so-called Cartesian plane. Equations that use the Cartesian coordinate system are called Cartesian equations.

The point of intersection, where the axes meet, is called the origin normally labeled O. The x and y axes define a plane that is referred to as the xy plane. Given each axis, choose a unit length, and mark off each unit along the axis, forming a grid. To specify a particular point on a two dimensional coordinate system, indicate the x unit first (abscissa), followed by the y unit (ordinate) in the form (x,y), an ordered pair.

The choice of letters comes from a convention, to use the latter part of the alphabet to indicate unknown values. In contrast, the first part of the alphabet was used to designate known values.

An example of a point P on the system is indicated in Figure 3, using the coordinate (3,5).

The intersection of the two axes creates four regions, called quadrants, indicated by the Roman numerals I (+,+), II (−,+), III (−,−), and IV (+,−). Conventionally, the quadrants are labeled counter-clockwise starting from the upper right ("northeast") quadrant. In the first quadrant, both coordinates are positive, in the second quadrant x-coordinates are negative and y-coordinates positive, in the third quadrant both coordinates are negative and in the fourth quadrant, x-coordinates are positive and y-coordinates negative (see table below.)

Three-dimensional coordinate system

Fig. 4 - Three dimensional Cartesian coordinate system with y-axis pointing away from the observer.

Fig. 5 - Three dimensional Cartesian coordinate system with the x-axis pointing towards the observer.

The three dimensional Cartesian coordinate system provides the three physical dimensions of space—length, width, and height. Figures 4 and 5, show two common ways of representing it.

The three Cartesian axes defining the system are perpendicular to each other. The relevant coordinates are of the form (x,y,z). As an example, figure 4 shows two points plotted in a three-dimensional Cartesian coordinate system: P(3,0,5) and Q(−5,−5,7). The axes are depicted in a "world-coordinates" orientation with the z-axis pointing up.

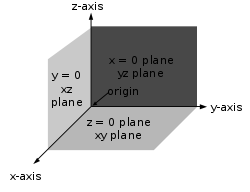
The x-, y-, and z-coordinates of a point can also be taken as the distances from the yz-plane, xz-plane, and xy-plane respectively. Figure 5 shows the distances of point P from the planes.

The xy-, yz-, and xz-planes divide the three-dimensional space into eight subdivisions known as octants, similar to the quadrants of 2D space. While conventions have been established for the labelling of the four quadrants of the x-y plane, only the first octant of three dimensional space is labelled. It contains all of the points whose x, y, and z coordinates are positive.

The z-coordinate is also called applicate.

Orientation and handedness

see also: right-hand rule

In two dimensions

The right hand rule.

Fixing or choosing the x-axis determines the y-axis up to direction. Namely, the y-axis is necessarily the perpendicular to the x-axis through the point marked 0 on the x-axis. But there is a choice of which of the two half lines on the perpendicular to designate as positive and which as negative. Each of these two choices determines a different orientation (also called handedness) of the Cartesian plane.

The usual way of orienting the axes, with the positive x-axis pointing right and the positive y-axis pointing up (and the x-axis being the "first" and the y-axis the "second" axis) is considered the positive or standard orientation, also called the right-handed orientation.

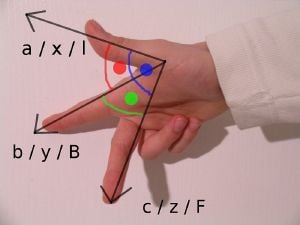
A commonly used mnemonic for defining the positive orientation is the right hand rule. Placing a somewhat closed right hand on the plane with the thumb pointing up, the fingers point from the x-axis to the y-axis, in a positively oriented coordinate system.

The other way of orienting the axes is following the left hand rule, placing the left hand on the plane with the thumb pointing up.

Regardless of the rule used to orient the axes, rotating the coordinate system will preserve the orientation. Switching the role of x and y will reverse the orientation.

In three dimensions

Fig. 7 - The left-handed orientation is shown on the left, and the right-handed on the right.

Fig. 8 - The right-handed Cartesian coordinate system indicating the coordinate planes.

Once the x- and y-axes are specified, they determine the line along which the z-axis should lie, but there are two possible directions on this line. The two possible coordinate systems which result are called "right-handed" and "left-handed." The standard orientation, where the xy-plane is horizontal and the z-axis points up (and the x- and the y-axis form a positively oriented two-dimensional coordinate system in the xy-plane if observed from above the xy-plane) is called right-handed or positive.

The name derives from the right-hand rule. If the index finger of the right hand is pointed forward, the middle finger bent inward at a right angle to it, and the thumb placed at a right angle to both, the three fingers indicate the relative directions of the x-, y-, and z-axes in a right-handed system. The thumb indicates the x-axis, the index finger the y-axis and the middle finger the z-axis. Conversely, if the same is done with the left hand, a left-handed system results.

Different disciplines use different variations of the coordinate systems. For example, mathematicians typically use a right-handed coordinate system with the y-axis pointing up, while engineers typically use a left-handed coordinate system with the z-axis pointing up. This has the potential to lead to confusion when engineers and mathematicians work on the same project.

Figure 7 is an attempt at depicting a left- and a right-handed coordinate system. Because a three-dimensional object is represented on the two-dimensional screen, distortion and ambiguity result. The axis pointing downward (and to the right) is also meant to point towards the observer, whereas the "middle" axis is meant to point away from the observer. The red circle is parallel to the horizontal xy-plane and indicates rotation from the x-axis to the y-axis (in both cases). Hence the red arrow passes in front of the z-axis.

Figure 8 is another attempt at depicting a right-handed coordinate system. Again, there is an ambiguity caused by projecting the three-dimensional coordinate system into the plane. Many observers see Figure 8 as "flipping in and out" between a convex cube and a concave "corner." This corresponds to the two possible orientations of the coordinate system. Seeing the figure as convex gives a left-handed coordinate system. Thus, the "correct" way to view Figure 8 is to imagine the x-axis as pointing towards the observer and thus seeing a concave corner.

In physics

The above discussion applies to Cartesian coordinate systems in mathematics, where it is common to not use any units of measurement. In physics, it is important to note that a dimension is simply a measure of something, and that, for each class of features to be measured, another dimension can be added. Attachment to visualizing the dimensions precludes understanding the many different dimensions that can be measured (time, mass, color, cost, etc.). Multi-dimensional objects can be calculated and manipulated algebraically.

Representing a vector with Cartesian notation

A point in space in a Cartesian coordinate system may also be represented by a vector, which can be thought of as an arrow pointing from the origin of the coordinate system to the point. If the coordinates represent spatial positions (displacements) it is common to represent the vector from the origin to the point of interest as $\mathbf {r}$. Using Cartesian coordinates, the vector from the origin to the point $(x,y,z)$ can be written as:

$\mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k}$

where $\mathbf {i}$, $\mathbf {j}$, and $\mathbf {k}$ are unit vectors that point the same direction as the $x$, $y$, and $z$ axes, respectively.

This notation is typically referred to as Cartesian notation. The unit vectors $\mathbf {i}$, $\mathbf {j}$, and $\mathbf {k}$ are called the versors of the coordinate system, and represent an example of standard basis.

Further notes

In computer geometry, the Cartesian coordinate system is the foundation for the algebraic manipulation of geometrical shapes. Many other coordinate systems have been developed since Descartes. One common set of systems uses polar coordinates; astronomers often use spherical coordinates, a type of polar coordinate system.

See also

• Curve
• Geometry
• Graph
• Line (mathematics)
• Mathematics
• Number
• Plane (mathematics)
• Point (geometry)
• René Descartes

References

ISBN links support NWE through referral fees

• Descartes, René. 2001. Discourse on Method, Optics, Geometry, and Meteorology. Trans. Paul J. Olscamp. Indianapolis, IN: Hackett Pub. ISBN 0872205673.
• Gelʹfand, I. M., E. G. Glagoleva, and A. A. Kirillov. 1990. The Method of Coordinates. Boston: Birkhauser. ISBN 0817635335.
• Kline, Morris. 1985. Mathematics for the Nonmathematician. New York: Dover. ISBN 0817635335.

External links

All links retrieved November 28, 2023.

• Cartesian Coordinate System.
• Printable Cartesian Coordinates.
• Cartesian coordinates. PlanetMath.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Cartesian coordinate system  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Cartesian coordinate system"

Note: Some restrictions may apply to use of individual images which are separately licensed.