Tide

This article is about tides in the Earth's oceans.

The Bay of Fundy at high tide

Tides are the cyclic rising and falling of the Earth's ocean surface caused by the tidal forces of the Moon and Sun acting on the oceans. Tides cause changes in the depth of the marine and estuarine water bodies and produce oscillating currents known as tidal streams, making prediction of tides important for coastal navigation (see Tides and navigation). The strip of seashore that is submerged at high tide and exposed at low tide, called the intertidal zone, is an important ecological product of ocean tides (see Intertidal ecology).

The Bay of Fundy at low tide

The changing tide produced at a given location is the result of several factors, including the changing positions of the Moon and Sun relative to the Earth, the effects of Earth's rotation, and local water depth. Sea level measured by coastal tide gauges may also be strongly affected by wind. More generally, tidal phenomena can occur in other systems besides the ocean, whenever a gravitational field that varies in time and space is present (see Other tides).

Introduction and tidal terminology

A tide is a repeated cycle of sea level changes in the following stages:

• Over several hours the water rises or advances up a beach in the flood tide.
• The water reaches its highest level and stops at high tide. Because tidal currents cease this is also called slack water or slack tide. The tide reverses direction and is said to be turning.
• The sea level recedes or falls over several hours during the ebb tide.
• The level stops falling at low tide. This point is also described as slack or turning.

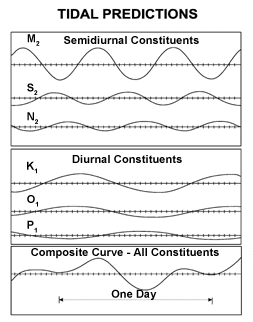
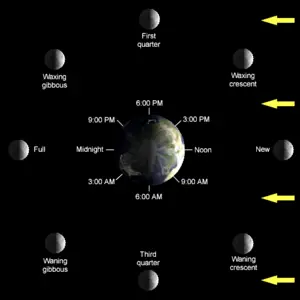
Tides may be semidiurnal (two high tides and two low tides each day), or diurnal (one tidal cycle per day). In most locations, tides are semidiurnal. Because of the diurnal contribution, there is a difference in height (the daily inequality) between the two high tides on a given day; these are differentiated as the higher high water and the lower high water in tide tables. Similarly, the two low tides each day are referred to as the higher low water and the lower low water. The daily inequality changes with time and is generally small when the Moon is over the equator.

The various frequencies of astronomical forcing which contribute to tidal variations are called constituents. In most locations, the largest is the "principal lunar semidiurnal" constituent, also known as the M2 (or M₂) tidal constituent. Its period is about 12 hours and 24 minutes, exactly half a tidal lunar day, the average time separating one lunar zenith from the next, and thus the time required for the Earth to rotate once relative to the Moon. This is the constituent tracked by simple tide clocks.

Tides vary on timescales ranging from hours to years, so to make accurate records tide gauges measure the water level over time at fixed stations which are screened from variations caused by waves shorter than minutes in period. This data is compared to the reference (or datum) level usually called mean sea level.

Constituents other than M₂ arise from factors such as the gravitational influence of the Sun, the tilt of the Earth's rotation axis, the inclination of the lunar orbit and the ellipticity of the orbits of the Moon about the Earth and the Earth about the Sun. Variations with periods of less than half a day are called harmonic constituents. Long period constituents have periods of days, months, or years.

Tidal range variation: springs and neaps

An artist's conception of spring tide

An artist's conception of neap tide

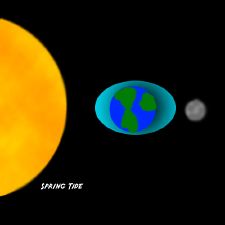
The semidiurnal tidal range (the difference in height between high and low tides over about a half day) varies in a two-week or fortnightly cycle. Around new and full moon when the Sun, Moon and Earth form a line (a condition known as syzygy), the tidal forces due to the Sun reinforce those of the Moon. The tide's range is then maximum: this is called the spring tide, or just springs and is derived not from the season of spring but rather from the verb meaning "to jump" or "to leap up." When the Moon is at first quarter or third quarter, the Sun and Moon are separated by 90° when viewed from the earth, and the forces due to the Sun partially cancel those of the Moon. At these points in the lunar cycle, the tide's range is minimum: this is called the neap tide, or neaps. Spring tides result in high waters that are higher than average, low waters that are lower than average, slack water time that is shorter than average and stronger tidal currents than average. Neaps result in less extreme tidal conditions. There is about a seven day interval between springs and neaps.

The changing distance of the Moon from the Earth also affects tide heights. When the Moon is at perigee the range is increased and when it is at apogee the range is reduced. Every 7½ lunations, perigee and (alternately) either a new or full moon coincide causing perigean tides with the largest tidal range, and if a storm happens to be moving onshore at this time, the consequences (in the form of property damage, etc.) can be especially severe.

Tidal phase and amplitude

The M₂ tidal constituent. Amplitude is indicated by color, and the white lines are cotidal differing by 1 hr. The curved arcs around the amphidromic points show the direction of the tides, each indicating a synchronized 6 hour period.

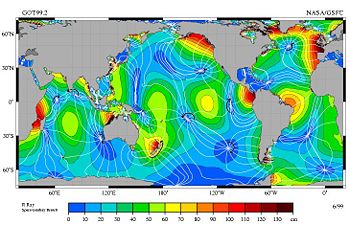
Because the M₂ tidal constituent dominates in most locations, the stage or phase of a tide, denoted by the time in hours after high tide, is a useful concept. It is also measured in degrees, with 360° per tidal cycle. Lines of constant tidal phase are called cotidal lines. High tide is reached simultaneously along the cotidal lines extending from the coast out into the ocean, and cotidal lines (and hence tidal phases) advance along the coast.

If one thinks of the ocean as a circular basin enclosed by a coastline, the cotidal lines point radially inward and must eventually meet at a common point, the amphidromic point. An amphidromic point is at once cotidal with high and low tides, which is satisfied by zero tidal motion. (The rare exception occurs when the tide circles around an island, as it does around New Zealand.) Indeed tidal motion generally lessens moving away from the continental coasts, so that crossing the cotidal lines are contours of constant amplitude (half of the distance between high and low tide) which decrease to zero at the amphidromic point. For a 12 hour semidiurnal tide the amphidromic point behaves roughly like a clock face, with the hour hand pointing in the direction of the high tide cotidal line, which is directly opposite the low tide cotidal line. High tide rotates about once every 12 hours in the direction of rising cotidal lines, and away from ebbing cotidal lines. The difference of cotidal phase from the phase of a reference tide is the epoch.

The shape of the shoreline and the ocean floor change the way that tides propagate, so there is no simple, general rule for predicting the time of high tide from the position of the Moon in the sky. Coastal characteristics such as underwater topography and coastline shape mean that individual location characteristics need to be taken into consideration when forecasting tides; high water time may differ from that suggested by a model such as the one above due to the effects of coastal morphology on tidal flow.

Tidal physics

The Earth and Moon, looking at the North Pole

Isaac Newton laid the foundations for the mathematical explanation of tides in the Philosophiae Naturalis Principia Mathematica (1687). In 1740, the Académie Royale des Sciences in Paris offered a prize for the best theoretical essay on tides. Daniel Bernoulli, Antoine Cavalleri, Leonhard Euler, and Colin Maclaurin shared the prize. Maclaurin used Newton’s theory to show that a smooth sphere covered by a sufficiently deep ocean under the tidal force of a single deforming body is a prolate spheroid with major axis directed toward the deforming body. Maclaurin was also the first to write about the Earth's rotational effects on motion. Euler realized that the horizontal component of the tidal force (more than the vertical) drives the tide. In 1744 D'Alembert studied tidal equations for the atmosphere which did not include rotation. The first major theoretical formulation for water tides was made by Pierre-Simon Laplace, who formulated a system of partial differential equations relating the horizontal flow to the surface height of the ocean. The Laplace tidal equations are still in use today. William Thomson rewrote Laplace's equations in terms of vorticity which allowed for solutions describing tidally driven coastally trapped waves, which are known as Kelvin waves.

Tidal forces

A schematic of the Earth-Moon system, showing the entire Earth following the motion of its center of gravity.

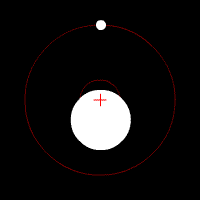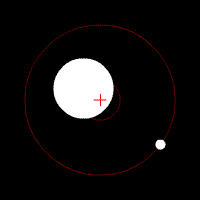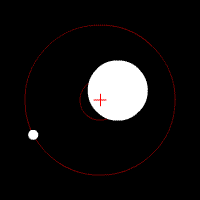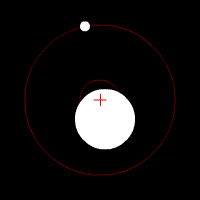
The tidal force produced by a massive object (Moon, hereafter) on a small particle located on or in an extensive body (Earth, hereafter) is the vector difference between the gravitational force exerted by the Moon on the particle, and the gravitational force that would be exerted on the particle if it were located at the center of mass of the Earth. Thus, the tidal force depends not on the strength of the gravitational field of the Moon, but on its gradient.

The gravitational force exerted on the Earth by the Sun is on average 179 times stronger than that exerted on the Earth by the Moon, but because the Sun is on average 389 times farther from the Earth, the gradient of its field is weaker. The tidal force produced by the Sun is therefore only 46% as large as that produced by the Moon.

Tidal forces can also be analyzed from the point of view of a reference frame that translates with the center of mass of the Earth. Consider the tide due to the Moon (the Sun is similar). First observe that the Earth and Moon rotate around a common orbital center of mass, as determined by their relative masses. The orbital center of mass is 3/4 of the way from the Earth's center to its surface. The second observation is that the Earth's centripetal motion is the averaged response of the entire Earth to the Moon's gravity and is exactly the correct motion to balance the Moon's gravity only at the center of the Earth; but every part of the Earth moves along with the center of mass and all parts have the same centripetal motion, since the Earth is rigid.

On the other hand each point of the Earth experiences the Moon's radially decreasing gravity differently; the near parts of the Earth are more strongly attracted than is compensated by the centripetal motion and experience a net tidal force toward the Moon; the far parts have more centripetal motion than is necessary for the reduced attraction, and thus feel a net force away from the Moon.

Finally only the horizontal components of the tidal forces actually contribute tidal acceleration to the water particles since there is small resistance. The actual tidal force on a particle is only about a ten millionth of the force caused by the Earth's gravity.

The Moon's (or Sun's) gravity differential field at the surface of the earth is known as the tide generating force. This is the primary mechanism that drives tidal action and explains two tidal equipotential bulges, accounting for two high tides per day.

The ocean's surface is closely approximated by an equipotential surface, (ignoring ocean currents) which is commonly referred to as the geoid. Since the gravitational force is equal to the gradient of the potential, there are no tangential forces on such a surface, and the ocean surface is thus in gravitational equilibrium.

Now consider the effect of external, massive bodies such as the Moon and Sun. These bodies have strong gravitational fields that diminish with distance in space and which act to alter the shape of an equipotential surface on the Earth. Gravitational forces follow an inverse-square law (force is inversely proportional to the square of the distance), but tidal forces are inversely proportional to the cube of the distance. The ocean surface moves to adjust to changing tidal equipotential, tending to rise when the tidal potential is high, the part of the Earth nearest the Moon, and the farthest part. When the tidal equipotential changes, the ocean surface is no longer aligned with it, so that the apparent direction of the vertical shifts. The surface then experiences a down slope, in the direction that the equipotential has risen.

Laplace tidal equation

The depth of the oceans is much smaller than their horizontal extent; thus, the response to tidal forcing can be modeled using the Laplace tidal equations which incorporate the following features: (1) the vertical (or radial) velocity is negligible, and there is no vertical shear—this is a sheet flow. (2) The forcing is only horizontal (tangential). (3) the Coriolis effect appears as a fictitious lateral forcing proportional to velocity. (4) the rate of change of the surface height is proportional to the negative divergence of velocity multiplied by the depth. The last means that as the horizontal velocity stretches or compresses the ocean as a sheet, the volume thins or thickens, respectively.

The boundary conditions dictate no flow across the coastline, and free slip at the bottom. The Coriolis effect steers waves to the right in the northern hemisphere and to the left in the southern allowing coastally trapped waves. Finally, a dissipation term can be added which is an analog to viscosity.

Tidal amplitude and cycle time

The theoretical amplitude of oceanic tides due to the Moon is about 54 cm at the highest point, which corresponds to the amplitude that would be reached if the ocean possessed a uniform depth, there were no landmasses, and the Earth were not rotating. The Sun similarly causes tides, of which the theoretical amplitude is about 25 cm (46% of that of the Moon) with a cycle time of 12 hours. At spring tide the two effects add to each other to a theoretical level of 79 cm, while at neap tide the theoretical level is reduced to 29 cm. Since the orbits of the Earth about the Sun, and the Moon about the Earth, are elliptical, the amplitudes of the tides change somewhat as a result of the varying Earth-Sun and Earth-Moon distances. This causes a variation in the tidal force and theoretical amplitude of about ±18 percent for the Moon and ±5 percent for the Sun. If both the Sun and Moon were at their closest positions and aligned at new moon, the theoretical amplitude would reach 93 cm.

Real amplitudes differ considerably, not only because of variations in ocean depth, and the obstacles to flow caused by the continents, but also because the natural period of wave propagation is of the same order of magnitude as the rotation period: about 30 hours. If there were no land masses, it would take about 30 hours for a long wavelength ocean surface wave to propagate along the equator halfway around the Earth (by comparison, the natural period of the Earth's lithosphere is about 57 minutes).

Tidal dissipation

The tidal forcing is essentially driven by orbital energy of the Earth Moon system at a rate of about 3.75 Terawatts. The dissipation arises as the basin scale tidal flow drives smaller scale flows which experience turbulent dissipation. This tidal drag gives rise to a torque on the Moon that results in the gradual transfer of angular momentum to its orbit, and a gradual increase in the Earth-Moon separation. As a result of the principle of conservation of angular momentum, the rotational velocity of the Earth is correspondingly slowed. Thus, over geologic time, the Moon recedes from the Earth, at about 3.8 cm/year, and the length of the terrestrial day increases, meaning that there is about 1 less day per 100 million years.

Tidal observation and prediction

From ancient times, tides have been observed and discussed with increasing sophistication, first noting the daily recurrence, then its relationship to the Sun and Moon. Eventually the first tide table in China was recorded in 1056 C.E. primarily for the benefit of visitors to see the famous tidal bore in the Qiantang River. In Europe the first known tide-table is thought to be that of John, Abbott of Wallingford (d. 1213), based on high water occurring 48 minutes later each day, and three hours later at London than at the mouth of the Thames. William Thomson led the first systematic harmonic analysis to tidal records starting in 1867. The main result was the building of a tide-predicting machine (TPM) on using a system of pulleys to add together six harmonic functions of time. It was "programmed" by resetting gears and chains to adjust phasing and amplitudes. Similar machines were used until the 1960s.

The first known sea-level record of an entire spring–neap cycle was made in 1831 on the Navy Dock in the Thames Estuary, and many large ports had automatic tide gages stations by 1850.

William Whewell first mapped co-tidal lines ending with a nearly global chart in 1836. In order to make these maps consistent, he hypothesized the existence of amphidromes where co-tidal lines meet in the mid-ocean. These points of no tide were confirmed by measurement in 1840 by Captain Hewett, RN, from careful soundings in the North Sea.

Timing

The same tidal forcing has different results depending on many factors, including coast orientation, continental shelf margin, water body dimensions.

In most places there is a delay between the phases of the Moon and the effect on the tide. Springs and neaps in the North Sea, for example, are two days behind the new/full Moon and first/third quarter. This is called the age of the tide.

The exact time and height of the tide at a particular coastal point is also greatly influenced by the local bathymetry. There are some extreme cases: the Bay of Fundy, on the east coast of Canada, features the largest well-documented tidal ranges in the world, 16 meters (53 ft), because of the shape of the bay . Southampton in the United Kingdom has a double high tide caused by the interaction between the different tidal harmonics within the region. This is contrary to the popular belief that the flow of water around the Isle of Wight creates two high waters. The Isle of Wight is important, however, as it is responsible for the 'Young Flood Stand', which describes the pause of the incoming tide about three hours after low water.

There are only very slight tides in the Mediterranean Sea and the Baltic Sea owing to their narrow connections with the Atlantic Ocean. Extremely small tides also occur for the same reason in the Gulf of Mexico and Sea of Japan. On the southern coast of Australia, because the coast is extremely straight (partly due to the tiny quantities of runoff flowing from rivers), tidal ranges are equally small.

Tidal analysis

Tidal prediction summing constituent.

Careful Fourier and data analysis over a 19 year period (the National Tidal Datum Epoch in the US) uses carefully selected frequencies called the tidal harmonic constituents. This analysis can be done using only the knowledge of the period of forcing, but without detailed understanding of the physical mathematics, which means that useful tidal tables have been constructed for centuries.

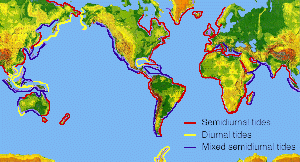
The resulting amplitudes and phases can then be used to predict the expected tides. These are usually dominated by the constituents near 12 hours (the semidiurnal constituents), but there are major constituents near 24 hours (diurnal) as well. Longer term constituents are 14 day or fortnightly, monthly, and semiannual. Most coastline is dominated by semidiurnal tides, but some areas such as the South China Sea and the Gulf of Mexico are primarily diurnal. In the semidiurnal areas, the primary constituents M₂(lunar) and S₂(solar) periods differ slightly so that the relative phases, and thus the amplitude of the combined tide, change fortnightly (14 day period).

In the M₂ plot above each cotidal line differs by 1 hour from its neighbors, and the thicker lines show tides in phase with equilibrium at Greenwich. The lines rotate around the amphidromic points counterclockwise in the northern hemisphere so that from Baja California to Alaska and from France to Ireland the M₂ tide propagates northward. In the southern hemisphere this direction is clockwise. On the other hand M₂ tide propagates counterclockwise around New Zealand, but this because the islands act as dam and permit the tides to have different heights on opposite sides of the islands. But the tides do propagate northward on the eastside and southward on the west coast, as predicted by theory.

The exception is the Cook Strait where the tidal currents periodically link high to low tide. This is because cotidal lines 180° around the amphidromes are in opposite phase, for example high tide across from low tide. Each tidal constituent has a different pattern of amplitudes, phases, and amphidromic points, so the M₂ patterns cannot be used for other tides.

Tides and navigation

Hall's Harbour Low and High Tide

Tidal flows are of profound importance in navigation and very significant errors in position will occur if they are not taken into account. Tidal heights are also very important; for example many rivers and harbors have a shallow "bar" at the entrance which will prevent boats with significant draft from entering at certain states of the tide.

The timings and velocities of tidal flow can be found by looking at a tidal chart or tidal stream atlas for the area of interest. Tidal charts come in sets, with each diagram of the set covering a single hour between one high tide and another (they ignore the extra 24 minutes) and give the average tidal flow for that one hour. An arrow on the tidal chart indicates the direction and the average flow speed (usually in knots) for spring and neap tides. If a tidal chart is not available, most nautical charts have "tidal diamonds" which relate specific points on the chart to a table of data giving direction and speed of tidal flow.

Standard procedure to counteract the effects of tides on navigation is to (1) calculate a "dead reckoning" position (or DR) from distance and direction of travel, (2) mark this on the chart (with a vertical cross like a plus sign) and (3) draw a line from the DR in the direction of the tide. The distance the tide will have moved the boat along this line is computed by the tidal speed, and this gives an "estimated position" or EP (traditionally marked with a dot in a triangle).

Civil and maritime uses of tidal data

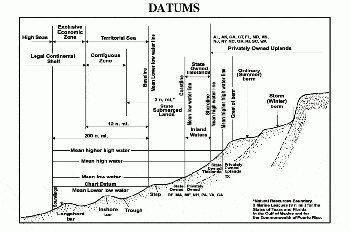
Nautical charts display the "charted depth" of the water at specific locations with "soundings" and the use of bathymetric contour lines to depict the shape of the submerged surface. These depths are relative to a "chart datum," which is typically the level of water at the lowest possible astronomical tide (tides may be lower or higher for meteorological reasons) and are therefore the minimum water depth possible during the tidal cycle. "Drying heights" may also be shown on the chart, which are the heights of the exposed seabed at the lowest astronomical tide.

Heights and times of low and high tide on each day are published in tide tables. The actual depth of water at the given points at high or low water can easily be calculated by adding the charted depth to the published height of the tide. The water depth for times other than high or low water can be derived from tidal curves published for major ports. If an accurate curve is not available, the rule of twelfths can be used. This approximation works on the basis that the increase in depth in the six hours between low and high tide will follow this simple rule: first hour - 1/12, second - 2/12, third - 3/12, fourth - 3/12, fifth - 2/12, sixth - 1/12.

Biological aspects

Intertidal ecology

A rock, seen at low tide, exhibiting typical intertidal zonation.

Intertidal ecology is the study of intertidal ecosystems, where organisms live between the low and high tide lines. At low tide, the intertidal is exposed (or ‘emersed’) whereas at high tide, the intertidal is underwater (or ‘immersed’). Intertidal ecologists therefore study the interactions between intertidal organisms and their environment, as well as between different species of intertidal organisms within a particular intertidal community. The most important environmental and species interactions may vary based on the type of intertidal community being studied, the broadest of classifications being based on substrates - rocky shore and soft bottom communities.

Organisms living in this zone have a highly variable and often hostile environment, and have evolved various adaptations to cope with, and even exploit, these conditions. One easily visible feature of intertidal communities is vertical zonation, where the community is divided into distinct vertical bands of specific species going up the shore. Species ability to cope with desiccation determines their upper limits, while competition with other species sets their lower limits.

Intertidal regions are utilized by humans for food and recreation, but anthropogenic actions also have major impacts, with overexploitation, invasive species and climate change being among the problems faced by intertidal communities. In some places Marine Protected Areas have been established to protect these areas and aid in scientific research.

Biological rhythms and the tides

Intertidal organisms are greatly affected by the approximately fortnightly cycle of the tides, and hence their biological rhythms tend to occur in rough multiples of this period. This is seen not only in the intertidal organisms however, but also in many other terrestrial animals, such as the vertebrates. Examples include gestation and the hatching of eggs. In humans, for example, the menstrual cycle lasts roughly a month, an even multiple of the period of the tidal cycle. This may be evidence of the common descent of all animals from a marine ancestor.

Other tides

In addition to oceanic tides, there are atmospheric tides as well as earth tides. All of these are continuum mechanical phenomena, the first two being fluids and the third solid (with various modifications).

Atmospheric tides are negligible from ground level and aviation altitudes, drowned by the much more important effects of weather. Atmospheric tides are both gravitational and thermal in origin, and are the dominant dynamics from about 80 km to 120 km where the molecular density becomes too small to behave as a fluid.

Earth tides or terrestrial tides that affect the entire rocky mass of the Earth. The Earth's crust shifts (up/down, east/west, north/south) in response to the Moon's and Sun's gravitation, ocean tides, and atmospheric loading.

While negligible for most human activities, the semidiurnal amplitude of terrestrial tides can reach about 55 cm at the equator (15 cm is due to the Sun) which is important in GPS calibration and VLBI measurements. Also to make precise astronomical angular measurements requires knowledge of the earth's rate of rotation and nutation, both of which are influenced by earth tides. The semi-diurnal M₂ Earth tides are nearly in phase with the Moon with tidal lag of about two hours.

Terrestrial tides also need to be taken in account in the case of some particle physics experiments. For instance, at the CERN or SLAC, the very large particle accelerators were designed while taking terrestrial tides into account for proper operation. Among the effects that need to be taken into account are for circular accelerators and particle beam energy

Since tidal forces generate currents of conducting fluids within the interior of the Earth, they affect in turn the Earth's magnetic field itself.

The galactic tide is the tidal force exerted by galaxies on stars within them and satellite galaxies orbiting them. The effects of the galactic tide on the Solar System's Oort cloud are believed to be the cause of 90 percent of all observed long-period comets.

When oscillating tidal currents in the stratified ocean flow over uneven bottom topography, they generate internal waves with tidal frequencies. Such waves are called internal tides.

Misnomers

Tsunamis, the large waves that occur after earthquakes, are sometimes called tidal waves, but this name is due to their resemblance to the tide, rather than any actual link to the tide itself. Other phenomena unrelated to tides but using the word tide are rip tide, storm tide, hurricane tide, and black tide, referring to oil spills; or red tides, that refer to algae blooms.

References

ISBN links support NWE through referral fees

• Accad, Y., and C.L. Pekeris. Solution of the Tidal Equations for the M2 and S2 Tides in the World Oceans from a Knowledge of the Tidal Potential Alone. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 290(1368) (1978): 235-266.
• Anthoni, J. Floor. Oceanography: tides Seafriends.org, 2000. Retrieved March 15, 2020.
• Cartwright, David E. Tides: A Scientific History. Cambridge, UK: Cambridge University Press, 1999. ISBN 0521797462
• Darwin, Charles. The Descent of Man, and Selection in Relation to Sex. London, UK: John Murray. Facsimile Reprint: Adamant Media Corporation, 2000. ISBN 1402184352
• Mccully, James Greig. Beyond the Moon: A Conversational, Common Sense Guide to Understanding the Tides. Singapore: World Scientific Publishing Company, 2006. ISBN 9812566449
• Open University. Waves, Tides and Shallow-Water Processes. Burlington, MA: Butterworth-Heinemann, 2000. ISBN 0750642815

External links

All links retrieved April 30, 2023.

• Our Restless Tides: NOAA's practical & short introduction to tides.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Tide  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Tide"

Note: Some restrictions may apply to use of individual images which are separately licensed.