Leonhard Euler

Leonhard Euler
Portrait by Johann Georg Brucker
Born	April 15, 1707 Basel, Switzerland
Died	September 18 [O.S. September 7] 1783 Saint Petersburg, Russia
Residence	Prussia Russia Switzerland
Nationality	Swiss
Field	Mathematics and physics
Institutions	Imperial Russian Academy of Sciences Berlin Academy
Alma mater	University of Basel
Religious stance	Lutheran

Leonhard Euler (pronounced Oiler) (April 15, 1707 – September 18, 1783) was a prolific Swiss mathematician and physicist who applied his expertise to problems in astronomy, optics, mechanical engineering, and mechanics. He introduced some of the familiar notation still used in mathematics today, and expanded the reach of the infinitesimal calculus by introducing a great number of mathematical innovations. As a religious Christian, he was deeply interested in theology. He was also a family man and at his death was survived by 26 grandchildren.

Biography

Childhood

Swiss 10 Franc banknote honoring Euler, the most successful Swiss mathematician in history.

Euler was born in Basel to Paul Euler, a pastor of the Reformed Church, and Marguerite Brucker, a pastor's daughter. The tradition of a religious life would be passed on to Euler, who remained a devout Calvinist for his entire life. Euler had two younger sisters named Anna Maria and Maria Magdalena. Soon after the birth of Leonhard, the Eulers moved from Basel to the town of Riehen, where Euler spent most of his childhood. Paul Euler was a family friend of the Bernoullis, and Johann Bernoulli, who was then regarded as Europe's foremost mathematician, would eventually be an important influence on the young Leonhard. His early formal education started in Basel, where he was sent to live with his maternal grandmother. At the age of 13 he matriculated from the University of Basel, and in 1723, at the age of 17, he received the degree of Masters of Arts with a dissertation that compared the philosophies of Descartes and Newton. At this time, he was receiving Saturday afternoon lessons from Johann Bernoulli, who quickly discovered his new pupil's incredible talent for mathematics.

Euler was at this point studying theology, Greek, and Hebrew at his father's urging, in order to become a pastor. Johann Bernoulli intervened, and convinced Paul Euler that Leonhard was destined to become a great mathematician. In 1726, Euler completed his Ph.D. dissertation on the propagation of sound with the title De Sono and in 1727, he entered the Paris Academy Prize Problem competition, where the problem that year was to find the best way to place the masts on a ship. He won second place, losing only to Pierre Bouguer—a man now known as "the father of naval architecture." Euler, however, would eventually win the coveted annual prize 12 times in his career.

Saint Petersburg

Around this time Johann Bernoulli's two sons, Daniel and Nicolaus II, were working at the Imperial Russian Academy of Sciences in Saint Petersburg. In July 1726, Nicolas died of appendicitis after spending a year in Russia, and when Daniel assumed his brother's position in the mathematics/physics division, he recommended that the post in physiology that he had vacated be filled by his friend Euler. In November 1726 Euler eagerly accepted the offer, but delayed making the trip to Saint Petersburg. In the interim he attended lectures on medicine in preparation for the post he would receive at his new assignment. At the same time, he unsuccessfully applied for a physics professorship at the University of Basel.

1957 stamp of the former Soviet Union commemorating the 250th birthday of Euler. The Text says: 250 Years from the birth of the great Mathematician and Academic, Leonhard Euler.

Euler finally arrived in the Russian capital on May 17, 1727.

The Academy at Saint Petersburg, established by Peter the Great, was intended to improve education in Russia and to close the scientific gap with Western Europe. As a result, it was made especially attractive to foreign scholars like Euler: the academy possessed ample financial resources and a comprehensive library drawn from the private libraries of Peter himself and of the nobility. Very few students were enrolled in the academy so as to lessen the faculty's teaching burden, and the academy emphasized research and offered to its faculty both the time and the freedom to pursue scientific questions.

However, the Academy's benefactress, German-born Catherine I, who had attempted to continue the progressive policies of her late husband, died the day of Euler's arrival. The Russian nobility then gained power upon the ascension of the 12-year-old Peter II. The nobility were suspicious of the academy's foreign scientists, and thus cut funding and caused numerous other difficulties for Euler and his colleagues.

Euler managed to secure a job as a medic in the Russian Navy, and contemplated making his service into a career, as he had been promised a lieutenancy and rapid promotion.

Fortunately, conditions improved slightly upon the death of Peter II, and Euler swiftly rose through the ranks in the academy and was made professor of physics in 1730. Two years later, Daniel Bernoulli, who was fed up with the censorship and hostility he faced at St. Petersburg, left for Basel. Euler succeeded him as the head of the mathematics department.

On January 7, 1734, Euler married Katharina Gsell, daughter of a painter from the Academy Gymnasium. The young couple bought a house by the Neva River, and had 13 children, of whom only five survived childhood.

In 1735, a problem was proposed for solution to members of the St. Petersburg Academy, and Euler, tackling it with all the reserves of his energy and skill, managed to solve it. But his exertions left him so fatigued that he developed a fever, and lost his sight in one eye.

The French Academy of Sciences awarded Euler a prize in 1738 for his memoir, On the Nature and the Properties of fire. In 1840, the academy awarded him a second prize, conjointly with Bernoulli and Colin Maclaurin, for work on tides.

Berlin

Concerned about continuing turmoil in Russia, Euler debated whether to stay in St. Petersburg or not. Frederick the Great of Prussia offered him a post at the Berlin Academy, which he accepted. He left St. Petersburg on June 19, 1741 and lived twenty-five years in Berlin, where he wrote over 380 articles, including some for submission to the Academy of St. Petersburg, which granted Euler a pension in 1742. In 1744, after his arrival at the court of Frederick in Berlin, he was appointed director of the mathematical class at the Prussian Academy of Science, and in the same year was awarded a prize by the academy in Paris for his work on magnetism. In 1847, he published a memoir on light dispersion, the contents of which was later applied to the improvement of telescopes. The following year, he published the Introductio in analysis infinitorum, a text on functions. He also completed the Institutiones calculi differentialis, a work on differential calculus.

In addition, Euler was asked to tutor the Princess of Anhalt-Dessau, Frederick's niece. He wrote over 200 letters to her, which were later compiled into a best-selling volume, titled the Letters of Euler on different Subjects in Natural Philosophy Addressed to a German Princess. This work contained Euler's exposition on various subjects pertaining to physics and mathematics, as well as offering valuable insight on Euler's personality and religious beliefs. This book ended up being more widely read than any of his mathematical works, and was published all across Europe and in the United States. The popularity of the Letters testifies to Euler's ability to communicate scientific matters effectively to a lay audience, a rare ability for a dedicated research scientist.

In 1750, Euler brought his elderly mother from Frankfort to his home in Berlin, where he cared for her until her death in 1761.

Around 1751, Euler was involved in a controversy surrounding the discovery of the principle of least action. The principle, in basic terms, states that bodies follow the path in which the expenditure of a physical quantity, called "action," is the least. This was an important insight, which laid the cornerstone for future developments in the theory of moving bodies (dynamics). Euler gave credit for the discovery to the president of the Prussian Academy, Pierre de Maupertuis. But another scientist and member of the Prussian Academy, Samuel Konig, claimed it had been discovered by Gottfried Wilhelm Leibnitz. This controversy caused a stir, was not well handled, and resulted in even Euler losing his customary composure, as he was strongly in support of Maupertuis's claim to the discovery.

Euler had gained such a solid international reputation that the French Academy created a ninth slot for foreign membership, and elected Euler to that position in 1755. And in 1860, when the Russian army unknowingly pillaged Euler's farm, both the army and Empress Elizabeth paid Euler a large sum in compensation, a gesture that endeared the Russian monarchy to him.

Despite Euler's immense contribution to the Academy's prestige, he was eventually forced to leave Berlin. This was caused in part by a personality conflict with Frederick. Frederick came to regard him as unsophisticated especially in comparison to the circle of philosophers the German king brought to the Academy. Voltaire was among those in Frederick's employ, and the Frenchman enjoyed a favored position in the king's social circle. Euler, a simple religious man and a hard worker, was very conventional in his beliefs and tastes. He was in many ways the direct opposite of Voltaire. Euler had very limited training in rhetoric and tended to debate matters that he knew little about, making him a frequent target of Voltaire's wit. Frederick also expressed disappointment with Euler's practical engineering abilities:

I wanted to have a water jet in my garden: Euler calculated the force of the wheels necessary to raise the water to a reservoir, from where it should fall back through channels, finally spurting out in Sanssouci. My mill was carried out geometrically and could not raise a mouthful of water closer than fifty paces to the reservoir. Vanity of vanities! Vanity of geometry!

A 1753 portrait by Emanuel Handmann. This portrayal suggests problems of the right eyelid and that Euler is perhaps suffering from strabismus. The left eye appears healthy, as it was a later cataract that destroyed it.

Last stage of life

The situation in Russia had improved greatly since the ascension of Catherine the Great, and in 1766 Euler accepted an invitation to return to the Saint Petersburg Academy. Soon after his arrival, however, Euler developed a cataract in his good left eye, rendering him almost totally blind a few weeks after its discovery. It was during this time that Euler wrote Elements of Algebra, dictating it to one of his servants, a tailor's apprentice with no formal mathematical training. Euler's condition appeared to have little effect on his productivity, as he compensated for it with his mental calculation skills and photographic memory. Euler could repeat the Aeneid of Virgil from beginning to end without hesitation, and for every page in the edition he could indicate which line was the first and which the last.

Besides his loss of eyesight, Euler was beset by other problems. A 1771 fire in St. Petersburg cost him his home and library, and almost his life. And in 1773, he lost his wife of 40 years. Euler would remarry three years later. These adversities did not prevent Euler from gaining new honors and winning more awards. With the assistance of one of his sons, he won two prizes (1770, 1772) administered by the French Academy of Sciences for papers that more clearly accounted for the movements of the moon. He also published a large work on the construction and management of seagoing vessels.

Euler's sight was restored temporarily with the help of a surgical procedure, but, perhaps because he would not wait until the effects of the surgery were healed, he lost his sight again.

Euler married again in 1776, to a woman who was the aunt of his first wife.

Euler's grave at the Alexander Nevsky Monastery.

On September 18, 1783, Euler dined with a relative, and discussed the computation of the orbit of a newly identified planet, Uranus. He then took some time to play with one of his many grandchildren, when he suffered a brain hemorrhage that took his life. He was buried at the Alexander Nevsky Lavra (Alexander Nevsky Monastery).

Euler was survived by his second wife and 26 grandchildren. His eulogy was written for the French Academy by the French mathematician and philosopher Marquis de Condorcet, and an account of his life, with a list of his works, by Nikolaus von Fuss, Euler's son-in-law and the secretary of the Imperial Academy of St. Petersburg. Condorcet commented,

"…il cessa de calculer et de vivre," (he ceased to calculate and to live).

Contributions to mathematics

Euler worked in almost all areas of mathematics: geometry, calculus, trigonometry, algebra, and number theory, not to mention continuum physics, lunar theory and other areas of physics. His importance in the history of mathematics cannot be overstated: if printed, his works, many of which are of fundamental interest, would occupy between 60 and 80 quarto volumes and Euler's name is associated with an impressive number of topics.

Mathematical notation

Euler introduced and popularized several notational conventions through his numerous and widely circulated textbooks. Most notably, he introduced the concept of a function and was the first to write f (x) to denote the function f applied to the argument x. He also introduced the modern notation for the trigonometric functions, the letter e for the base of the natural logarithm (now also known as Euler's number), the Greek letter $\Sigma$ for summations and the letter i to denote the imaginary unit. (The symbol "i" represents the mathematical entity which when multiplied by itself yields "-1".) The use of the Greek letter π to denote the ratio of a circle's circumference to its diameter was also popularized by Euler, although it did not originate with him. Euler also contributed to the development of the the history of complex numbers system (the notation system of defining negative roots with a + bi). Euler is also often credited with using the notation cos A and sin A for "cosine of A" and "sine of A" respectively. If he did not invent this notation, he was certainly one of its earliest users.

Analysis

The development of calculus was at the forefront of eighteenth-century mathematical research, and the Bernoullis—family friends of Euler—were responsible for much of the early progress in the field. Thanks to their influence, studying calculus naturally became the major focus of Euler's work. While some of Euler's proofs may not have been acceptable under modern standards of rigour, his ideas led to many great advances.

He is well known in analysis for his frequent use and development of power series: that is, the expression of functions as sums of infinitely many terms, such as

$e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=\lim _{n\to \infty }\left({\frac {1}{0!}}+{\frac {x}{1!}}+{\frac {x^{2}}{2!}}+\cdots +{\frac {x^{n}}{n!}}\right)$

In the above formula, Euler abbreviated the expression "the limit as n approches infinity," meaning that as the number of terms of the sum increases, the sum approaches one distinct value, which he called the limit, rather than becoming unmanageably large. Notably, Euler discovered the power series expansions for e, a base number for the exponential function with special characteristics, and also for the inverse tangent function.

A geometric interpretation of Euler's formula.

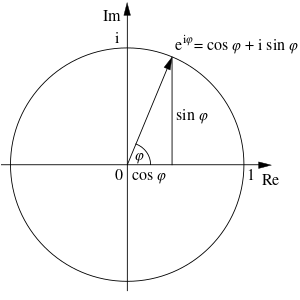
Euler introduced the use of the exponential function and logarithms in analytic proofs. He discovered ways to express various logarithmic functions in terms of power series, and successfully defined logarithms for negative and complex numbers, thus greatly expanding the scope where logarithms could be applied in mathematics. He also defined the exponential function for complex numbers and discovered its relation to the trigonometric functions. For any real number φ, Euler's formula states that the complex exponential function satisfies

$e^{i\phi }=\cos \phi +i\sin \phi \!.$

A special case of the above formula is known as Euler's identity,

$e^{i\pi }+1=0\,$

called "the most remarkable formula in mathematics" by twentieth century physicist Richard Feynman, for its single uses of the notions of addition, multiplication, exponentiation, and equality, and the single uses of the important constants 0, 1, e, i, and π.

Number theory

Euler's great interest in number theory can be traced to the influence of his friend in the St. Petersburg Academy, Christian Goldbach. A lot of his early work on number theory was based on the works of Pierre de Fermat. Euler developed some of Fermat's ideas while disproving some of his more outlandish conjectures.

One focus of Euler's work was to link the nature of prime distribution with ideas in analysis. He proved that the sum of the reciprocals of the primes diverges.

Graph theory

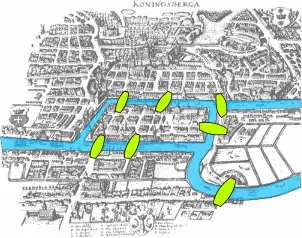
In 1736, Euler solved a problem known as the Seven Bridges of Königsberg. The city of Königsberg, Prussia (now Kaliningrad, Russia) is set on the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges. The question is whether it is possible to walk with a route that crosses each bridge exactly once, and return to the starting point. It is not; and therefore not an Eulerian circuit. This solution is considered to be the first theorem of graph theory and planar graph theory. Euler also introduced the notion now known as the Euler characteristic of a space and a formula relating the number of edges, vertices, and faces of a convex polyhedron with this constant. The study and generalization of this formula, specifically by Cauchy and L'Huillier, is at the origin of topology.

Applied mathematics

Euler integrated Leibniz's differential calculus with Newton's method of fluxions, and developed tools that made it easier to apply calculus to physical problems. He made great strides in improving methods of numerical approximation. One of Euler's more unusual interests was the application of mathematical ideas in music. In 1739 he wrote the Tentamen novae theoriae musicae, hoping to eventually integrate musical theory as part of mathematics. This part of his work, however, did not receive wide attention and was once described as too mathematical for musicians and too musical for mathematicians. Euler helped develop the Euler-Bernoulli beam equation, which became a cornerstone of engineering.

Physics and astronomy

Aside from successfully applying his analytic tools to problems in classical mechanics, Euler also applied these techniques to celestial problems. His work in astronomy was recognized by a number of Paris Academy Prizes over the course of his career. His accomplishments include determining with great accuracy the orbits of comets and other celestial bodies, understanding the nature of comets, and calculating the parallax of the sun. His calculations also contributed to the development of accurate longitude tables

In addition, Euler made important contributions in optics. He disagreed with Newton's corpuscular theory of light in the Opticks, which was then the prevailing theory. His 1740s papers on optics helped ensure that the wave theory of light proposed by Christian Huygens would become the dominant mode of thought, at least until the development of the quantum theory of light.

Logic

He is also credited with using closed curves to illustrate syllogistic reasoning (1768). These diagrams have become known as Euler diagrams.

Legacy

Euler is considered the most prolific mathematician of all time. His contributions made possible further advances by later mathematicians, including Joseph Louis Lagrange and Pierre-Simon Laplace.

Much of what is known of Euler's religious beliefs can be deduced from his Letters to a German Princess and an earlier work, Defense of the Divine Revelation against the Objections of the Freethinkers. These works present Euler as a staunch Christian and biblical literalist. David Brewster, a nineteenth-century physicist and Euler biographer, notes that Euler's fame and the disruptions in his life "never induced him to abandon the religious duties to which he had been educated. As long as he preserved his sight, he assembled the whole of his family every evening, and read a chapter of the Bible, which he accompanied with an exhortation."

One of his students, Nicholas von Fuss, observed that Euler's "piety was rational and sincere. His devotion was fervent. He was fully persuaded of the truth of Christianity. He felt its importance to the dignity and happiness of human nature, and looked on its detractors, and opposers, as the most pernicious enemies of man"

In light of Euler's strong religious bent, it is instructive to see how he was viewed by Frederick's court. When he was about leave Berlin for Saint Petersburg, Jean le Rond D'Alembert observed that Euler "is a man by no means amusing, but a very great mathematician." In the Court of Frederick at the height of the Enlightenment, it is understandable that Euler was unpopular. Frederick himself called Euler "a narrow-minded geometer whose ears were incapable of feeling the delicacy of poetry."

Lagrange had a very high regard for Euler's mathematical works, and numbered them among the few that he recommended to students. Euler broke new ground in the study of the infinitesimal calculus and its applications. He can be compared to Isaac Newton, who had strongly held religious beliefs. But Euler's scientific output did not seem to be impeded by the obligations of a large family, whereas it is often said that Newton could devote time to his researches only because he did not have a wife and children. Euler may be compared to Johann Sebastian Bach, who, although one of the most prolific composers of all time, and a contemporary of Euler, also enjoyed the obligations of a large family. Neither family nor religion, then, seems to have been an impediment to Euler's contributions to humankind, and these may very well have been a positive impetus to his level of accomplishment.

Selected list of Euler's publications

The cover page of Euler's Methodus inveniendi lineas curvas.

Euler has an extensive bibliography, but his best known books include the following:

• Elements of Algebra (1822). This elementary algebra text starts with a discussion of the nature of numbers and gives a comprehensive introduction to algebra, including formulae for solutions of polynomial equations.
• Introductio in analysin infinitorum (1748). English translation Introduction to Analysis of the Infinite, trand. by John Blanton (Book I, Springer-Verlag 1988, ISBN 0387968245; Book II, Springer-Verlag 1989, ISBN 0387971327).
• Two influential textbooks on calculus: Institutiones calculi differentialis (1755) and Institutiones calculi integralis (1768–1770).
• Lettres à une Princesse d'Allemagne (Letters to a German Princess) (1768-1772). (in French). English translation, with notes, and a life of Euler: Volume 1, Volume 2 Google Books. Retrieved January 24, 2023.
• Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744). The Latin title translates as a method for finding curved lines enjoying properties of maximum or minimum, or solution of isoperimetric problems in the broadest accepted sense.

A definitive collection of Euler's works, entitled Opera Omnia, has been published since 1911 by the Euler Committee of Swiss Academy of Science.

References

ISBN links support NWE through referral fees

• Boyer, Carl B., and Uta C. Merzbach. A History of Mathematics. New York: John Wiley & Sons, 1991. ISBN 0471543977
• Brewster, David. "A Life of Euler," in Letters on Different Subjects in Natural Philosophy: Addressed to a German Princess. New York: Harper & Brothers, 1837.
• Coulston, Charles (ed.). Dictionary of Scientific Biography. New York, Charles Scribner's Sons, 1981. ISBN 978-0684169620
• Dunham, William. Euler: The Master of Us All. Washington, DC: Mathematical Association of America, 1999. ISBN 0883853280
• Feynman, Richard. The Feynman Lectures on Physics: Volume I. Addison Wesley, 2005. ISBN 0805390456
• Horner, Francis. 1822. "Memoir of the Life and Character of Euler" in Leonhard Euler, Elements of Algebra, tr. Horner. London: Longman, Hurst, Rees, Orme and Co. 1: vii-xxii.
• James, Ioam. Remarkable Mathematicians: From Euler to von Neumann. (Cambridge, UK: Cambridge University Press, 2003. ISBN 0521520940
• Krus, D.J. Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics. Quality and Quantity: International Journal of Methodology 35 (2001): 445-446.
• Nahin, Paul. Dr. Euler's Fabulous Formula. Princeton: Princeton University Press, 2006. ISBN 9780691118222
• Simmons, John. The Giant Book of Scientists: The 100 greatest minds of all time. Sydney: The Book Company, 1996. ISBN 978-1854876959
• Singh, Simon. Fermat's last theorem. New York: Fourth Estate, 1997. ISBN 1857026691
• Stewart, James, Lothar Redlin, and Saleem Watson. Algebra and Trigonometry. Cengage Learning, 2015. ISBN 978-1305071742
• Thiele, Rüdiger. "The mathematics and science of Leonhard Euler," in Michael Kinyon and Glen van Brummelen (eds.). Mathematics and the Historian's Craft: The Kenneth O. May Lectures. CMS Books in Mathematics, Springer Verlag, 2005. ISBN 0387252843
• Thomson, Thomas (ed.). "Biographical Account of M. Le Comte Lagrange, by M. le Chavalier Delambre." Annals of Philosophy 3 (1814): 329.
• Towers, Joseph. Memoirs of the Life and Reign of Frederick the Third, King of Prussia. Forgotten Books, 2019 (original 1789). ISBN 0282058060
• Wanner, Gerhard, and Ernst Harrier. Analysis by its history. New York: Springer, 2005. ISBN 0387770313

External links

All links retrieved January 24, 2023.

• References for Leonhard Euler
• Leonhard Euler Tercentenary - Basel 2007
• The Euler Society.
• Leonhard Euler MacTutor

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Leonhard Euler  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Leonhard Euler"

Note: Some restrictions may apply to use of individual images which are separately licensed.