Exponential function

Graph of y = e^x. The exponential function is nearly flat (climbing slowly) for negative values of x, climbs quickly for positive values of x, and equals 1 when x is equal to 0. Its y value always equals the slope at that point.

The exponential function is one of the most important functions in mathematics. For a variable x, this function is written as exp(x) or e^x, where e is a mathematical constant, the base of the natural logarithm, which equals approximately 2.718281828, and is also known as Euler's number. Here, e is called the base and x is called the exponent. In a more general form, an exponential function can be written as a^x, where a is a constant and x is a variable.

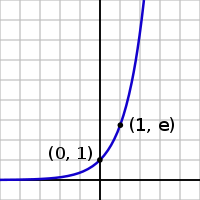
The graph of y = e^x is shown on the right. The graph is always positive (above the x axis) and increases from left to right. It never touches the x axis, although it gets extremely close to it. In other words, the x axis is a horizontal asymptote to the graph. Its inverse function, the logarithm, $\log _{e}(x)=y\,$, is defined for all positive x.

Sometimes, especially in the sciences, the term exponential function is more generally used for functions of the form ka^x, where a is any positive real number not equal to one.

In general, the variable x can be any real or complex number, or even an entirely different kind of mathematical object.

Some applications of the exponential function include modeling growth in populations, economic changes, fatigue of materials, and radioactive decay.

Properties

Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture that doubles every 20 minutes can be expressed (approximatively, as this is not really a continuous problem) as an exponential, as can the value of a car that decreases by 10 percent per year.

Using the natural logarithm, one can define more general exponential functions. The function

$\,\!\,a^{x}=(e^{\ln a})^{x}=e^{x\ln a}$

defined for all a > 0, and all real numbers x, is called the exponential function with base a. Note that this definition of $\,a^{x}$ rests on the previously established existence of the function $\,e^{x}$, defined for all real numbers.

Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following exponential laws:

$\,\!\,a^{0}=1$

$\,\!\,a^{1}=a$

$\,\!\,a^{x+y}=a^{x}a^{y}$

$\,\!\,a^{xy}=\left(a^{x}\right)^{y}$

$\,\!\,{1 \over a^{x}}=\left({1 \over a}\right)^{x}=a^{-x}$

$\,\!\,a^{x}b^{x}=(ab)^{x}$

These are valid for all positive real numbers a and b and all real numbers x and y. Expressions involving fractions and roots can often be simplified using exponential notation:

$\,{1 \over a}=a^{-1}$

and, for any a > 0, real number b, and integer n > 1:

$\,{\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}.$

Formal definition

The exponential function e^x can be defined in a variety of equivalent ways, as an infinite series. In particular, it may be defined by a power series:

$e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots$

or as the limit of a sequence:

$e^{x}=\lim _{n\to \infty }\left(1+{x \over n}\right)^{n}.$

In these definitions, n! stands for the factorial of n, and x can be any real number, complex number, element of a Banach algebra (for example, a square matrix), or member of the field of p-adic numbers.

Derivatives and differential equations

The importance of exponential functions in mathematics and the sciences stems mainly from properties of their derivatives. In particular,

$\,{d \over dx}e^{x}=e^{x}$

That is, e^x is its own derivative. Functions of the form $\,Ke^{x}$ for constant K are the only functions with that property. (This follows from the Picard-Lindelöf theorem, with $\,y(t)=e^{t},y(0)=K$ and $\,f(t,y(t))=y(t)$.) Other ways of saying the same thing include:

• The slope of the graph at any point is the height of the function at that point.
• The rate of increase of the function at x is equal to the value of the function at x.
• The function solves the differential equation $\,y'=y$.
• exp is a fixed point of derivative as a functional

In fact, many differential equations give rise to exponential functions, including the Schrödinger equation and the Laplace's equation as well as the equations for simple harmonic motion.

For exponential functions with other bases:

$\,{d \over dx}a^{x}=(\ln a)a^{x}$

Thus any exponential function is a constant multiple of its own derivative.

If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time.

Furthermore for any differentiable function f(x), we find, by the chain rule:

$\,{d \over dx}e^{f(x)}=f'(x)e^{f(x)}$.

Double exponential function

The term double exponential function can have two meanings:

• a function with two exponential terms, with different exponents
• a function $\,f(x)=a^{a^{x}}$; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 10¹⁰, f(2) = 10¹⁰⁰ = googol, ..., f(100) = googolplex.

Factorials grow faster than exponential functions, but slower than double-exponential functions. Fermat numbers, generated by $\,F(m)=2^{2^{m}}+1$ and double Mersenne numbers generated by $\,MM(p)=2^{(2^{p}-1)}-1$ are examples of double exponential functions.

See also

• Logarithm
• Radioactive decay

References

ISBN links support NWE through referral fees

• Carico, Charles C. 1974. Exponential and logarithmic functions (Wadsworth precalculus mathematics series). Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141.
• Fried, H. M. 2002. Green's Functions and Ordered Exponentials. Cambridge, UK: Cambridge University Press. ISBN 0521443903.
• Konyagin, Sergei, and Igor Shparlinski. 1999. Character Sums with Exponential Functions and their Applications. Cambridge, UK: Cambridge University Press. ISBN 0521642639.

External links

All links retrieved March 23, 2024.

• Complex exponential function.
• Derivative of exponential function.
• Exponential Function.
• Taylor Series Expansions of Exponential Functions – efunda.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Exponential function  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Exponential function"

Note: Some restrictions may apply to use of individual images which are separately licensed.