Logarithm

Logarithms to various bases: red is to base e, green is to base 10, and purple is to base 1.7. Each tick on the axes is one unit. Logarithms of all bases pass through the point (1, 0), because any number raised to the power 0 is 1, and through the points (b, 1) for base b, because any number raised to the power 1 is itself. The curves approach the y axis but do not reach it, due to the singularity of a logarithm at x = 0.

In mathematics, the logarithm (or log) of a number x in base b is the power (n) to which the base b must be raised to obtain the number x. For example, the logarithm of 1000 to the base 10 is the number 3, because 10 raised to the power of 3 is 1000. Or, the logarithm of 81 to the base 3 is 4, because 3 raised to the power of 4 is 81.

In general terms, if x = bⁿ, then the logarithm of x in base b is usually written as

$\log _{b}(x)=n.\,$

(The value b must be neither 0 nor the root of 1.)

A useful way of remembering this concept is by asking: "b to what power (n) equals x?" When x and b are restricted to positive real numbers, the logarithm is a unique real number.

Using one of the examples noted above, 3 raised to the power of 4 is usually written as

$3^{4}=3\times 3\times 3\times 3=81\,$

In logarithmic terms, one would write this as

$\log _{3}(81)=4\,$

In words, the base-3 logarithm of 81 is 4; or the log base-3 of 81 is 4.

The most widely used bases for logarithms are 10, the mathematical constant e (approximately equal to 2.71828), and 2. The term common logarithm is used when the base is 10; the term natural logarithm is used when the base is e.

The method of logarithms simplifies certain calculations and is used in expressing various quantities in science. For example, before the advent of calculators and computers, the method of logarithms was very useful for the advance of astronomy, and for navigation and surveying. Number sequences written on logarithmic scales continue to be used by scientists in various disciplines. Examples of logarithmic scales include the pH scale, to measure acidity (or basicity) in chemistry; the Richter scale, to measure earthquake intensity; and the scale expressing the apparent magnitude of stars, to indicate their brightness.

The inverse of the logarithmic function is called the antilogarithm function. It is written as antilog_b(n), and it means the same as $b^{n}$.

History

The method of logarithms was first publicly propounded in 1614, in a book titled Mirifici Logarithmorum Canonis Descriptio, by John Napier, Baron of Merchiston in Scotland. (Joost Bürgi, independently discovered logarithms, but he did not publish his discovery until four years after Napier.)

This method contributed to the advance of science, and especially of astronomy, by making some difficult calculations possible. Prior to the advent of calculators and computers, it was used constantly in surveying, navigation, and other branches of practical mathematics. It supplanted the more involved method of prosthaphaeresis, which relied on trigonometric identities as a quick method of computing products. Besides their usefulness in computation, logarithms also fill an important place in higher theoretical mathematics.

At first, Napier called logarithms "artificial numbers" and antilogarithms "natural numbers." Later, he formed the word logarithm to mean a number that indicates a ratio: λόγος (logos) meaning proportion, and ἀριθμός (arithmos) meaning number. Napier chose that because the difference of two logarithms determines the ratio of the numbers for which they stand, so that an arithmetic series of logarithms corresponds to a geometric series of numbers. The term "antilogarithm" was introduced in the late seventeenth century and, while never used extensively in mathematics, persisted in collections of tables until they fell into disuse.

Napier did not use a base as we now understand it, but his logarithms were, up to a scaling factor, effectively to base 1/e. For interpolation purposes and ease of calculation, it is useful to make the ratio r in the geometric series close to 1. Napier chose r = 1 - 10⁻⁷ = 0.999999 (Bürgi chose r = 1 + 10⁻⁴ = 1.0001). Napier's original logarithms did not have log 1 = 0 but rather log 10⁷ = 0. Thus if N is a number and L is its logarithm as calculated by Napier, N = 10⁷(1 − 10⁻⁷)^L. Since (1 − 10⁻⁷)¹⁰⁷ is approximately 1/e, this makes L/10⁷ approximately equal to log_1/e N/10⁷.

Tables of logarithms

Part of a twentieth-century table of common logarithms in the reference book Abramowitz and Stegun.

Prior to the advent of computers and calculators, using logarithms meant using tables of logarithms, which had to be created manually. Base-10 logarithms are useful in computations when electronic means are not available.

In 1617, Henry Briggs published the first installment of his own table of common logarithms, containing the logarithms of all integers below 1000 to eight decimal places. This he followed, in 1624, with his Arithmetica Logarithmica, containing the logarithms of all integers from 1 to 20,000 and from 90,000 to 100,000 to fourteen places of decimals, together with a learned introduction, in which the theory and use of logarithms were fully developed.

The interval from 20,000 to 90,000 was filled by Adriaan Vlacq, a Dutch mathematician; but in his table, which appeared in 1628, the logarithms were given to only ten places of decimals. Vlacq's table was later found to contain 603 errors, but "this cannot be regarded as a great number, when it is considered that the table was the result of an original calculation, and that more than 2,100,000 printed figures are liable to error." An edition of Vlacq's work, containing many corrections, was issued at Leipzig in 1794, under the title Thesaurus Logarithmorum Completus by Jurij Vega.

François Callet's seven-place table (Paris, 1795), instead of stopping at 100,000, gave the eight-place logarithms of the numbers between 100,000 and 108,000, in order to diminish the errors of interpolation, which were greatest in the early part of the table; and this addition was generally included in seven-place tables. The only important published extension of Vlacq's table was made by Mr. Sang 1871, whose table contained the seven-place logarithms of all numbers below 200,000.

Briggs and Vlacq also published original tables of the logarithms of the trigonometric functions.

Besides the tables mentioned above, a great collection, called Tables du Cadastre, was constructed under the direction of Gaspard de Prony, by an original computation, under the auspices of the French republican government of the 1700s. This work, which contained the logarithms of all numbers up to 100,000 to nineteen places, and of the numbers between 100,000 and 200,000 to twenty-four places, exists only in manuscript, "in seventeen enormous folios," at the Observatory of Paris. It was begun in 1792; and "the whole of the calculations, which to secure greater accuracy were performed in duplicate, and the two manuscripts subsequently collated with care, were completed in the short space of two years." Cubic interpolation could be used to find the logarithm of any number to a similar accuracy.

The logarithm as a function

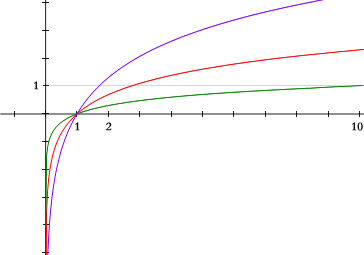
The function log_b(x) depends on both b and x, but the term logarithm function (or logarithmic function) in standard usage refers to a function of the form log_b(x) in which the base b is fixed and so the only argument is x. Thus there is one logarithm function for each value of the base b (which must be positive and must differ from 1). Viewed in this way, the base-b logarithm function is the inverse function of the exponential function b^x. The word "logarithm" is often used to refer to a logarithm function itself as well as to particular values of this function.

Graphical interpretation

The natural logarithm of a is the area under the curve y = 1/x between the x values 1 and a.

Irrationality

For integers b and x > 1, the number log_b(x) is irrational (that is, not a quotient of two integers) if either b or x has a prime factor which the other does not. In certain cases this fact can be proved very quickly: for example, if log₂3 were rational, we would have log₂3 = n/m for some positive integers n and m, thus implying 2ⁿ = 3^m. But this last identity is impossible, since 2ⁿ is even and 3^m is odd. Much stronger results are known. See Lindemann–Weierstrass theorem.

Integer and non-integer exponents

If n is a positive integer, bⁿ signifies the product of n factors equal to b:

$\underbrace {b\times b\times \cdots \times b} _{n}.$

However, if b is a positive real number not equal to 1, this definition can be extended to any real number n in a field (see exponentiation). Similarly, the logarithm function can be defined for any positive real number. For each positive base b not equal to 1, there is one logarithm function and one exponential function, which are inverses of each other.

Logarithms can reduce multiplication operations to addition, division to subtraction, exponentiation to multiplication, and roots to division. Therefore, logarithms are useful for making lengthy numerical operations easier to perform and, before the advent of electronic computers, they were widely used for this purpose in fields such as astronomy, engineering, navigation, and cartography. They have important mathematical properties and are still widely used today.

Bases

The most widely used bases for logarithms are 10, the mathematical constant e ≈ 2.71828… and 2. When "log" is written without a base (b missing from log_b), the intent can usually be determined from context:

• Natural logarithm (log_e, ln, log, or Ln) in mathematical analysis
• Common logarithm (log₁₀ or simply log) in engineering and when logarithm tables are used to simplify hand calculations
• Binary logarithm (log₂) in information theory and musical intervals
• Indefinite logarithm when the base is irrelevant, for example, in complexity theory when describing the asymptotic behavior of algorithms in big O notation.

To avoid confusion, it is best to specify the base if there is any chance of misinterpretation.

Other notations

The notation "ln(x)" invariably means log_e(x), that is, the natural logarithm of x, but the implied base for "log(x)" varies by discipline:

• Mathematicians generally understand both "ln(x)" and "log(x)" to mean log_e(x) and write "log₁₀(x)" when the base-10 logarithm of x is intended.

• Many engineers, biologists, astronomers, and some others write only "ln(x)" or "log_e(x)" when they mean the natural logarithm of x, and take "log(x)" to mean log₁₀(x) or, sometimes in the context of computing, log₂(x).

• On most calculators, the LOG button is log₁₀(x) and LN is log_e(x).

• In most commonly used computer programming languages, including C, C++, Java, Fortran, Ruby, and BASIC, the "log" function returns the natural logarithm. The base-10 function, if it is available, is generally "log10."

• Some people use Log(x) (capital L) to mean log₁₀(x), and use log(x) with a lowercase l to mean log_e(x).

• The notation Log(x) is also used by mathematicians to denote the principal branch of the (natural) logarithm function.

• A notation frequently used in some European countries is the notation ^blog(x) instead of log_b(x).

This chaos, historically, originates from the fact that the natural logarithm has nice mathematical properties (such as its derivative being 1/x, and having a simple definition), while the base 10 logarithms, or decimal logarithms, were more convenient for speeding calculations (back when they were used for that purpose). Thus, natural logarithms were only extensively used in fields like calculus while decimal logarithms were widely used elsewhere.

As recently as 1984, Paul Halmos in his "automathography" I Want to Be a Mathematician heaped contempt on what he considered the childish "ln" notation, which he said no mathematician had ever used. (The notation was in fact invented in 1893 by Irving Stringham, professor of mathematics at Berkeley.) As of 2005, many mathematicians have adopted the "ln" notation, but most use "log."

In computer science, the base 2 logarithm is sometimes written as lg(x) to avoid confusion. This usage was suggested by Edward Reingold and popularized by Donald Knuth. However, in Russian literature, the notation lg(x) is generally used for the base 10 logarithm, so even this usage is not without its perils. In German, lg(x) also denotes the base 10 logarithm, while sometimes ld(x) or lb(x) is used for the base 2 logarithm.

Change of base

While there are several useful identities, the most important for calculator use lets one find logarithms with bases other than those built into the calculator (usually log_e and log₁₀). To find a logarithm with base b, using any other base k:

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.$

Moreover, this result implies that all logarithm functions (whatever the base) are similar to each other. So to calculate the log with base 2 of the number 16 with your calculator:

$\log _{2}(16)={\frac {\log(16)}{\log(2)}}.$

Uses of logarithms

Logarithms are useful in solving equations in which exponents are unknown. They have simple derivatives, so they are often used in the solution of integrals. The logarithm is one of three closely related functions. In the equation bⁿ = x, b can be determined with radicals, n with logarithms, and x with exponentials. See logarithmic identities for several rules governing the logarithm functions. For a discussion of some additional aspects of logarithms see additional logarithm topics.

Science and engineering

Various quantities in science are expressed as logarithms of other quantities.

• The negative of the base-10 logarithm is used in chemistry, where it expresses the concentration of hydronium ions (H₃O⁺, the form H⁺ takes in water), in the measure known as pH. The concentration of hydronium ions in neutral water is 10⁻⁷ mol/L at 25 °C, hence a pH of 7.

• The bel (symbol B) is a unit of measure that is the base-10 logarithm of ratios, such as power levels and voltage levels. It is mostly used in telecommunication, electronics, and acoustics. It is used, in part, because the ear responds logarithmically to acoustic power. The Bel is named after telecommunications pioneer Alexander Graham Bell. The decibel (dB), equal to 0.1 bel, is more commonly used. The neper is a similar unit which uses the natural logarithm of a ratio.

• The Richter scale measures earthquake intensity on a base-10 logarithmic scale.

• In spectrometry and optics, the absorbance unit used to measure optical density is equivalent to −1 B.

• In astronomy, the apparent magnitude measures the brightness of stars logarithmically, since the eye also responds logarithmically to brightness.

• In psychophysics, the Weber–Fechner law proposes a logarithmic relationship between stimulus and sensation.

• In computer science, logarithms often appear in bounds for computational complexity. For example, to sort N items using comparison can require time proportional to N log N.

Exponential functions

The natural exponential function exp(x), also written $e^{x}$ is defined as the inverse of the natural logarithm. It is positive for every real argument x.

The operation of "raising b to a power p" for positive arguments $b$ and all real exponents $p$ is defined by

$b^{p}=\exp({p\ln b}).\,$

The antilogarithm function is another name for the inverse of the logarithmic function. It is written antilog_b(n) and means the same as $b^{n}$.

Easier computations

Logarithms switch the focus from normal numbers to exponents. As long as the same base is used, this makes certain operations easier:

Operation with numbers	Operation with exponents	Logarithmic identity
$\!\,ab$	$\!\,A+B$	$\!\,\log(ab)=\log(a)+\log(b)$
$\!\,a/b$	$\!\,A-B$	$\!\,\log(a/b)=\log(a)-\log(b)$
$\!\,a^{b}$	$\!\,Ab$	$\!\,\log(a^{b})=b\log(a)$
$\!\,{\sqrt[{b}]{a}}$	$\!\,A/b$	$\!\,\log({\sqrt[{b}]{a}})={\frac {\log(a)}{b}}$

These relations made such operations on two numbers much faster and the proper use of logarithms was an essential skill before multiplying calculators became available.

The $\log(ab)=\log(a)+\log(b)$ equation is fundamental (it implies effectively the other three relations in a field) because it describes an isomorphism between the additive group and the multiplicative group of the field.

To multiply two numbers, one found the logarithms of both numbers on a table of common logarithms, added them, and then looked up the result in the table to find the product. This is faster than multiplying them by hand, provided that more than two decimal figures are needed in the result. The table needed to get an accuracy of seven decimals could be fit in a big book, and the table for nine decimals occupied a few shelves.

The discovery of logarithms just before Newton's era had an impact in the scientific world which can be compared with the invention of the computer in the twentieth century, because many calculations which were too laborious became feasible.

When the chronometer was invented in the eighteenth century, logarithms allowed all calculations needed for astronomical navigation to be reduced to just additions, speeding the process by one or two orders of magnitude. A table of logarithms with five decimals, plus logarithms of trigonometric functions, was enough for most astronomical navigation calculations, and those tables fit in a small book.

To compute powers or roots of a number, the common logarithm of that number was looked up and multiplied or divided by the radix. Interpolation could be used for still higher precision. Slide rules used logarithms to perform the same operations more rapidly, but with much less precision than using tables. Other tools for performing multiplications before the invention of the calculator include Napier's bones and mechanical calculators: see history of computing hardware.

Calculus

The derivative of the natural logarithm function is

${\frac {d}{dx}}\ln(x)={\frac {1}{x}}.$ (A proof is shown below.)

By applying the change-of-base rule, the derivative for other bases is

${\frac {d}{dx}}\log _{b}(x)={\frac {d}{dx}}{\frac {\ln(x)}{\ln(b)}}={\frac {1}{x\ln(b)}}={\frac {\log _{b}(e)}{x}}.$

The antiderivative of the logarithm is

$\int \log _{b}(x)\,dx=x\log _{b}(x)-{\frac {x}{\ln(b)}}+C=x\log _{b}\left({\frac {x}{e}}\right)+C.$

See also: table of limits of logarithmic functions, list of integrals of logarithmic functions.

Proof of the derivative

The derivative of the natural logarithm function is easily found via the inverse function rule. Since the inverse of the logarithm function is the exponential function, we have $\ln '(x)={\frac {1}{\exp '(\ln(x))}}$. Since the derivative of the exponential function is itself, the right side of the equation simplifies to ${\frac {1}{\exp(\ln(x))}}={\frac {1}{x}}$, the exponential canceling out the logarithm.

Computers

When considering computers, the usual case is that the argument and result of the $\ln(x)$ function is some form of floating point data type. Note that most computer languages uses $\log(x)$ for this function while the $\log _{10}(x)$ is typically denoted log10(x).

As the argument is floating point, it can be useful to consider the following:

A floating point value x is represented by a mantissa m and exponent n to form

$x=m2^{n}.\,$

Therefore

$\ln(x)=\ln(m)+n\ln(2).\,$

Thus, instead of computing $\ln(x)$ we compute $\ln(m)$ for some m such that $1\leq m<2$. Having $m$ in this range means that the value $u={\frac {m-1}{m+1}}$ is always in the range $0\leq u<{\frac {1}{3}}$. Some machines uses the mantissa in the range $0.5\leq m<1$ and in that case the value for u will be in the range $-{\frac {1}{3}}<u\leq 0$ In either case, the series is even easier to compute.

Generalizations

The ordinary logarithm of positive reals generalizes to negative and complex arguments, though it is a multivalued function that needs a branch cut terminating at the branch point at 0 to make an ordinary function or principal branch. The logarithm (to base e) of a complex number z is the complex number ln(|z|) + i arg(z), where |z| is the modulus of z, arg(z) is the argument, and i is the imaginary unit.

The discrete logarithm is a related notion in the theory of finite groups. It involves solving the equation bⁿ = x, where b and x are elements of the group, and n is an integer specifying a power in the group operation. For some finite groups, it is believed that the discrete logarithm is very hard to calculate, whereas discrete exponentials are quite easy. This asymmetry has applications in public key cryptography.

The logarithm of a matrix is the inverse of the matrix exponential.

A double logarithm, $\ln(\ln(x))$, is the inverse function of the double exponential function. A super-logarithm or hyper-logarithm is the inverse function of the super-exponential function. The super-logarithm of x grows even more slowly than the double logarithm for large x.

For each positive b not equal to 1, the function log_b  (x) is an isomorphism from the group of positive real numbers under multiplication to the group of (all) real numbers under addition. They are the only such isomorphisms that are continuous. The logarithm function can be extended to a Haar measure in the topological group of positive real numbers under multiplication.

References

ISBN links support NWE through referral fees

• Great Britain Institute of Actuaries, Journal of the Institute of Actuaries and Assurance Magazine, 1873, Vol. 17. Forgotten Books, 2018. 978-0366971244
• Knight, Charles. The English Cyclopaedia, Vol. 4. Forgotten Books, 2012.
• Peirce, James Mills. The Elements of Logarithms with an Explanation of the Three and Four Place Tables of Logarithmic and Trigonometric Functions. Andesite Press, 2015. ISBN 978-1297495465
• Przeworska-Rolewicz, D. Logarithms and Antilogarithms: An Algebraic Analysis Approach with an appendix by Zbigniew Binderman (Mathematics and Its Applications). New York, NY: Springer, 1998. ISBN 0792349741.
• REA. Math Made Nice & Easy #2: Percentages, Exponents, Radicals, Logarithms and Algebra Basics (Math Made Nice & Easy). Piscataway, NJ: Research & Education Association, 1999. ISBN 0878912010.
• Ryffel, Henry, Robert Green, Holbrook Horton, and Edward Messal. Mathematics at Work. New York, NY: Industrial Press, Inc., 1999. ISBN 0831130830.

External links

All links retrieved November 3, 2022.

• Explaining Math Logarithms.
• Logarithm on MathWorld.
• Jost Burgi, Swiss Inventor of Logarithms.
• Logarithm calculators and word problems with work shown, for school students.
• Logarithms - from The Little Handbook of Statistical Practice.
• Logarithmic Functions

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Logarithm  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Logarithm"

Note: Some restrictions may apply to use of individual images which are separately licensed.