Fraction (mathematics)

A cake with one quarter removed. The remaining three quarters are shown.

In mathematics, a fraction (from the Latin fractus, broken) is a concept of a proportional relation between an object part and the object whole. A fraction is an example of a specific type of ratio, in which the two numbers are related in a part-to-whole relationship, rather than as a comparative relation between two separate quantities. A fraction is a quotient of numbers, the quantity obtained when the numerator is divided by the denominator.

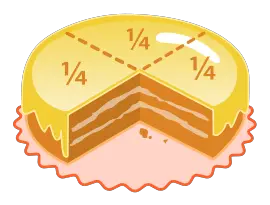
For example, ³⁄₄ represents three divided by four, which may be represented as the decimal term 0.75, or as the percentage, 75 percent. The three equal parts out of the overall possible four equal parts assigned, therefore, constitute 75 percent of the whole cake. In other words, the fraction ³⁄₄ could be used to represent three equal parts of a whole object, were it divided into four equal parts.

Each fraction consists of a denominator (bottom) and a numerator (top), representing (respectively) the number of equal parts that an object is divided into, and the number of those parts indicated for the particular fraction. Fractions are rational numbers, which means that the denominator and the numerator are integers. A fraction with equal numerator and denominator is equal to one (e.g. ⁵⁄₅ = 1) and the fraction form is rarely, if ever, given as a final result. Because it is impossible to divide something into zero equal parts, zero can never be the denominator of a fraction (see division by zero).

In higher mathematics, a fraction is viewed as an element of a field of fractions.

Terminology

Historically, any number that did not represent a whole was called a "fraction." The numbers that we now call "decimals" were originally called "decimal fractions"; the numbers we now call "fractions" were called "vulgar fractions," the word "vulgar" meaning "commonplace."

The word is also used in related expressions, such as continued fraction and algebraic fraction—see Special cases below.

Writing fractions

The numerator and denominator of a fraction may be separated by a slanting line called a solidus or slash, for example ³⁄₄, or may be written above and below a horizontal line called a vinculum, thus: ${\tfrac {3}{4}}$.

The solidus may be omitted from the slanting style (e.g. ³₄) where space is short and the meaning is obvious from context, for example in road signs in some countries.

Reading fractions

Usually there are several ways to read fractions. One may say "three quarters" for ³⁄₄ and "one sixth" for ¹⁄₆. In strictly mathematical contexts these fractions might also be read as "three over four," "one over six" or "three upon four" resp. "one upon six," or "three out of four," etc.

Usage

Fractions are used most often when the denominator is relatively small. It is easier to multiply 32 by ³⁄₁₆ than to do the same calculation using the fraction's decimal equivalent (0.1875). It is also more accurate to multiply 15 by ¹⁄₃, for example, than it is to multiply 15 by a decimal approximation of one third. To change a fraction to a decimal, divide the numerator by the denominator, and round off to the desired accuracy.

Forms of fractions

Vulgar, proper, and improper fractions

A vulgar fraction (or common fraction) is a rational number written as one integer (the numerator) divided by a non-zero integer (the denominator).

A vulgar fraction is said to be a proper fraction if the absolute value of the numerator is less than the absolute value of the denominator—that is, if the absolute value of the entire fraction is less than 1; but an improper fraction (US, British or Australian) or top-heavy fraction (British, occasionally N.Am.) if the absolute value of the numerator is greater than or equal to the absolute value of the denominator (e.g. ⁹⁄₇).

Mixed numbers

A mixed number is the sum of a whole number and a proper fraction. This sum is implied without the use of any visible operator such as "+"; for instance, in referring to two entire cakes and three quarters of another cake, the whole and fractional parts of the number are written next to each other: $2+{\tfrac {3}{4}}=2{\tfrac {3}{4}}$.

An improper fraction can be thought of as another way to write a mixed number; in the "$2{\tfrac {3}{4}}$" example above, imagine that the two entire cakes are each divided into quarters. Each entire cake contributes ${\tfrac {4}{4}}$ to the total, so ${\tfrac {4}{4}}+{\tfrac {4}{4}}+{\tfrac {3}{4}}={\tfrac {11}{4}}$ is another way of writing $2{\tfrac {3}{4}}$.

A mixed number can be converted to an improper fraction in three steps:

1. Multiply the whole part by the denominator of the fractional part.
2. Add the numerator of the fractional part to that product.
3. The resulting sum is the numerator of the new (improper) fraction, with the 'new' denominator remaining precisely the same as for the original fractional part of the mixed number.

Similarly, an improper fraction can be converted to a mixed number:

1. Divide the numerator by the denominator.
2. The quotient (without remainder) becomes the whole part and the remainder becomes the numerator of the fractional part.
3. The new denominator is the same as that of the original improper fraction.

Equivalent fractions

Multiplying the numerator and denominator of a fraction by the same (non-zero) number, the results of the new fraction is said to be equivalent to the original fraction. The word equivalent means that the two fractions have the same value. That is, they retain the same integrity - the same balance or proportion. This is true because for any number $n$, multiplying by ${\tfrac {n}{n}}$ is really multiplying by one, and any number multiplied by one has the same value as the original number. For instance, consider the fraction ${\tfrac {1}{2}}$: when the numerator and denominator are both multiplied by 2, the result is ${\tfrac {2}{4}}$, which has the same value (0.5) as ${\tfrac {1}{2}}$. To picture this visually, imagine cutting the example cake into four pieces; two of the pieces together (${\tfrac {2}{4}}$) make up half the cake (${\tfrac {1}{2}}$).

For example: ${\tfrac {1}{4}}$, ${\tfrac {2}{8}}$, ${\tfrac {3}{12}}$ and ${\tfrac {100}{400}}$ are all equivalent fractions.

Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. this is called reducing or simplifying the fraction. A fraction in which the numerator and denominator have no factors in common (other than 1) is said to be irreducible or in its lowest or simplest terms. For instance, ${\tfrac {3}{9}}$ is not in lowest terms because both 3 and 9 can be exactly divided by 3. In contrast, ${\tfrac {3}{8}}$ is in lowest terms—the only number that is a factor of both 3 and 8 is 1.

Reciprocals and the "invisible denominator"

The reciprocal of a fraction is another fraction with the numerator and denominator reversed. The reciprocal of ${\tfrac {3}{7}}$, for instance, is ${\tfrac {7}{3}}$.

Because any number divided by 1 results in the same number, it is possible to write any whole number as a fraction by using 1 as the denominator: 17 = ${\tfrac {17}{1}}$ (1 is sometimes referred to as the "invisible denominator"). Therefore, except for zero, every fraction or whole number has a reciprocal. The reciprocal of 17 would be ${\tfrac {1}{17}}$.

Complex fractions

A complex fraction (or compound fraction) is a fraction in which the numerator or denominator contains a fraction. For example, ${\cfrac {\tfrac {1}{2}}{\tfrac {1}{3}}}$ is a complex fraction. To simplify a complex fraction, divide the numerator by the denominator, as with any other fraction (see the section on division for more details):

${\cfrac {\tfrac {1}{2}}{\tfrac {1}{3}}}={\tfrac {1}{2}}\times {\tfrac {3}{1}}={\tfrac {3}{2}}.$

${\cfrac {\tfrac {3}{2}}{5}}={\tfrac {3}{2}}\times {\tfrac {1}{5}}={\tfrac {3}{10}}.$

${\cfrac {8}{\tfrac {1}{3}}}=8\times {\tfrac {3}{1}}=24.$

Arithmetic with fractions

Fractions, like whole numbers, obey the commutative, associative, and distributive laws, and the rule against division by zero.

Comparing fractions

Comparing fractions with the same denominator only requires comparing the numerators.

${\tfrac {3}{4}}>{\tfrac {2}{4}}$ as $3>2$.

In order to compare fractions with different denominators, these are converted to a common denominator: to compare ${\tfrac {a}{b}}$ and ${\tfrac {c}{d}}$, these are converted to ${\tfrac {ad}{bd}}$ and ${\tfrac {bc}{bd}}$, where bd is the product of the denominators, and then the numerators ad and bc are compared.

${\tfrac {2}{3}}$ ? ${\tfrac {1}{2}}$ gives ${\tfrac {4}{6}}$>${\tfrac {3}{6}}$

This method is also known as the "cross-multiply" method which can be explained by multiplying the top and bottom numbers crosswise. The product of the denominators is used as a common (but not necessarily the least common) denominator.

${\tfrac {5}{18}}$ ? ${\tfrac {4}{17}}$

Multiply 17 by 5 and 18 by 4. Place the products of the equations on top of the denominators. The highest number identifies the largest fraction. Therefore ${\tfrac {5}{18}}>{\tfrac {4}{17}}$ as 17 × 5 = 85 is greater than 18 × 4 = 72.

In order to work with smaller numbers, the least common denominator is used instead of the product. The fractions are converted to fractions with the least common denominator, and then the numerators are compared.

${\tfrac {5}{6}}$ ? ${\tfrac {3}{4}}$ gives ${\tfrac {10}{12}}>{\tfrac {9}{12}}$

Addition

The first rule of addition is that only like quantities can be added; for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below: Imagine a pocket containing two quarters, and another pocket containing three quarters; in total, there are five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows:

${\tfrac {2}{4}}+{\tfrac {3}{4}}={\tfrac {5}{4}}=1{\tfrac {1}{4}}$.

If ${\tfrac {1}{2}}$ of a cake is to be added to ${\tfrac {1}{4}}$ of a cake, the pieces need to be converted into comparable quantities, such as cake-eighths or cake-quarters.

Adding unlike quantities

To add fractions containing unlike quantities (e.g. quarters and thirds), it is necessary to convert all amounts to like quantities. It is easy to work out the type of fraction to convert to; simply multiply together the two denominators (bottom number) of each fraction.

For adding quarters to thirds, both types of fraction are converted to ${\tfrac {1}{4}}\times {\tfrac {1}{3}}={\tfrac {1}{12}}$ (twelfths).

Consider adding the following two quantities:

${\tfrac {3}{4}}+{\tfrac {2}{3}}$

First, convert ${\tfrac {3}{4}}$ into twelfths by multiplying both the numerator and denominator by three: ${\tfrac {3}{4}}\times {\tfrac {3}{3}}={\tfrac {9}{12}}$. Note that ${\tfrac {3}{3}}$ is equivalent to 1, which shows that ${\tfrac {3}{4}}$ is equivalent to the resulting ${\tfrac {9}{12}}$

Secondly, convert ${\tfrac {2}{3}}$ into twelfths by multiplying both the numerator and denominator by four: ${\tfrac {2}{3}}\times {\tfrac {4}{4}}={\tfrac {8}{12}}$. Note that ${\tfrac {4}{4}}$ is equivalent to 1, which shows that ${\tfrac {2}{3}}$ is equivalent to the resulting ${\tfrac {8}{12}}$

Now it can be seen that:

${\tfrac {3}{4}}+{\tfrac {2}{3}}$

is equivalent to:

${\tfrac {9}{12}}+{\tfrac {8}{12}}={\tfrac {17}{12}}=1{\tfrac {5}{12}}$

This method always works, but sometimes there is a smaller denominator that can be used (a least common denominator). For example, to add ${\tfrac {3}{4}}$ and ${\tfrac {5}{12}}$ the denominator 48 can be used (the product of 4 and 12), but the smaller denominator 12 may also be used, being the least common multiple of 4 and 12.

${\tfrac {3}{4}}+{\tfrac {5}{12}}={\tfrac {9}{12}}+{\tfrac {5}{12}}={\tfrac {14}{12}}={\tfrac {7}{6}}=1{\tfrac {1}{6}}$

Subtraction

The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance,

${\tfrac {2}{3}}-{\tfrac {1}{2}}={\tfrac {4}{6}}-{\tfrac {3}{6}}={\tfrac {1}{6}}$

Multiplication

When multiplying or dividing, it may be possible to choose to cancel down crosswise multiples (often simply called, 'cancelling tops and bottom lines') that share a common factor. For example:

²⁄₇ X ⁷⁄₈ = ^{2 1}⁄_{7 1} X ^{7 1}⁄_{8 4} = ¹⁄₁ X ¹⁄₄ = ¹⁄₄

A two is a common factor in both the numerator of the left fraction and the denominator of the right so is divided out of both. A seven is a common factor of the left denominator and right numerator.

Whole numbers

Considering the cake example above, if you have a quarter of the cake and you multiply the amount by three, then you end up with three quarters. We can write this numerically as follows:

$\textstyle {3\times {1 \over 4}={3 \over 4}}\,\!$

As another example, suppose that five people work for three hours out of a seven hour day (i.e. for three sevenths of the work day). In total, they will have worked for 15 hours (5 x 3 hours each), or 15 sevenths of a day. Since 7 sevenths of a day is a whole day and 14 sevenths is two days, then in total, they will have worked for 2 days and a seventh of a day. Numerically:

$\textstyle {5\times {3 \over 7}={15 \over 7}=2{1 \over 7}}\,\!$

Fractions

Considering the cake example above, if you have a quarter of the cake and you multiply the amount by a third, then you end up with a twelfth of the cake. In other words, a third of a quarter (or a third times a quarter) is a twelfth. Why? Because we are splitting each quarter into three pieces, and four quarters times three makes 12 parts (or twelfths). We can write this numerically as follows:

$\textstyle {{1 \over 3}\times {1 \over 4}={1 \over 12}}\,\!$

As another example, suppose that five people do an equal amount of work that totals three hours out of a seven hour day. Each person will have done a fifth of the work, so they will have worked for a fifth of three sevenths of a day. Numerically:

$\textstyle {{1 \over 5}\times {3 \over 7}={3 \over 35}}\,\!$

General rule

You may have noticed that when we multiply fractions, we multiply the two numerators (the top numbers) to make the new numerator, and multiply the two denominators (the bottom numbers) to make the new denominator. For example:

$\textstyle {{5 \over 6}\times {7 \over 8}={5\times 7 \over 6\times 8}={35 \over 48}}\,\!$

Mixed numbers

When multiplying mixed numbers, it's best to convert the mixed number into an improper fraction. For example:

$\textstyle {3\times 2{3 \over 4}=3\times \left({{8 \over 4}+{3 \over 4}}\right)=3\times {11 \over 4}={33 \over 4}=8{1 \over 4}}\,\!$

In other words, $\textstyle {2{3 \over 4}}$ is the same as $\textstyle {({8 \over 4}+{3 \over 4})}$, making 11 quarters in total (because 2 cakes, each split into quarters makes 8 quarters total) and 33 quarters is $\textstyle {8{1 \over 4}}$, since 8 cakes, each made of quarters, is 32 quarters in total).

Division

To divide by a fraction, simply multiply by the reciprocal of that fraction.

$\textstyle {5\div {1 \over 2}=5\times {2 \over 1}=5\times 2=10}$

$\textstyle {{2 \over 3}\div {2 \over 5}={2 \over 3}\times {5 \over 2}={10 \over 6}={5 \over 3}}$

To understand why this works, consider the following:

6 inches divided by 3 inches = 2 means that we can divide 6 inches into two 3 inch parts.

6 miles divided by 3 miles = 2 means that we can divide 6 miles into two 3 mile parts.

6 half dollars divided by 3 half dollars = 2 means that we can divide 6 half dollars into two stacks of 3 half dollars each.

6/2 divided by 3/2 = 2 means that we can divide 6/2 into two parts, each 3/2 in size.

Thus, if fractions have the same denominator, to divide we just divide the numerators.

But what if fractions have different denominators?

Then, we could get a common denominator, and divide the numerators, as follows:

$\textstyle {{a \over b}\div {c \over d}={ad \over bd}\div {bc \over bd}={ad \over bc}.}$

But this takes too long. Instead, we learn the rule "invert and multiply," which gives the same answer.

$\textstyle {{a \over b}\div {c \over d}={a \over b}\times {d \over c}={ad \over bc}.}$

Here is a mathematical proof that to divide we invert and multiply.

• Theorem

$\textstyle {{a \over b}\div {c \over d}={ad \over bc}.}$

• Proof

We know that division is defined to be the inverse of multiplication. That is,

$\textstyle {m\div n=q}$

if and only if

$\textstyle {n\times q=m}.$

In the expression we want to prove, multiply the quotient by the divisor $\textstyle {{c \over d}\times {ad \over bc}={acd \over bcd}}$ which reduces to $\textstyle {a \over b}$.

Therefore,

$\textstyle {{a \over b}\div {c \over d}={ad \over bc}.}$

Another way to understand this is the following:

Question, does

$\textstyle {{\frac {a}{b}}\div {\frac {c}{d}}={\frac {a}{b}}\times {\frac {d}{c}}}$

Given/Accepted

I. Any number divided by itself is one (e.g. $\textstyle {{\frac {d}{d}}={\frac {1}{1}}}$)

II. When a number is multiplied by one it does not change (e.g. $\textstyle {{\frac {a}{b}}\times {\frac {1}{1}}={\frac {a}{b}}\times {\frac {d}{d}}={\frac {a}{b}}}$)

III. If two fractions have common denominators, then the numerators may be divided to find the quotient (e.g. $\textstyle {{\frac {ad}{bd}}\div {\frac {bc}{bd}}=ad\div bc}$)

Proof

1. $\textstyle {{\frac {a}{b}}\div {\frac {c}{d}}}$, Problem

2. $\textstyle {{\frac {ad}{bd}}\div {\frac {bc}{bd}}}$, Multiplied the first fraction by $\textstyle {\frac {d}{d}}$ and the second fraction by $\textstyle {\frac {b}{b}}$, which is the same as multiplying by one, and as accepted above (I & II) does not change the value of the fraction

Note: These values of one were chosen so the fractions would have a common denominator; bd is the common denominator.

3. $\textstyle {{\frac {ad}{bd}}\div {\frac {bc}{bd}}=ad\div bc}$, From what was given in (III)

4. $\textstyle {ad\div bc={\frac {ad}{bc}}}$, Changed notation

5. $\textstyle {{\frac {ad}{bc}}={\frac {a}{b}}\times {\frac {d}{c}}}$, Can be seen

6. $\textstyle {{\frac {a}{b}}\times {\frac {d}{c}}}$, Solution

About 4,000 years ago Egyptians divided with fractions using slightly different methods. They used least common multiples with unit fractions. Their methods gave the same answer that our modern methods give.

Converting repeating decimals to fractions

Decimal numbers, while arguably more useful to work with when performing calculations, lack the same kind of precision that regular fractions (as they are explained in this article) have. Sometimes an infinite number of decimals is required to convey the same kind of precision. Thus, it is often useful to convert repeating decimals into fractions.

For repeating patterns where the repeating pattern begins immediately after the decimal point, a simple division of the pattern by the same number of nines as numbers it has will suffice. For example (the pattern is highlighted in bold):

0.555555555555… = 5/9

0.626262626262… = 62/99

0.264264264264… = 264/999

0.629162916291… = 6291/9999

In case zeros precede the pattern, the nines are suffixed by the same number of zeros:

0.0555… = 5/90

0.000392392392… = 392/999000

0.00121212… = 12/9900

In case a non-repeating set of decimals precede the pattern (such as 0.1523987987987…), we must equate it as the sum of the non-repeating and repeating parts:

0.1523 + 0.0000987987987…

Then, convert both of these to fractions. Since the first part is not repeating, it is not converted according to the pattern given above:

1523/10000 + 987/9990000

We add these fractions by expressing both with a common divisor...

1521477/9990000 + 987/9990000

And add them.

1522464/9990000

Finally, we simplify it:

31718/208125

Rationalization

Rationalization of a fraction is a technique of estimation which has found later use in working with complex numbers. A fraction may need to be rationalized if the denominator contains any irrational numbers, imaginary numbers or complex numbers. The process of rationalization involves multiplying the top and the bottom of a fraction by its conjugate so that the denominator becomes a rational number. Even if this process results in the numerator being irrational or complex, the process may still facilitate algebra by reducing the number of irrationals one has to work with or putting the expression into a + bi form.

Special cases

A unit fraction is a vulgar fraction with a numerator of 1, e.g. ${\tfrac {1}{7}}$.

An Egyptian fraction is the sum of distinct unit fractions, e.g. ${\tfrac {1}{2}}+{\tfrac {1}{3}}$. This term derives from the fact that the ancient Egyptians had special symbols for 1/2, 2/3, and 3/4 that were used to reduce the size of numbers greater than 1/2 when such numbers were converted to an Egyptian fraction series. The remaining number after subtracting one of these special fractions was written using as a sum of distinct unit fractions according to the usual Egyptian fraction notation.

A dyadic fraction is a vulgar fraction in which the denominator is a power of two, e.g. ${\tfrac {1}{8}}$.

An expression that has the form of a fraction but actually represents division by or into an irrational number is sometimes called an "irrational fraction." A common example is $\textstyle {\frac {\pi }{2}}$, the radian measure of a right angle.

Rational numbers are the quotient field of integers. Rational functions are functions evaluated in the form of a fraction, where the numerator and denominator are polynomials. These rational expressions are the quotient field of the polynomials (over some integral domain).

A continued fraction is an expression such as $a_{0}+{\frac {1}{a_{1}+{\frac {1}{a_{2}+...}}}}$, where the a_i are integers. This is not an element of a quotient field.

The term partial fraction is used in algebra, when decomposing rational expressions (a fraction with an algebraic expression in the denominator). The goal is to write the rational expression as the sum of other rational expressions with denominators of lesser degree. For example, the rational expression $\textstyle {2x \over (x^{2}-1)}$ can be rewritten as the sum of two fractions: $\textstyle {1 \over (x+1)}$ and $\textstyle {1 \over (x-1)}$.

Pedagogical tools

In primary schools, fractions have been demonstrated through Cuisenaire rods. Other materials used to teach fractions to students in the U.S. include fraction bars, fraction strips, fraction circles, paper (for folding or cutting), pattern blocks and computer software.

History

The earliest known use of fractions is ca. 2800 B.C.E. as Ancient Indus Valley units of measurement. The Egyptians used Egyptian fractions ca. 1000 B.C.E. The Greeks used unit fractions and later continued fractions and followers of the Greek philosopher Pythagoras, ca. 530 B.C.E., discovered that the square root of two cannot be expressed as a fraction. In 150 B.C.E. Jain mathematicians in India wrote the "Sthananga Sutra," which contains work on the theory of numbers, arithmetical operations, operations with fractions.

In Sanskrit literature, fractions, or rational numbers were always expressed by an integer followed by a fraction. When the integer is written on a line, the fraction is placed below it and is itself written on two lines, the numerator called amsa part on the first line, the denominator called cheda “divisor” on the second below. If the fraction is written without any particular additional sign, one understands that it is added to the integer above it. If it is marked by a small circle or a cross (the shape of the “plus” sign in the West) placed on its right, one understands that it is subtracted from the integer. For example, Bhaskara I writes.

६ १ २ 
१ १ १० 
४ ५ ९

That is,

6 1 2 
1 1 1० 
4 5 9

to denote 6+1/4, 1+1/5, and 2–1/9

Al-Hassār, a Muslim mathematician from the Maghreb (North Africa) specializing in Islamic inheritance jurisprudence during the twelfth century, developed the modern symbolic mathematical notation for fractions, where the numerator and denominator are separated by a horizontal bar. This same fractional notation appears soon after in the work of Fibonacci in the thirteenth century.

In discussing the origins of decimal fractions, Dirk Jan Struik states that:

The introduction of decimal fractions as a common computational practice can be dated back to the Flemish pamphlet De Thiende, published at Leyden in 1585, together with a French translation, La Disme, by the Flemish mathematician Simon Stevin (1548-1620), then settled in the Northern Netherlands. It is true that decimal fractions were used by the Chinese many centuries before Stevin and that the Persian astronomer Al-Kāshī used both decimal and sexagesimal fractions with great ease in his Key to arithmetic (Samarkand, early fifteenth century).

While the Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the fifteenth century, J. Lennart Berggrenn notes that he was mistaken, as decimal fractions were first used five centuries before him by the Baghdadi mathematician Abu'l-Hasan al-Uqlidisi as early as the tenth century.

See also

• Decimal
• Number

References

ISBN links support NWE through referral fees

• Berggren, J. Lennart. "Mathematics in Medieval Islam," in Victor J Katz, and Annette Imhausen (eds.) The mathematics of Egypt, Mesopotamia, China, India, and Islam : a sourcebook. Princeton, NJ: Princeton University Press, 2007. ISBN 978-0691114859.
• Gellert, W. The VNR Concise Encyclopedia of Mathematics. New York, NY: Van Nostrand Reinhold Co., 1977. ISBN ‎ 978-0442205904.
• Luckey, P. Die Rechenkunst bei Ğamšīd b. Mas'ūd al-Kāšī. Wiesbaden, DE: Steiner, 1951.
• Struik, D.J. A Source Book in Mathematics 1200-1800. Princeton, NJ: Princeton University Press, 1986. ISBN 0691023972.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Fraction (mathematics)  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Fraction (mathematics)"

Note: Some restrictions may apply to use of individual images which are separately licensed.