Ellipse
In mathematics, an ellipse (from the Greek word ἔλλειψις, which literally means "absence") is a closed curve on a plane, such that the sum of the distances from any point on the curve to two fixed points is a constant. The two fixed points are called foci (plural of focus). A circle is a special case of an ellipse, in which the two foci coincide.
An ellipse is a type of conic section. If a conical surface is cut with a plane that does not intersect the base of the cone, the intersection of the cone and the plane is an ellipse.
The orbits of planets and many comets have been found to be elliptical.
Definitions of terms and properties
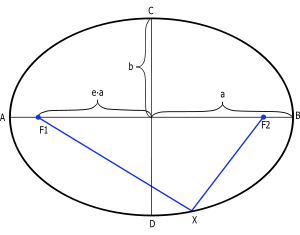
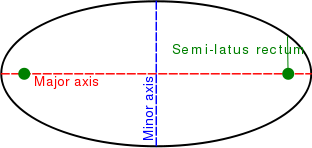
The point that lies halfway between the two foci is called the center of the ellipse. The line segment (or chord) AB (in the figure), which passes through the foci (F1, F2) and terminates on the ellipse, is called the major axis. This axis is the longest segment that can be obtained by joining two points on the ellipse. The two points at which the major axis intersects the curve are called the vertices. The line segment (chord) CD, which passes through the center, is perpendicular to the major axis, and terminates on the ellipse, is called the minor axis.
The semimajor axis (denoted by a in the figure) is one-half of the major axis and corresponds to the line segment from the center, through a focus, and to the edge of the ellipse. Likewise, the semiminor axis (denoted by b in the figure) is one-half the minor axis.
A chord drawn through a focus perpendicular to the major axis is called the latus rectum.
The area enclosed by an ellipse is πab, where a and b are the semimajor and semiminor axes.
Drawing an ellipse
An ellipse can be drawn on a sheet of paper using two pins, a pencil, and a loop of string. The pins are placed vertically at two separate points (which will become the foci of the ellipse), and the loop of string is placed around the pins and the pencil. The pencil is held vertically such that the string is taut and forms a triangle. If the pencil is moved around so that the string stays taut, it will trace out an ellipse, because the sum of the distances from the pencil to the pins will remain a constant.
Eccentricity
The shape of an ellipse can be expressed by a number called the eccentricity of the ellipse, conventionally denoted . It is the ratio obtained when the distance from the center to a focus is divided by the distance from the center to one of the vertices. Thus, eccentricity is a non-negative number less than one and greater than or equal to zero. An eccentricity of zero implies that the two foci occupy the same point (corresponding to the center), and in such a case, the ellipse is a circle.
For an ellipse with semimajor axis a and semiminor axis b, the eccentricity is
- .
The greater the eccentricity is, the larger the ratio of a to b, and therefore the more elongated the ellipse.
If c equals the distance from the center to either focus, then
- .
The distance c is known as the linear eccentricity of the ellipse. The distance between the foci is 2aε.
Ellipses in physics
In the seventeenth century, Johannes Kepler explained that the orbits along which the planets travel around the Sun are ellipses in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.
More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. Interestingly, the orbit of either body in the reference frame of the other is also an ellipse, with the other body at one focus.
The general solution for a harmonic oscillator in two or more dimensions is also an ellipse, but this time with the origin of the force located at the center of the ellipse.
Stretching and projection
An ellipse may be uniformly stretched along any axis, in or out of the plane of the ellipse, and it will still be an ellipse. The stretched ellipse will have different properties (perhaps changed eccentricity and semi-major axis length, for instance), but it will still be an ellipse (or a degenerate ellipse: a circle or a line). Similarly, any oblique projection onto a plane results in a conic section. If the projection is a closed curve on the plane, then the curve is an ellipse or a degenerate ellipse.
An ellipse can be produced by multiplying the x coordinates of all points on a circle by a constant, without changing the y coordinates. This is equivalent to stretching the circle out in the x-direction.
Reflection property
Assume an elliptic mirror with a light source at one of the foci. Then all rays are reflected to a single point—the second focus. Since no other curve has such a property, it can be used as an alternative definition of an ellipse. In a circle, all light would be reflected back to the center since all tangents are orthogonal to the radius.
Sound waves are reflected in a similar way, so in a large elliptical room a person standing at one focus can hear a person standing at another focus remarkably well. Such a room is called a whisper chamber. Examples are the National Statuary Hall Collection at the U.S. Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters), at an exhibit on sound at the Museum of Science and Industry in Chicago, in front of the University of Illinois at Urbana-Champaign Foellinger Auditorium, and also at a side chamber of the Palace of Charles V, in the Alhambra.
Equations
Algebraically, an ellipse is a curve in the Cartesian plane defined by an equation of the form
such that , where all of the coefficients are real, and where more than one solution, defining a pair of points (x, y) on the ellipse, exists.
Cartesian coordinates
An ellipse with a semimajor axis a and semiminor axis b, centered at the point and having its major axis parallel to the x-axis may be specified by the equation
- .
Parametric
This ellipse can be expressed parametrically as
where may be restricted to the interval .
Polar coordinates
If = 0 and = 0 (i.e., if the center is the origin (0,0)), then we can express this ellipse in polar coordinates by the equation
where is the eccentricity of the ellipse.
With one focus at the origin, the ellipse's polar equation is
- .
Circumference
The circumference of an ellipse is , where the function E is the complete elliptic integral of the second kind.
Semi-latus rectum and polar coordinates
The semi-latus rectum of an ellipse, usually denoted (lowercase L), is the distance from a focus of the ellipse to the ellipse itself, measured along a line perpendicular to the major axis. It is related to and (the ellipse's semi-axes) by the formula or, if using the eccentricity, .
In polar coordinates, an ellipse with one focus at the origin and the other on the negative x-axis is given by the equation
An ellipse can also be thought of as a projection of a circle: a circle on a plane at angle φ to the horizontal projected vertically onto a horizontal plane gives an ellipse of eccentricity sin φ, provided φ is not 90°.
See also
ReferencesISBN links support NWE through referral fees
- Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240
- Research and Education Association. 1999. Math Made Nice-n-Easy Books #7: Trigonometric Identities & Equations, Straight Lines, Conic Sections. Piscataway, N.J.: Research & Education Association. ISBN 0878912061
- Smith, Karen E. 2000. An Invitation to Algebraic Geometry. New York: Springer. ISBN 0387989803
- Stillwell, John. 1998. Numbers and Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387982892
External links
All links retrieved September 12, 2017.
- Ellipse on MathWorld
- Kimberling, Clark. The Shape and History of The Ellipse in Washington, D.C.
- Collection of animated ellipse demonstrations Ellipse, axes, semi-axes, area, perimeter, tangent, foci.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.