Triangle

A triangle.

A triangle is one of the basic shapes of geometry: a polygon with three corners (or vertices) and three sides (or edges) that are straight line segments.

In Euclidean geometry any three non-collinear points determine a triangle and a unique plane, that is, two-dimensional Cartesian space.

Types of triangles

Triangles can be classified according to the relative lengths of their sides:

• In an equilateral triangle, all sides are of equal length. An equilateral triangle is also an equiangular polygon, i.e. all its internal angles are equal—namely, 60°; it is a regular polygon
• In an isosceles triangle, two sides are of equal length. An isosceles triangle also has two congruent angles (namely, the angles opposite the congruent sides). An equilateral triangle is an isosceles triangle, but not all isosceles triangles are equilateral triangles.
• In a scalene triangle, all sides have different lengths. The internal angles in a scalene triangle are all different.

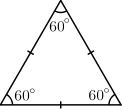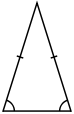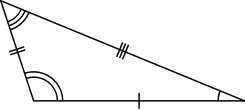Equilateral	Isosceles	Scalene

Triangles can also be classified according to the their internal angles, described below using degrees of arc.

• A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one 90° internal angle (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle. The other two sides are the legs or catheti (singular: cathetus) of the triangle.
• An obtuse triangle has one internal angle larger than 90° (an obtuse angle).
• An acute triangle has internal angles that are all smaller than 90° (three acute angles). An equilateral triangle is an acute triangle, but not all acute triangles are equilateral triangles.
• An oblique triangle has only angles that are smaller or larger than 90°. It is therefore any triangle that is not a right triangle.

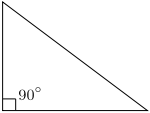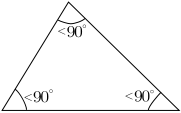Right	Obtuse	Acute
	$\underbrace {\qquad \qquad \qquad \qquad \qquad \qquad } _{}$
	Oblique

Basic facts

Elementary facts about triangles were presented by Euclid in books 1-4 of his Elements around 300 B.C.E. A triangle is a polygon and a 2-simplex (see polytope). All triangles are two-dimensional.

The angles of a triangle add up to 180 degrees. An exterior angle of a triangle (an angle that is adjacent and supplementary to an internal angle) is always equal to the two angles of a triangle that it is not adjacent/supplementary to. Like all convex polygons, the exterior angles of a triangle add up to 360 degrees.

The sum of the lengths of any two sides of a triangle always exceeds the length of the third side. That is the triangle inequality.

Two triangles are said to be similar if and only if the angles of one are equal to the corresponding angles of the other. In this case, the lengths of their corresponding sides are proportional. This occurs for example when two triangles share an angle and the sides opposite to that angle are parallel.

A few basic postulates and theorems about similar triangles:

• Two triangles are similar if at least 2 corresponding angles are congruent.
• If two corresponding sides of two triangles are in proportion, and their included angles are congruent, the triangles are similar.
• If three sides of two triangles are in proportion, the triangles are similar.

For two triangles to be congruent, each of their corresponding angles and sides must be congruent (6 total). A few basic postulates and theorems about congruent triangles:

• SAS Postulate: If two sides and the included angles of two triangles are correspondingly congruent, the two triangles are congruent.
• SSS Postulate: If every side of two triangles are correspondingly congruent, the triangles are congruent.
• ASA Postulate: If two angles and the included sides of two triangles are correspondingly congruent, the two triangles are congruent.
• AAS Theorem: If two angles and any side of two triangles are correspondingly congruent, the two triangles are congruent.
• Hypotenuse-Leg Theorem: If the hypotenuses and one pair of legs of two right triangles are correspondingly congruent, the triangles are congruent.

Using right triangles and the concept of similarity, the trigonometric functions sine and cosine can be defined. These are functions of an angle which are investigated in trigonometry.

In Euclidean geometry, the sum of the internal angles of a triangle is equal to 180°. This allows determination of the third angle of any triangle as soon as two angles are known.

The Pythagorean theorem

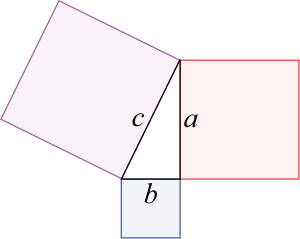
A central theorem is the Pythagorean theorem, which states in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. If the hypotenuse has length c, and the legs have lengths a and b, then the theorem states that

$a^{2}+b^{2}=c^{2}\,$

The converse is true: if the lengths of the sides of a triangle satisfy the above equation, then the triangle is a right triangle.

Some other facts about right triangles:

• The acute angles of a right triangle are complementary.
• If the legs of a right triangle are congruent, then the angles opposite the legs are congruent, acute and complementary, and thus are both 45 degrees. By the Pythagorean theorem, the length of the hypotenuse is the square root of two times the length of a leg.
• In a 30-60 right triangle, in which the acute angles measure 30 and 60 degrees, the hypotenuse is twice the length of the shorter side.

For all triangles, angles and sides are related by the law of cosines and law of sines.

Points, lines and circles associated with a triangle

There are hundreds of different constructions that find a special point inside a triangle, satisfying some unique property: see the references section for a catalogue of them. Often they are constructed by finding three lines associated in a symmetrical way with the three sides (or vertices) and then proving that the three lines meet in a single point: an important tool for proving the existence of these is Ceva's theorem, which gives a criterion for determining when three such lines are concurrent. Similarly, lines associated with a triangle are often constructed by proving that three symmetrically constructed points are collinear: here Menelaus' theorem gives a useful general criterion. In this section just a few of the most commonly-encountered constructions are explained.

The circumcenter is the center of a circle passing through the three vertices of the triangle.

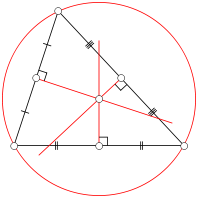
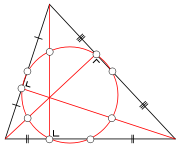
A perpendicular bisector of a triangle is a straight line passing through the midpoint of a side and being perpendicular to it (i.e. forming a right angle with it). The three perpendicular bisectors meet in a single point, the triangle's circumcenter; this point is the center of the circumcircle, the circle passing through all three vertices. The diameter of this circle can be found from the law of sines stated above.

Thales' theorem implies that if the circumcenter is located on one side of the triangle, then the opposite angle is a right one. More is true: if the circumcenter is located inside the triangle, then the triangle is acute; if the circumcenter is located outside the triangle, then the triangle is obtuse.

The intersection of the altitudes is the orthocenter.

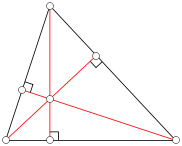
An altitude of a triangle is a straight line through a vertex and perpendicular to (i.e. forming a right angle with) the opposite side. This opposite side is called the base of the altitude, and the point where the altitude intersects the base (or its extension) is called the foot of the altitude. The length of the altitude is the distance between the base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is acute. The three vertices together with the orthocenter are said to form an orthocentric system.

The intersection of the angle bisectors finds the center of the incircle.

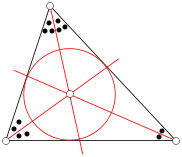
An angle bisector of a triangle is a straight line through a vertex which cuts the corresponding angle in half. The three angle bisectors intersect in a single point, the incenter, the center of the triangle's incircle. The incircle is the circle which lies inside the triangle and touches all three sides. There are three other important circles, the excircles; they lie outside the triangle and touch one side as well as the extensions of the other two. The centers of the in- and excircles form an orthocentric system.

The barycenter is the center of gravity.

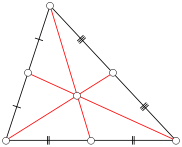
A median of a triangle is a straight line through a vertex and the midpoint of the opposite side, and divides the triangle into two equal areas. The three medians intersect in a single point, the triangle's centroid. This is also the triangle's center of gravity: if the triangle were made out of wood, say, you could balance it on its centroid, or on any line through the centroid. The centroid cuts every median in the ratio 2:1 (i.e. the distance between a vertex and the centroid is twice as large as the distance between the centroid and the midpoint of the opposite side).

Nine-point circle demonstrates a symmetry where six points lie on the edge of the triangle.

The midpoints of the three sides and the feet of the three altitudes all lie on a single circle, the triangle's nine-point circle. The remaining three points for which it is named are the midpoints of the portion of altitude between the vertices and the orthocenter. The radius of the nine-point circle is half that of the circumcircle. It touches the incircle (at the Feuerbach point) and the three excircles.

Euler's line is a straight line through the centroid (orange), orthocenter (blue), circumcenter (green) and center of the nine-point circle (red).

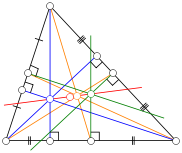
The centroid (yellow), orthocenter (blue), circumcenter (green) and barycenter of the nine-point circle (red point) all lie on a single line, known as Euler's line (red line). The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter.

The center of the incircle is not in general located on Euler's line.

If one reflects a median at the angle bisector that passes through the same vertex, one obtains a symmedian. The three symmedians intersect in a single point, the symmedian point of the triangle.

Computing the area of a triangle

Calculating the area of a triangle is an elementary problem encountered often in many different situations. The most common and simplest formula is

$S={\frac {1}{2}}bh$

where $S$ is area, $b$ is the length of the base of the triangle, and $h$ is the height or altitude of the triangle. Other approaches exist, depending on what is known about the triangle. What follows is a selection of frequently used formulae for the area of a triangle.

Using vectors

The area of a parallelogram can be calculated using vectors. Let vectors AB and AC point respectively from A to B and from A to C. The area of parallelogram ABDC is then |AB × AC|, which is the magnitude of the cross product of vectors AB and AC. |AB × AC| is equal to |h × AC|, where h represents the altitude h as a vector.

The area of triangle ABC is half of this, or S = ½|AB × AC|.

The area of triangle ABC can also be expressed in term of dot products as follows:

${\frac {1}{2}}{\sqrt {(\mathbf {AB} \cdot \mathbf {AB} )(\mathbf {AC} \cdot \mathbf {AC} )-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}={\frac {1}{2}}{\sqrt {|\mathbf {AB} |^{2}|\mathbf {AC} |^{2}-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}\,.$

Applying trigonometry to find the altitude h.

Using trigonometry

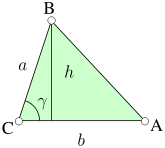
The altitude of a triangle can be found through an application of trigonometry. Using the labelling as in the image on the left, the altitude is h = a sin γ. Substituting this in the formula S = ½bh derived above, the area of the triangle can be expressed as:

$S={\frac {1}{2}}ab\sin \gamma ={\frac {1}{2}}bc\sin \alpha ={\frac {1}{2}}ca\sin \beta .$

Furthermore, since sin α = sin (π - α) = sin (β + γ), and similarly for the other two angles:

$S={\frac {1}{2}}ab\sin(\alpha +\beta )={\frac {1}{2}}bc\sin(\beta +\gamma )={\frac {1}{2}}ca\sin(\gamma +\alpha ).$

Using coordinates

If vertex A is located at the origin (0, 0) of a Cartesian coordinate system and the coordinates of the other two vertices are given by B = (x_B, y_B) and C = (x_C, y_C), then the area S can be computed as ½ times the absolute value of the determinant

$S={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{B}&x_{C}\\y_{B}&y_{C}\end{pmatrix}}\right|={\frac {1}{2}}|x_{B}y_{C}-x_{C}y_{B}|.$

For three general vertices, the equation is:

$S={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right|={\frac {1}{2}}{\big |}x_{A}y_{C}-x_{A}y_{B}+x_{B}y_{A}-x_{B}y_{C}+x_{C}y_{B}-x_{C}y_{A}{\big |}.$

In three dimensions, the area of a general triangle {A = (x_A, y_A, z_A), B = (x_B, y_B, z_B) and C = (x_C, y_C, z_C)} is the 'Pythagorean' sum of the areas of the respective projections on the three principal planes (i.e. x = 0, y = 0 and z = 0):

$S={\frac {1}{2}}{\sqrt {\left(\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right)^{2}+\left(\det {\begin{pmatrix}y_{A}&y_{B}&y_{C}\\z_{A}&z_{B}&z_{C}\\1&1&1\end{pmatrix}}\right)^{2}+\left(\det {\begin{pmatrix}z_{A}&z_{B}&z_{C}\\x_{A}&x_{B}&x_{C}\\1&1&1\end{pmatrix}}\right)^{2}}}.$

Using Heron's formula

The shape of the triangle is determined by the lengths of the sides alone. Therefore the area S also can be derived from the lengths of the sides. By Heron's formula:

$S={\sqrt {s(s-a)(s-b)(s-c)}}$

where s = ½ (a + b + c) is the semiperimeter, or half of the triangle's perimeter.

An equivalent way of writing Heron's formula is

$S={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}.$

Non-planar triangles

A non-planar triangle is a triangle which is not contained in a (flat) plane. Examples of non-planar triangles in noneuclidean geometries are spherical triangles in spherical geometry and hyperbolic triangles in hyperbolic geometry.

While all regular, planar (two dimensional) triangles contain angles that add up to 180°, there are cases in which the angles of a triangle can be greater than or less than 180°. In curved figures, a triangle on a negatively curved figure ("saddle") will have its angles add up to less than 180° while a triangle on a positively curved figure ("sphere") will have its angles add up to more than 180°. Thus, if one were to draw a giant triangle on the surface of the Earth, one would find that the sum of its angles were greater than 180°.

See also

• Angle (mathematics)
• Polygon
• Square (geometry)

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240.

• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502.

• Stillwell, John. 2005. The Four Pillars of Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387255303.

• Stillwell, John. 2006. Yearning for the Impossible: The Surprising Truths of Mathematics. Wellesley, MA: A. K. Peters. ISBN 156881254X.

• Stillwell, John. 1998. Numbers and Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387982892.

External links

All links retrieved May 2, 2023.

• Triangle Calculator - solves for remaining sides and angles when given three sides or angles, supports degrees and radians.
• Encyclopedia of triangle centers – Clark Kimberling: Lists some 3200 interesting points associated with any triangle.
• Eukleides – Christian Obrecht: Software package for creating illustrations of facts about triangles and other theorems in Euclidean geometry.
• Proof that the sum of the angles in a triangle is 180 degrees.
• Triangle definition pages – with interactive applets that are also useful in a classroom setting.
• Animated demonstrations – of triangle constructions using compass and straightedge.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Triangle  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Triangle"

Note: Some restrictions may apply to use of individual images which are separately licensed.