Hyperbola

Not to be confused with hyperbole.

Graph of a hyperbola (red). The two foci are B1 and B2. As point P moves along an arm of the hyperbola, the difference between the distances d1 and d2 remains a constant.

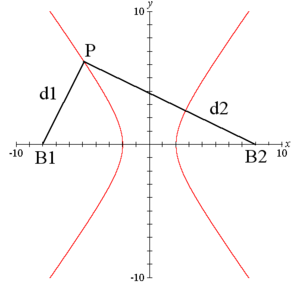
In mathematics, a hyperbola (from the Greek word ὑπερβολή, literally meaning "overshooting" or "excess") is a geometric figure such that the difference between the distances from any point on the figure to two fixed points is a constant. The two fixed points are called foci (plural of focus). This figure consists of two disconnected curves called its arms or branches that separate the foci. The bend points of the arms of a hyperbola are called the vertices (plural of vertex).

A hyperbola is a type of conic section. Thus a second definition of a hyperbola is that it is the figure obtained by the intersection between a right circular conical surface and a plane that cuts through both halves of the cone.

A third definition is that a hyperbola is the locus of points for which the ratio of the distances to one focus and to a line (called the directrix) is a constant greater than one. This constant is the eccentricity of the hyperbola.

Hyperbola (shaded green) in terms of its conic section.

Definitions of terms and properties

The point that lies halfway between the two foci is called the center of the hyperbola.

The major axis runs through the center of the hyperbola and intersects both arms at their vertices. The foci lie on the extension of the major axis of the hyperbola.

The minor axis is a straight line that runs through the center of the hyperbola and is perpendicular to the major axis.

The distance from the center of the hyperbola to the vertex of the nearest branch is known as the semi-major axis of the hyperbola.

If a point P moves along an arm of the hyperbola and the distances of that point from the two foci are called d1 and d2, the difference between d1 and d2 remains a constant. This constant is equal to two times a, where a is the semi-major axis of the hyperbola.

At large distances from the foci, the hyperbola begins to approximate two lines, known as asymptotes. The asymptotes cross at the center of the hyperbola and have slope $\pm {\frac {b}{a}}$ for an East-West opening hyperbola or $\pm {\frac {a}{b}}$ for a North-South opening hyperbola.

A hyperbola has the property that a ray originating at one of the foci is reflected in such a way as to appear to have originated at the other focus. Also, if rays are directed toward one focus from the exterior of the hyperbola, they will be reflected toward the other focus.

Special cases

Conjugate unit rectangular hyperbolas.

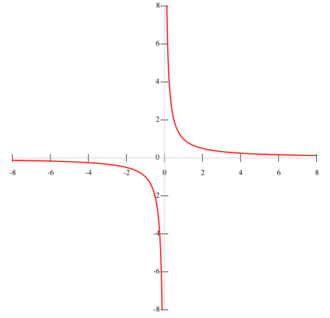
A special case of the hyperbola is the equilateral or rectangular hyperbola, in which the asymptotes intersect at right angles. The rectangular hyperbola with the coordinate axes as its asymptotes is given by the equation xy=c, where c is a constant.

Just as the sine and cosine functions give a parametric equation for the ellipse, so the hyperbolic sine and hyperbolic cosine give a parametric equation for the hyperbola.

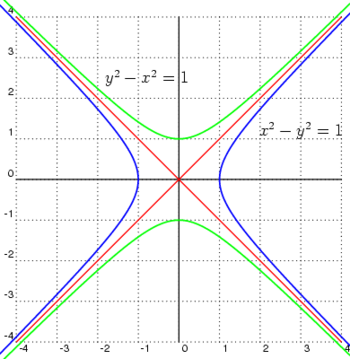
If on the hyperbola equation one switches x and y, the conjugate hyperbola is obtained. A hyperbola and its conjugate have the same asymptotes.

Equations

Algebraically, a hyperbola is a curve in the Cartesian plane defined by an equation of the form

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

such that $B^{2}>4AC$, where all of the coefficients are real, and where more than one solution, defining a pair of points (x, y) on the hyperbola, exists.

Cartesian

East-west opening hyperbola centered at (h,k):

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

North-south opening hyperbola centered at (h,k):

${\frac {\left(y-k\right)^{2}}{a^{2}}}-{\frac {\left(x-h\right)^{2}}{b^{2}}}=1$

In both formulas, a is the semi-major axis (half the distance between the two arms of the hyperbola measured along the major axis), and b is the semi-minor axis.

If one forms a rectangle with vertices on the asymptotes and two sides that are tangent to the hyperbola, the length of the sides tangent to the hyperbola are 2b in length while the sides that run parallel to the line between the foci (the major axis) are 2a in length. Note that b may be larger than a.

If one calculates the distance from any point on the hyperbola to each focus, the absolute value of the difference of those two distances is always 2a.

The eccentricity is given by

$e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$

The foci for an east-west opening hyperbola are given by

$\left(h\pm c,k\right)$ where c is given by $c^{2}=a^{2}+b^{2}$

and for a north-south opening hyperbola are given by

$\left(h,k\pm c\right)$ again with $c^{2}=a^{2}+b^{2}$

For rectangular hyperbolas with the coordinate axes parallel to their asymptotes:

$(x-h)(y-k)=c\,$

A graph of the rectangular hyperbola, $y={\tfrac {1}{x}}$.

The simplest example of these are the hyperbolas

$y={\frac {m}{x}}\,$.

Polar

East-west opening hyperbola:

$r^{2}=a\sec 2\theta \,$

North-south opening hyperbola:

$r^{2}=-a\sec 2\theta \,$

Northeast-southwest opening hyperbola:

$r^{2}=a\csc 2\theta \,$

Northwest-southeast opening hyperbola:

$r^{2}=-a\csc 2\theta \,$

In all formulas the center is at the pole, and a is the semi-major axis and semi-minor axis.

Parametric

East-west opening hyperbola:

${\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {or} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}$

North-south opening hyperbola:

${\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {or} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}$

In all formulas (h,k) is the center of the hyperbola, a is the semi-major axis, and b is the semi-minor axis.

See also

• Circle
• Conic section
• Ellipse
• Parabola

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240
• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502
• Research and Education Association. 1999. Math Made Nice-n-Easy Books #7: Trigonometric Identities & Equations, Straight Lines, Conic Sections. Piscataway, N.J.: Research & Education Association. ISBN 0878912061
• Smith, Karen E. 2000. An Invitation to Algebraic Geometry. New York: Springer. ISBN 0387989803
• Stillwell, John. 1998. Numbers and Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387982892

External links

All links retrieved January 23, 2018.

• Mathworld - Hyperbola

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Hyperbola  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Hyperbola"

Note: Some restrictions may apply to use of individual images which are separately licensed.