Distance

This article is about distance in the mathematical or physical sense.

Distance is a numerical description of the separation between objects or points at a given moment in time. In physics or everyday discussion, distance may refer to a physical length or period of time. Occasionally, it is expressed in approximate units, such as "two counties over." In mathematics, however, distance must meet rigorous criteria. In most cases, the expression "distance from A to B" is interchangeable with "distance between A and B."

Distances can be measured by various techniques. Accurate distance measurements are important for various fields of work, such as surveying, aircraft navigation, and astronomy.

Distance, length, and displacement

Distance along a path compared with displacement.

It is important to clarify how the terms length and displacement are related to distance, and how they differ. The term length usually refers to the longest (or longer) dimension of an object (or area or system), measured as the distance between two ends or sides of the object. Thus, length is generally restricted to a given object's spatial dimensions, whereas distance often refers to the extent of separation between objects (or systems).

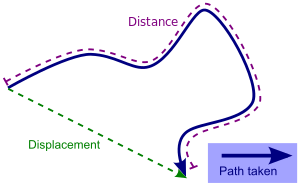
If a person, animal, vehicle, or some object travels from point A to point B, the shortest distance between A and B is known as displacement, but the distance covered may be much greater than the displacement. If points A and B coincide, the displacement is zero, but the distance covered is not. Moreover, displacement is a vector quantity, containing both magnitude and direction. By contrast, distance is a scalar quantity, expressing only magnitude. Thus, distance cannot be a negative number.

Units of distance

In the physical sciences and engineering, units of distance are the same as units of length. These units may be based on lengths of human body parts, the distance traveled in a certain number of paces, the distance between landmarks or places on the Earth, or the length of some arbitrarily chosen object.

In the International System of Units (SI), the basic unit of length is the meter, which is now defined in terms of the speed of light. The centimeter and the kilometer, derived from the meter, are also commonly used units. In U.S. customary units, English or Imperial system of units, units of length in common usage are the inch, the foot, the yard, and the mile.

Units used to denote distances in the vastness of space, as in astronomy, are much longer than those typically used on Earth. They include the astronomical unit, the light-year, and the parsec.

To define microscopically small distances, as in chemistry and microbiology, units used include the micron (or micrometer) and the ångström.

Measurement of distance

Various techniques have been developed for the measurement of length or distance. For fairly short lengths and distances, a person may use a ruler or measuring tape. For longer distances traveled by a vehicle, the odometer is useful. Some methods rely on a mathematical approach known as triangulation, which is based on geometric relationships. Various highly sensitive and precise techniques involve the use of lasers. Some laser distance meters measure the "time of flight" of a laser pulse, that is, the time it takes for a laser pulse to travel round-trip between a laser emitter and a target. Advanced laser techniques have been used to find the distance of the Moon from the Earth at an accuracy of a few centimeters.

Accurate distance measurements are important for people working in various fields, such as surveying, aircraft navigation, and astronomy. These areas are discussed briefly below.

Surveying

Surveyor at work with a leveling instrument.

Surveying is the technique and science of accurately determining the terrestrial or three-dimensional space position of points and the distances and angles between them. These points are usually, but not exclusively, associated with positions on the surface of the Earth. An alternative definition, given by the American Congress on Surveying and Mapping (ACSM), states that surveying is the science and art of making all essential measurements to determine the relative position of points and/or physical and cultural details above, on, or beneath the surface of the Earth, and to depict them in a usable form, or to establish the position of points and/or details.

Surveying has been an essential element in the development of the human environment since the beginning of recorded history (about 5000 years ago), and it is a requirement in the planning and execution of nearly every form of construction. Its most familiar modern uses are in the fields of transport, building and construction, communications, mapping, and in defining legal boundaries for land ownership. To accomplish their objective, surveyors use elements of geometry, engineering, trigonometry, mathematics, physics, and law.

Aircraft navigation

Distance measuring equipment (DME) at an airport.

Distance Measuring Equipment (DME) is a transponder-based radio navigation technology that measures distance by timing the propagation delay of VHF or UHF radio signals. Aircraft pilots use DME to determine their distance from a land-based transponder by sending and receiving pulse pairs—two pulses of fixed duration and separation.

The DME system is composed of a UHF transmitter/receiver (interrogator) in the aircraft and a UHF receiver/transmitter (transponder) on the ground. The aircraft interrogates the ground transponder with a series of pulse-pairs (interrogations), and the ground station replies with an identical sequence of reply pulse-pairs with a precise time delay (typically 50 microseconds). The DME receiver in the aircraft searches for pulse-pairs with the correct time interval between them. The aircraft interrogator locks on to the DME ground station once it understands that the particular pulse sequence is the interrogation sequence it sent out originally.

A radio pulse takes around 12.36 microseconds to travel one nautical mile to and from, this is also referred to as a radar-mile. The time difference between interrogation and reply minus the 50 microsecond ground transponder delay is measured by the interrogator's timing circuitry and translated into a distance measurement in nautical miles which is then displayed in the cockpit.

Astronomy

Extragalactic distance ladder.

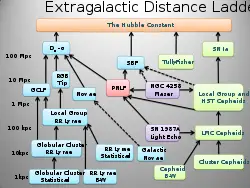
The cosmic distance ladder (also known as the Extragalactic Distance Scale) is the succession of methods by which astronomers determine distances to celestial objects. A direct distance measurement to an astronomical object is only possible for objects that are "close enough" (within about a thousand parsecs) to Earth. The techniques for determining distances to more distant objects are all based on various measured correlations between methods that work at close distances with methods that work at larger distances. The ladder analogy arises because no one technique can measure distances at all ranges encountered in astronomy. Instead, one method can be used to measure nearby distances, a second can be used to measure nearby-to-intermediate distances, and so on. Each rung of the ladder provides information that can be used to determine distances at the next higher rung.

At the base of the ladder are fundamental distance measurements, in which distances are determined directly, with no physical assumptions about the nature of the object in question. These direct methods are:

• parallax (or triangulation) based upon trigonometry, using precise measurements of angles, similar to what is used in surveying.
• light travel time (that is, the constancy of the speed of light), as in radar. Radar can (for practical reasons) only be used within the Solar System.

Beyond the use of parallax, the overlapping chain of distance measurement techniques includes the use of cepheid variables, planetary nebulae, most luminous supergiants, most luminous globular clusters, most luminous HII regions, supernovae, and Hubble constant and red shifts.

Mathematics

Geometry

In neutral geometry, the minimum distance between two points is the length of the line segment between them.

In analytic geometry, one can find the distance between two points of the xy-plane using the distance formula. The distance between (x₁, y₁) and (x₂, y₂) is given by

$d={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}}}={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.\,$

Similarly, given points (x₁, y₁, z₁) and (x₂, y₂, z₂) in three-space, the distance between them is

$d={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}}}={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}}}.$

Which is easily proven by constructing a right triangle with a leg on the hypotenuse of another (with the other leg orthogonal to the plane that contains the first triangle) and applying the Pythagorean theorem.

In the study of complicated geometries, we call this (most common) type of distance Euclidean distance, as it is derived from the Pythagorean theorem, which does not hold in Non-Euclidean geometries. This distance formula can also be expanded into the arc-length formula.

In pseudo code the common distance formula is written like this:

square_root( power(x2-x1, 2) + power(y2-y1, 2) );

Distance in Euclidean space

In the Euclidean space Rⁿ, the distance between two points is usually given by the Euclidean distance (2-norm distance). Other distances, based on other norms, are sometimes used instead.

For a point (x₁, x₂, ...,x_n) and a point (y₁, y₂, ...,y_n), the Minkowski distance of order p (p-norm distance) is defined as:

1-norm distance	$=\sum _{i=1}^{n}\left|x_{i}-y_{i}\right|$
2-norm distance	$=\left(\sum _{i=1}^{n}\left|x_{i}-y_{i}\right|^{2}\right)^{1/2}$
p-norm distance	$=\left(\sum _{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{1/p}$
infinity norm distance	$=\lim _{p\to \infty }\left(\sum _{i=1}^{n}\left|x_{i}-y_{i}\right|^{p}\right)^{1/p}$
	$=\max \left(|x_{1}-y_{1}|,|x_{2}-y_{2}|,\ldots ,|x_{n}-y_{n}|\right).$

p need not be an integer, but it cannot be less than 1, because otherwise the triangle inequality does not hold.

The 2-norm distance is the Euclidean distance, a generalization of the Pythagorean theorem to more than two coordinates. It is what would be obtained if the distance between two points were measured with a ruler: the "intuitive" idea of distance.

The 1-norm distance is more colorfully called the taxicab norm or Manhattan distance, because it is the distance a car would drive in a city laid out in square blocks (if there are no one-way streets).

The infinity norm distance is also called Chebyshev distance. In 2D it represents the distance kings must travel between two squares on a chessboard.

The p-norm is rarely used for values of p other than 1, 2, and infinity, but see super ellipse.

In physical space the Euclidean distance is in a way the most natural one, because in this case the length of a rigid body does not change with rotation.

General case

In mathematics, in particular geometry, a distance function on a given set M is a function d: M×M → R, where R denotes the set of real numbers, that satisfies the following conditions:

• d(x,y) ≥ 0, and d(x,y) = 0 if and only if x = y. (Distance is positive between two different points, and is zero precisely from a point to itself.)
• It is symmetric: d(x,y) = d(y,x). (The distance between x and y is the same in either direction.)
• It satisfies the triangle inequality: d(x,z) ≤ d(x,y) + d(y,z). (The distance between two points is the shortest distance along any path).

Such a distance function is known as a metric. Together with the set, it makes up a metric space.

For example, the usual definition of distance between two real numbers x and y is: d(x,y) = |x − y|. This definition satisfies the three conditions above, and corresponds to the standard topology of the real line. But distance on a given set is a definitional choice. Another possible choice is to define: d(x,y) = 0 if x = y, and 1 otherwise. This also defines a metric, but gives a completely different topology, the "discrete topology"; with this definition numbers cannot be arbitrarily close.

Distances between sets and between a point and a set

Various distance definitions are possible between objects. For example, between celestial bodies one should not confuse the surface-to-surface distance and the center-to-center distance. If the former is much less than the latter, as for a LEO, the first tends to be quoted (altitude), otherwise, e.g. for the Earth-Moon distance, the latter.

There are two common definitions for the distance between two non-empty subsets of a given set:

• One version of distance between two non-empty sets is the infimum of the distances between any two of their respective points, which is the every-day meaning of the word. This is a symmetric prametric. On a collection of sets of which some touch or overlap each other, it is not "separating," because the distance between two different but touching or overlapping sets is zero. Also it is not hemimetric, i.e., the triangle inequality does not hold, except in special cases. Therefore only in special cases this distance makes a collection of sets a metric space.
• The Hausdorff distance is the larger of two values, one being the supremum, for a point ranging over one set, of the infimum, for a second point ranging over the other set, of the distance between the points, and the other value being likewise defined but with the roles of the two sets swapped. This distance makes the set of non-empty compact subsets of a metric space itself a metric space.

The distance between a point and a sethttps://www.newworldencyclopedia.org/entry/Metric_space#Distance_between_points_and_sets is the infimum of the distances between the point and those in the set. This corresponds to the distance, according to the first-mentioned definition above of the distance between sets, from the set containing only this point to the other set.

In terms of this, the definition of the Hausdorff distance can be simplified: it is the larger of two values, one being the supremum, for a point ranging over one set, of the distance between the point and the set, and the other value being likewise defined but with the roles of the two sets swapped.

Other "distances"

• Mahalanobis distance is used in statistics.
• Hamming distance is used in coding theory.
• Levenshtein distance
• Chebyshev distance

References

ISBN links support NWE through referral fees

• Abdi, Hervé. Distance Encyclopedia of Measurement and Statistics. Neil Salkind, ed. Thousand Oaks, CA: Sage, 2007. Retrieved July 23, 2020.
• Deza, Elena, and Michel Marie Deza. Dictionary of Distances. Amsterdam, The Netherlands: Elsevier, 2006. ISBN 978-0444520876
• Figliola, R. S., and Donald E. Beasley. Theory and Design for Mechanical Measurements, 4th ed. Hoboken, NJ: John Wiley, 2006. ISBN 978-0471445937
• Webb, Stephen. Measuring the Universe: The Cosmological Distance Ladder. Springer-Praxis Series in Astronomy and Astrophysics. London: Springer, 1999. ISBN 1852331062

External links

All links retrieved January 29, 2024.

• How To Measure Any Distance With The Pythagorean Theorem.
• Distance Measurements with Lasers Encyclopedia of Laser Physics and Technology.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Distance  ^history
• Distance_measuring_equipment  ^history
• Cosmic_distance_ladder  ^history
• Surveying  ^history
• Length  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Distance"

Note: Some restrictions may apply to use of individual images which are separately licensed.