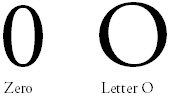- This page is about the number and digit 0 or "zero."
|
List of numbers ‚ÄĒ Integers | |
| Cardinal | 0 zero o/oh nought naught nil |
| Ordinal | 0th zeroth |
| Factorization | |
| Divisors | N/A |
| Roman numeral | N/A |
| Binary | 0 |
| Octal | 0 |
| Duodecimal | 0 |
| Hexadecimal | 0 |
0 (zero) is both a number and a numerical digit used to represent that number in numerals. As a number, zero means nothing‚ÄĒan absence of other values. It plays a central role in mathematics as the identity element of the integers, real numbers, and many other algebraic structures. As a digit, zero is used as a placeholder in place value systems. Historically, it was the last digit to come into use. In the English language, zero may also be called nil when a number, o/oh when a numeral, and nought/naught in either context.
0 as a number
0 is the integer that precedes the positive 1, and follows ‚ąí1. In most (if not all) numerical systems, 0 was identified before the idea of 'negative integers' was accepted.
Zero is an integer which quantifies a count or an amount of null size; that is, if the number of your brothers is zero, that means the same thing as having no brothers, and if something has a weight of zero, it has no weight. If the difference between the number of pieces in two piles is zero, it means the two piles have an equal number of pieces. Before counting starts, the result can be assumed to be zero; that is the number of items counted before you count the first item and counting the first item brings the result to one. And if there are no items to be counted, zero remains the final result.
While mathematicians all accept zero as a number, some non-mathematicians would say that zero is not a number, arguing one cannot have zero of something. Others hold that if you have a bank balance of zero, you have a specific quantity of money in your account, namely none. It is that latter view which is accepted by mathematicians and most others.
Almost all historians omit the year zero from the proleptic Gregorian and Julian calendars, but astronomers include it in these same calendars. However, the phrase Year Zero may be used to describe any event considered so significant that it virtually starts a new time reckoning.
0 as a numeral
The modern numeral 0 is normally written as a circle or (rounded) rectangle. In old-style fonts with text figures, 0 is usually the same height as a lowercase x.
On the seven-segment displays of calculators, watches, etc., 0 is usually written with six line segments, though on some historical calculator models it was written with four line segments. This variant glyph has not caught on.
It is important to distinguish the number zero (as in the "zero brothers" example above) from the numeral or digit zero, used in numeral systems using positional notation. Successive positions of digits have higher values, so the digit zero is used to skip a position and give appropriate value to the preceding and following digits. A zero digit is not always necessary in a positional number system: bijective numeration provides a possible counterexample.
Etymology
The word zero comes through the Arabic literal translation of the Sanskrit ŇõŇęnya ( ŗ§∂ŗ•āŗ§®ŗ•ćŗ§Į ), meaning void or empty, into ŠĻ£ifr (ōĶŔĀōĪ) meaning empty or vacant. Through transliteration this became zephyr or zephyrus in Latin. The word zephyrus already meant "west wind" in Latin; the proper noun Zephyrus was the Roman god of the west wind (after the Greek god Zephyros). With its new use for the concept of zero, zephyr came to mean a light breeze‚ÄĒ"an almost nothing."[1] This became zefiro in Italian, which was contracted to zero in Venetian, giving the modern English word.
As the Hindu decimal zero and its new mathematics spread from the Arab world to Europe in the Middle Ages, words derived from sifr and zephyrus came to refer to calculation, as well as to privileged knowledge and secret codes. According to Ifrah, "in thirteenth-century Paris, a 'worthless fellow' was called a… cifre en algorisme, i.e., an 'arithmetical nothing.'"[1] The Arabic root gave rise to the modern French chiffre, which means digit, figure, or number; chiffrer, to calculate or compute; and chiffré, encrypted; as well as to the English word cipher. Below are some more examples:
- Arabic: Sifr
- Czech/Slovak: cifra, digit; Ň°ifra, cypher
- Danish: ciffer, digit
- Dutch: cijfer, digit
- French: zéro, zero
- German: Ziffer, digit, figure, numeral, cypher
- Hindi: shunya
- Hungarian: nulla
- Italian: cifra, digit, numeral, cypher; zero, zero
- Kannada: sonne
- Norwegian: siffer, digit, numeral, cypher; null, zero
- Persian: Sefr
- Polish: cyfra, digit; szyfrowańá, to encrypt; zero, zero
- Portuguese: cifra, figure, numeral, cypher, code; zero, zero
- Russian: —Ü–ł—Ą—Ä–į (tsifra), digit, numeral; —ą–ł—Ą—Ä (shifr) cypher, code
- Slovenian: cifra, digit
- Spanish: cifra, figure, numeral, cypher, code; cero, zero
- Swedish: siffra, numeral, sum, digit; chiffer, cypher
- Serbian: —Ü–ł—Ą—Ä–į (tsifra), digit, numeral; —ą–ł—Ą—Ä–į (shifra) cypher, code; –Ĺ—É–Ľ–į (nula), zero
- Turkish: SńĪfńĪr
- Urdu: Sifer, Anda, Zero
Note that zero in Greek is translated as őúő∑őīő≠őĹ (M√®den).
History
Early history of zero
By the mid-second millennium B.C.E., the Babylonians had a sophisticated sexagesimal (base-60) positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. By 300 B.C.E. a punctuation symbol (two slanted wedges) was co-opted as a placeholder in the same Babylonian system. In a tablet unearthed at Kish (dating from perhaps as far back as 700 B.C.E.), the scribe B√™l-b√Ęn-aplu wrote his zeroes with three hooks, rather than two slanted wedges.[2]
The Babylonian placeholder was not a true zero because it was not used alone. Nor was it used at the end of a number. Thus numbers like 2 and 120 (2√ó60), 3 and 180 (3√ó60), 4 and 240 (4√ó60), etc. looked the same because the larger numbers lacked a final sexagesimal placeholder. Only context could differentiate them.
Records show that the ancient Greeks seemed unsure about the status of zero as a number: they asked themselves "How can nothing be something?," leading to interesting philosophical and, by the Medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero. (The ancient Greeks even questioned that 1 was a number.)
Early use of something like zero by the Indian scholar Pingala (circa 5th-2nd century B.C.E.), implied at first glance by his use of binary numbers, is only the modern binary representation using 0 and 1 applied to Pingala's binary system, which used short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code.[3][4] Nevertheless, he and other Indian scholars at the time used the Sanskrit word ŇõŇęnya (the origin of the word zero after a series of transliterations and a literal translation) to refer to zero or void.[5]

This is the second oldest Long Count date yet discovered. The numerals 7.16.6.16.18 translate to September 32 B.C.E. (Julian). The glyphs surrounding the date are what is thought to be one of the few surviving examples of Epi-Olmec script.
History of zero
The Long Count calendar developed in south-central Mexico required the use of zero as a place-holder within its vigesimal (base-20) positional numeral system. A shell glyph‚ÄĒ![]() ‚ÄĒwas used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 B.C.E. Since the eight earliest Long Count dates appear outside the Maya homeland,[6] it is assumed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs. Indeed, many of the earliest Long Count dates were found within the Olmec heartland, although the fact that the Olmec civilization had come to an end by the fourth century B.C.E., several centuries before the earliest known Long Count dates, argues against the zero being an Olmec invention.
‚ÄĒwas used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 B.C.E. Since the eight earliest Long Count dates appear outside the Maya homeland,[6] it is assumed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs. Indeed, many of the earliest Long Count dates were found within the Olmec heartland, although the fact that the Olmec civilization had come to an end by the fourth century B.C.E., several centuries before the earliest known Long Count dates, argues against the zero being an Olmec invention.
Although zero became an integral part of Maya numerals, it of course did not influence Old World numeral systems.
By 130 C.E., Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero (a small circle with a long overbar) within a sexagesimal numeral system otherwise using alphabetic Greek numerals. Because it was used alone, not just as a placeholder, this Hellenistic zero was perhaps the first documented use of a number zero in the Old World. However, the positions were usually limited to the fractional part of a number (called minutes, seconds, thirds, fourths, etc.)‚ÄĒthey were not used for the integral part of a number.
Another zero was used in tables alongside Roman numerals by 525 (first known use by Dionysius Exiguus), but as a word, nulla, meaning nothing, not as a symbol. When division produced zero as a remainder, nihil, also meaning nothing, was used. These medieval zeros were used by all future medieval computists (calculators of Easter). An isolated use of their initial, N, was used in a table of Roman numerals by Bede or a colleague about 725, as a zero symbol.
The oldest known text to use zero is the Jain text from India entitled the Lokavibhaaga, dated 458 C.E.[1]
The first indubitable appearance of a symbol for zero appears in 876 in India on a stone tablet in Gwalior. Documents on copper plates, with the same small o in them, dated back as far as the sixth century C.E. abound.[2]
Rules of Brahmagupta
The rules governing the use of zero appeared for the first time in the book Brahmasputha Siddhanta written in 628 by Brahmagupta (598-670). Here, Brahmagupta considers not only zero but also negative numbers, and the algebraic rules for the elementary operations of arithmetic with such numbers. In some instances, his rules differ from the modern standard. Brahamagupta's rules are given below:[7]
- The sum of two positive quantities is positive
- The sum of two negative quantities is negative
- The sum of zero and a negative number is negative
- The sum of a positive number and zero is positive
- The sum of zero and zero is zero
- The sum of a positive and a negative is their difference; or, if they are equal, zero
- In subtraction, the less is to be taken from the greater, positive from positive
- In subtraction, the less is to be taken from the greater, negative from negative
- When the greater however, is subtracted from the less, the difference is reversed
- When positive is to be subtracted from negative, and negative from positive, they must be added together
- The product of a negative quantity and a positive quantity is negative
- The product of a negative quantity and a negative quantity is positive
- The product of two positive, is positive
- Positive divided by positive or negative by negative is positive
- Positive divided by negative is negative. Negative divided by positive is negative
- A positive or negative number when divided by zero is a fraction with the zero as denominator
- Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator
- Zero divided by zero is zero
In saying "zero divided by zero is zero," Brahmagupta differs from the modern position. Mathematicians normally do not assign a value, whereas computers and calculators will sometimes assign NaN, which means "not a number." Moreover, non-zero positive or negative numbers when divided by zero are either assigned no value, or a value of unsigned infinity, positive infinity, or negative infinity. Once again, these assignments are not numbers, and are associated more with computer science than pure mathematics, where in most contexts no assignment is made. (See division by zero)
Zero as a decimal digit
Positional notation without the use of zero (using an empty space in tabular arrangements, or the word kha "emptiness") is known to have been in use in India from the sixth century. The earliest certain use of zero as a decimal positional digit dates to the ninth century. The glyph for the zero digit was written in the shape of a dot, and consequently called bindu "dot."
The Hindu-Arabic numeral system reached Europe in the eleventh century, via the Iberian Peninsula through Spanish Muslims the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac (c. 940-1003). They came to be known as "Arabic numerals." The Italian mathematician Leonardo of Pisa (c. 1170-1250), also called Fibonacci,* was instrumental in bringing the system into European mathematics in 1202. Here, Leonardo states:
There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods… But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus. (Modus Indorum)… The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 … any number may be written.[8]
Here Leonardo of Pisa uses the word sign "0," indicating it is like a sign to do operations like addition or multiplication, but he did not recognize zero as a number in its own right.
In mathematics
Elementary algebra
Zero (0) is the lowest non-negative integer. The natural number following zero is one and no natural number precedes zero. Zero may or may not be counted as a natural number, depending on the definition of natural numbers.
In set theory, the number zero is the cardinality of the empty set: if one does not have any apples, then one has zero apples. Therefore, in some cases, zero is defined to be the empty set.
Zero is neither positive nor negative, neither a prime number nor a composite number, nor is it a unit.
The following are some basic rules for dealing with the number zero. These rules apply for any complex number x, unless otherwise stated.
- Addition: x + 0 = 0 + x = x. (That is, 0 is an identity element with respect to addition.)
- Subtraction: x¬†‚ąí¬†0 = x and 0¬†‚ąí¬†x = ‚ąí x.
- Multiplication: x · 0 = 0 · x = 0.
- Division: 0 / x = 0, for nonzero x. But x / 0 is undefined, because 0 has no multiplicative inverse, a consequence of the previous rule. For positive x, as y in x / y approaches zero from positive values, its quotient increases toward positive infinity, but as y approaches zero from negative values, the quotient increases toward negative infinity. The different quotients confirms that division by zero is undefined.
- Exponentiation: x0 = 1, except that the case x = 0 may be left undefined in some contexts. For all positive real x, 0x = 0.
- The sum of 0 numbers is 0, and the product of 0 numbers is 1.
The expression "0/0" is an "indeterminate form." That does not simply mean that it is undefined; rather, it means that if f(x) and g(x) both approach 0 as x approaches some number, then f(x)/g(x) could approach any finite number or ‚ąě or ‚ąí‚ąě; it depends on which functions f and g are. See L'Hopital's rule.
Extended use of zero in mathematics
- Zero is the identity element in an additive group or the additive identity of a ring.
- A zero of a function is a point in the domain of the function whose image under the function is zero. When there are finitely many zeros these are called the roots of the function. See zero (complex analysis).
- In geometry, the dimension of a point is 0.
- The concept of "almost" impossible in probability. More generally, the concept of almost nowhere in measure theory. For instance: if one chooses a point on a unit line interval [0,1) at random, it is not impossible to choose 0.5 exactly, but the probability that you will is zero.
- A zero function (or zero map) is a constant function with 0 as its only possible output value; i.e., f(x) = 0 for all x defined. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map.
- Zero is one of three possible return values of the Möbius function. Passed an integer of the form x2 or x2y (for x > 1), the Möbius function returns zero.
- Zero is the first Perrin number.
In science
Physics
The value zero plays a special role for a large number of physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, on the Kelvin temperature scale, zero is the coldest possible temperature (negative temperatures exist but are not actually colder), whereas on the Celsius scale, zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value‚ÄĒfor example, at a value for the threshold of hearing.
Chemistry
Zero has been proposed as the atomic number of the theoretical element tetraneutronium. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in their own right. This would create an element with no protons and no charge on its nucleus.
As early as 1926 Professor Andreas von Antropoff coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements. It is at the center of the Chemical Galaxy (2005).
In computer science
Numbering from 1 or 0?
The most common practice throughout human history has been to start counting at one. Nevertheless, in computer science zero has become the standard starting point. For example, in almost all old programming languages, an array starts from 1 by default. As programming languages have developed, it has become more common that an array starts from zero by default, the "first" item in the array being item 0. In particular, the popularity of the programming language "C" in the 1980s has made this approach common.
One reason for this convention is that modular arithmetic normally describes a set of N numbers as containing 0,1,2,… N-1 in order to contain the additive identity. Because of this, many arithmetic concepts (such as hash tables) are less elegant to express in code unless the array starts at zero.
In certain cases, counting from zero improves the efficiency of various algorithms, such as in searching or sorting arrays. Improved efficiency means that the algorithm takes either less time, less resources, or both, to complete a given task.
This situation can lead to some confusion in terminology. In a zero-based indexing scheme, the first element is "element number zero"; likewise, the twelfth element is "element number eleven." Therefore, an analogy from the ordinal numbers to the quantity of objects numbered appears; the highest index of n objects will be (n-1) and referred to the n:th element. For this reason, the first element is often referred to as the zeroth element to eliminate any possible doubt.
Null value
In databases a field can have a null value. This is equivalent to the field not having a value. For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result. Asking for all records with value 0 or value not equal 0 will not yield all records, since the records with value null are excluded.
Null pointer
A null pointer is a pointer in a computer program that does not point to any object or function, which means that when it appears in a program or code, it tells the computer to take no action on the associated portion of the code.
Negative zero
In some signed number representations (but not the two's complement representation predominant today) and most floating point number representations, zero has two distinct representations, one grouping it with the positive numbers and one with the negatives; this latter representation is known as negative zero. Representations with negative zero can be troublesome, because the two zeros will compare equal but may be treated differently by some operations.
Distinguishing zero from O
The oval-shaped zero and circular letter O together came into use on modern character displays. The zero with a dot in the center seems to have originated as an option on IBM 3270 controllers (this has the problem that it looks like the Greek letter Theta). The slashed zero, looking identical to the letter O other than the slash, is used in old-style ASCII graphic sets descended from the default typewheel on the venerable ASR-33 Teletype. This format causes problems because of its similarity to the symbol ‚ąÖ, representing the empty set, as well as for certain Scandinavian languages which use √ė as a letter.
The convention which has the letter O with a slash and the zero without was used at IBM and a few other early mainframe makers; this is even more problematic for Scandinavians because it means two of their letters collide. Some Burroughs/Unisys equipment displays a zero with a reversed slash. And yet another convention common on early line printers left zero unornamented but added a tail or hook to the letter-O so that it resembled an inverted Q or cursive capital letter-O.
The typeface used on some European number plates for cars distinguish the two symbols by making the zero rather egg-shaped and the O more circular, but most of all by slitting open the zero on the upper right side, so the circle is not closed any more (as in German plates). The typeface chosen is called fälschungserschwerende Schrift (abbr.: FE Schrift), meaning "unfalsifiable script." Note that those used in the United Kingdom do not differentiate between the two as there can never be any ambiguity if the design is correctly spaced.
In paper writing one may not distinguish the 0 and O at all, or may add a slash across it in order to show the difference, although this sometimes causes ambiguity in regard to the symbol for the null set.
Quotes
The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang. It is like coining the Nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power. G. B. Halsted
…a profound and important idea which appears so simple to us now that we ignore its true merit. But its very simplicity and the great ease which it lent to all computations put our arithmetic in the first rank of useful inventions. Pierre-Simon Laplace
The point about zero is that we do not need to use it in the operations of daily life. No one goes out to buy zero fish. It is in a way the most civilized of all the cardinals, and its use is only forced on us by the needs of cultivated modes of thought. Alfred North Whitehead
‚Ķa fine and wonderful refuge of the divine spirit‚ÄĒalmost an amphibian between being and non-being. Gottfried Leibniz
In other fields
- In some countries, dialing 0 on a telephone places a call for operator assistance.
- In Braille, the numeral 0 has the same dot configuration as the letter J.
- DVDs that can be played in any region are sometimes referred to as being "region 0"
- In classical music, 0 is very rarely used as a number for a composition, the only two examples on the fringes of the standard repertoire probably being Anton Bruckner's Symphony No. 0 in D minor and Alfred Schnittke's Symphony No. 0
- In tarot, card No. 0 is the Fool
See also
- Number
- Number theory
Notes
- ‚ÜĎ 1.0 1.1 1.2 Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer (Wiley, 2000, ISBN 0471393401).
- ‚ÜĎ 2.0 2.1 Robert Kaplan and Ellen Kaplan, The Nothing That Is: A Natural History of Zero (Oxford: Oxford University Press, 2000, ISBN 978-0195142372).
- ‚ÜĎ ICA.net, Binary Numbers in Ancient India with information from scholarly article by B. van Nooten, "Binary Numbers in Indian Antiquity", Journal of Indian Studies 21 (1993): 31-50. Retrieved September 19, 2017.
- ‚ÜĎ Rachel Hall, "Math for Poets and Drummers" Saint Joseph's University, February 15, 2005. Retrieved September 19, 2017.
- ‚ÜĎ Kim Plofker, Mathematics in India (Princeton University Press, 2009, ISBN 978-0691120676).
- ‚ÜĎ Richard A. Diehl, The Olmecs: America's First Civilization (London: Thames & Hudson, 2005, ISBN 0500285039), 186.
- ‚ÜĎ Henry Thomas Colebrooke, Algebra with Arithmetic of Brahmagupta and Bhaskara (1817).
- ‚ÜĎ Laurence Sigler, Fibonacci's Liber Abaci(Springer, 2002, ISBN 978-0387954196).
ReferencesISBN links support NWE through referral fees
This article was originally based on material from the Free On-line Dictionary of Computing, which is licensed under the GNU Free Documentation License.
- Barrow, John D. The Book of Nothing. Pantheon, 2001. ISBN 0375420991
- Colebrooke, Henry Thomas. Algebra, With Arithmetic And Mensuration, From The Sanscrit Of Brahmegupta And Bhascara. Nabu Press, 2011. ISBN 978-1175467102
- Diehl, Richard A. The Olmecs: America's First Civilization. London: Thames & Hudson, 2005. ISBN 0500285039
- Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley, 2000. ISBN 0471393401
- Kaplan, Robert and Ellen Kaplan (illus). The Nothing That Is: A Natural History of Zero. Oxford University Press, 2000. ISBN 0195142373
- Plofker, Kim. Mathematics in India. Princeton University Press, 2009. ISBN 978-0691120676
- Seife, Charles. Zero: The Biography of a Dangerous Idea. Penguin USA, 2000. ISBN 0140296476
- Sigler, Laurence. Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation. Springer, 2002. ISBN 978-0387954196
External links
All links retrieved June 13, 2023.
- J. J. O'Connor and E. F. Robertson A History of Zero
- Zero in Four Dimensions: Cultural, Historical, Mathematical, and Psychological Perspectives
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.