Refraction
Refraction is the change in direction of a wave due to a change in its speed, as observed when a wave passes from one medium to another. The most common example is the refraction of light, as happens in the formation of rainbows in the sky or rainbow-like bands when white light passes through a glass prism. Other types of waves also undergo refraction, for example, when sound waves pass from one medium into another.
The refraction of waves through a medium is quantified in terms of what is called the refractive index (or index of refraction). The refractive index of a medium is a measure of how much the speed of light (or other waves) is reduced inside the medium, compared with the speed of light in vacuum or air. For example, if a sample of glass has a refractive index of 1.5, it means that the speed of light traveling through the glass is times the speed of light in vacuum or air.
Based on knowledge of the properties of refraction and refractive index, a number of applications have been developed. For example, the invention of lenses and refracting telescopes rests on an understanding of refraction. Also, knowledge of the refractive index of various substances is used to evaluate the purity of a substance or measure its concentration in a mixture. In eye tests performed by ophthalmologists or optometrists, the property of refraction forms the basis for the technique known as refractometry.
Explanation
In optics, refraction occurs when light waves travel from a medium with a particular refractive index to a second medium with another refractive index. At the boundary between the media, the wave's phase velocity is altered, it changes direction, and its wavelength increases or decreases, but its frequency remains constant. For example, a light ray will undergo refraction as it enters and leaves glass. An understanding of this concept led to the invention of lenses and the refracting telescope.
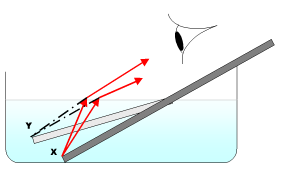
Refraction can be seen when looking into a bowl of water. Air has a refractive index of about 1.0003, and water has a refractive index of about 1.33. If a person looks at a straight object, such as a pencil or straw, which is placed at a slant, partially in the water, the object appears to bend at the water's surface. This is due to the bending of light rays as they move from the water to the air. Once the rays reach the eye, the eye traces them back as straight lines (lines of sight). The lines of sight (shown as dashed lines) intersect at a higher position than where the actual rays originated. This causes the pencil to appear higher and the water to appear shallower than it really is. The depth that the water appears to be when viewed from above is known as the apparent depth,
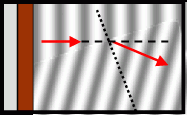
The diagram on the right shows an example of refraction in water waves. Ripples travel from the left and pass over a shallower region inclined at an angle to the wavefront. The waves travel more slowly in the shallower water, so the wavelength decreases and the wave bends at the boundary. The dotted line represents the normal to the boundary. The dashed line represents the original direction of the waves. The phenomenon explains why waves on a shoreline never hit the shoreline at an angle. Whichever direction the waves travel in deep water, they always refract towards the normal as they enter the shallower water near the beach.
Refraction is also responsible for rainbows and for the splitting of white light into a rainbow-spectrum as it passes through a glass prism. Glass has a higher refractive index than air and the different frequencies of light travel at different speeds (dispersion), causing them to be refracted at different angles, so that you can see them. The different frequencies correspond to different colors observed.
While refraction allows for beautiful phenomena such as rainbows it may also produce peculiar optical phenomena, such as mirages and Fata Morgana. These are caused by the change of the refractive index of air with temperature.
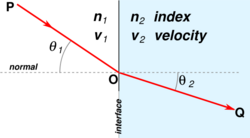
Snell's law is used to calculate the degree to which light is refracted when traveling from one medium to another.
Recently some metamaterials have been created which have a negative refractive index. With metamaterials, we can also obtain the total refraction phenomena when the wave impedances of the two media are matched. There is no reflected wave.
Also, since refraction can make objects appear closer than they are, it is responsible for allowing water to magnify objects. First, as light is entering a drop of water, it slows down. If the water's surface is not flat, then the light will be bent into a new path. This round shape will bend the light outwards and as it spreads out, the image you see gets larger.
Refractive index
The refractive index (or index of refraction) of a medium is the inverse ratio of the phase velocity (defined below) of a wave phenomenon such as light or sound, and the phase velocity in a reference medium (substance that the wave passes through). It is most commonly used in the context of light with vacuum as a reference medium, although historically other reference media (e.g. air at a standard pressure and temperature) have been common. It is usually given the symbol n, In the case of light, it equals
- ,
where εr is the material's relative permittivity (how a material affects an electric field), and μr is its relative permeability (how a material reacts to a magnetic field). For most materials, μr is very close to 1 at optical frequencies, therefore n is approximately . n may be less than 1 and this has practical technical applications, such as effective mirrors for X-rays based on total internal reflection.
The phase velocity is defined as the rate at which any part of the waveform travels through space; that is, the rate at which the phase of the waveform is moving. The group velocity is the rate that the envelope of the waveform is propagating; that is, the rate of variation of the amplitude (the maximum up and down motion) of the waveform. It is the group velocity, the velocity at which the crests and troughs of a wave move through space, that (almost always) represents the rate that information (and energy) may be transmitted by the wave—for example, the velocity at which a pulse of light travels down an optical fiber.
The speed of light
The speed of all electromagnetic radiation in vacuum is the same, approximately 3×108 meters per second, and is denoted by c. Therefore, if v is the phase velocity of radiation of a specific frequency in a specific material, the refractive index is given by
- .
This number is typically greater than one: the higher the index of the material, the more the light is slowed down. However, at certain frequencies (e.g., X-rays), n will actually be smaller than one. This does not contradict the theory of relativity, which holds that no information-carrying signal can ever propagate faster than c, because the phase velocity is not the same as the group velocity or the signal velocity, same as group velocity except when the wave is passing through an absorptive medium.
Sometimes, a "group velocity refractive index," usually called the group index is defined:
where vg is the group velocity. This value should not be confused with n, which is always defined with respect to the phase velocity.
At the microscale, an electromagnetic wave's phase velocity is slowed in a material because the electric field creates a disturbance in the charges of each atom (primarily the electrons) proportional (a relationship) to the permittivity. The charges will, in general, oscillate slightly out of phase with respect to the driving electric field. The charges thus radiate their own electromagnetic wave that is at the same frequency but with a phase delay. The macroscopic sum of all such contributions in the material is a wave with the same frequency but shorter wavelength than the original, leading to a slowing of the wave's phase velocity. Most of the radiation from oscillating material charges will modify the incoming wave, changing its velocity. However, some net energy will be radiated in other directions (see scattering).
If the refractive indices of two materials are known for a given frequency, then one can compute the angle by which radiation of that frequency will be refracted as it moves from the first into the second material from Snell's law.
Negative Refractive Index
Recent research has also demonstrated the existence of negative refractive index, which can occur if ε and μ are simultaneously negative. Not thought to occur naturally, it can be achieved with so called metamaterials. It offers the possibility of perfect lenses and other exotic phenomena such as a reversal of Snell's law.
List of indices of refraction
| Material | n at f=5.09x1014 Hz |
|---|---|
| Vacuum | 1 (exactly) |
| Helium | 1.000036 |
| Air @ STP | 1.0002926 |
| Carbon dioxide | 1.00045 |
| Water Ice | 1.31 |
| Liquid Water (20°C) | 1.333 |
| Cryolite | 1.338 |
| Acetone | 1.36 |
| Ethanol | 1.36 |
| Teflon | 1.35 - 1.38 |
| Glycerol | 1.4729 |
| Acrylic glass | 1.490 - 1.492 |
| Rock salt | 1.516 |
| Crown glass (pure) | 1.50 - 1.54 |
| Salt (NaCl) | 1.544 |
| Polycarbonate | 1.584 - 1.586 |
| Flint glass (pure) | 1.60 - 1.62 |
| Crown glass (impure) | 1.485 - 1.755 |
| Bromine | 1.661 |
| Flint glass (impure) | 1.523 - 1.925 |
| Cubic zirconia | 2.15 - 2.18 |
| Diamond | 2.419 |
| Moissanite | 2.65 - 2.69 |
| Cinnabar (Mercury sulfide) | 3.02 |
| Gallium(III) phosphide | 3.5 |
| Gallium(III) arsenide | 3.927 |
| Silicon | 4.01 |
Many materials have well-characterized refractive indices, but these indices depend strongly on the frequency of light. Therefore, any numeric value for the index is meaningless unless the associated frequency is specified.
There are also weaker dependencies on temperature, pressure/stress, and so forth, as well as on precise material compositions. For many materials and typical conditions, however, these variations are at the percent level or less. It is therefore especially important to cite the source for an index measurement, if precision is required.
In general, an index of refraction is a complex number with both a real and an imaginary part, where the latter indicates the strength of absorption loss at a particular wavelength—thus, the imaginary part is sometimes called the extinction coefficient k. Such losses become particularly significant—for example, in metals at short wavelengths (such as visible light)—and must be included in any description of the refractive index.
Dispersion and absorption
In real materials, the polarization does not respond instantaneously to an applied field. This causes dielectric loss, which can be expressed by a permittivity that is both complex and frequency dependent. Real materials are not perfect insulators either, meaning they have non-zero Direct Current (DC) conductivity. Taking both aspects into consideration, we can define a complex index of refraction:
Here, n is the refractive index indicating the phase velocity, while κ is called the extinction coefficient, which indicates the amount of absorption loss when the electromagnetic wave propagates through the material. Both n and κ are dependent on the frequency.
The effect that n varies with frequency (except in vacuum, where all frequencies travel at the same speed c) is known as dispersion, and it is what causes a prism to divide white light into its constituent spectral colors, which is how rainbows are formed in rain or mists. Dispersion is also the cause of chromatic aberration in lenses.
Since the refractive index of a material varies with the frequency (and thus wavelength) of light, it is usual to specify the corresponding vacuum wavelength at which the refractive index is measured. Typically, this is done at various well-defined spectral emission lines; for example, nD is the refractive index at the Fraunhofer "D" line, the centre of the yellow sodium double emission at 589.29 nm wavelength.
The Sellmeier equation is an empirical formula that works well in describing dispersion, and Sellmeier coefficients are often quoted instead of the refractive index in tables. For some representative refractive indices at different wavelengths, see list of indices of refraction.
As shown above, dielectric loss and non-zero DC conductivity in materials cause absorption. Good dielectric materials such as glass have extremely low DC conductivity, and at low frequencies the dielectric loss is also negligible, resulting in almost no absorption (κ ≈ 0). However, at higher frequencies (such as visible light), dielectric loss may increase absorption significantly, reducing the material's transparency to these frequencies.
The real and imaginary parts of the complex refractive index are related through use of the Kramers-Kronig relations. For example, one can determine a material's full complex refractive index as a function of wavelength from an absorption spectrum of the material.
Birefringence

The refractive index of certain media may be different depending on the polarization and direction of propagation of the light through the medium. This is known as birefringence and is described by the field of crystal optics.
Nonlinearity
The strong electric field of high intensity light (such as output of a laser) may cause a medium's refractive index to vary as the light passes through it, giving rise to nonlinear optics. If the index varies quadratically with the field (linearly with the intensity), it is called the optical Kerr effect and causes phenomena such as self-focusing and self phase modulation. If the index varies linearly with the field (which is only possible in materials that do not possess inversion symmetry), it is known as the Pockels effect.
Inhomogeneity
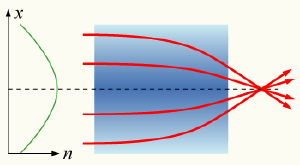
If the refractive index of a medium is not constant, but varies gradually with position, the material is known as a gradient-index medium and is described by gradient index optics. Light traveling through such a medium can be bent or focussed, and this effect can be exploited to produce lenses, some optical fibers and other devices. Some common mirages are caused by a spatially varying refractive index of air.
Applications
The refractive index of a material is the most important property of any optical system that uses the property of refraction. It is used to calculate the focusing power of lenses and the dispersive power of prisms.
Since refractive index is a fundamental physical property of a substance, it is often used to identify a particular substance, confirm its purity, or measure its concentration. Refractive index is used to measure solids (glasses and gemstones), liquids, and gases. Most commonly, it is used to measure the concentration of a solute in an aqueous solution. A refractometer is the instrument used to measure refractive index. For a solution of sugar, the refractive index can be used to determine the sugar content.
In medicine, particularly ophthalmology and optometry, the technique of refractometry utilizes the property of refraction for administering eye tests. This is a clinical test in which a phoropter is used to determine the eye's refractive error and, based on that, the best corrective lenses to be prescribed. A series of test lenses in graded optical powers or focal lengths are presented, to determine which ones provide the sharpest, clearest vision.
Alternative meaning: Refraction in metallurgy
In metallurgy, the term refraction has another meaning. It is a property of metals that indicates their ability to withstand heat. Metals with a high degree of refraction are referred to as refractory. These metals have high melting points, derived from the strong interatomic forces that are involved in metal bonds. Large quantities of energy are required to overcome these forces.
Examples of refractory metals include molybdenum, niobium, tungsten, and tantalum. Hafnium carbide is the most refractory binary compound known, with a melting point of 3,890 degrees C.[1][2]
See also
ReferencesISBN links support NWE through referral fees
- Fishbane, Paul M., et al. 2005. Physics for Scientists and Engineers, 3rd ed. Upper Saddle River, NJ: Pearson Education. ISBN 0131418815.
- Hecht, Jeff. 2006. Red Light Debut for Exotic 'Metamaterial.' NewScientist.com News Service. 13:38. Retrieved March 28, 2007.
- Henderson, Tom. 2004. Refraction and the Ray Model of Light. The Physics Classroom. Retrieved February 20, 2007.
- Ward, David W., Keith A. Nelson, and Kevin J. Webb. 2005. On the Physical Origins of the Negative Index of Refraction. New Journal of Physics 7:213. Retrieved March 28, 2007.
External links
All links retrieved December 7, 2022.
- Refraction through a Prism. (Java simulation.)
- Index of Refraction - Eric Weisstein's World of Physics.
- Index of Refraction - Hyperphysics. (List of refractive indices.)
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
- Refraction history
- Refractive_index history
- List_of_indices_of_refraction history
- Refraction_(metallurgy) history
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.