Focal length

The focal point F and focal length f of a positive (convex) lens, a negative (concave) lens, a concave mirror, and a convex mirror.

The focal length of an optical system is a property that provides a measure of how strongly the system converges (focuses) or diverges (diffuses) light. The optical system may consist of a lens or mirror or some combination of lenses and mirrors. A system with a shorter focal length has greater optical power than one with a long focal length.

Knowledge of this property is useful for the construction of various optical devices, such as eyeglasses, cameras, telescopes, and microscopes.

Thin lens approximation

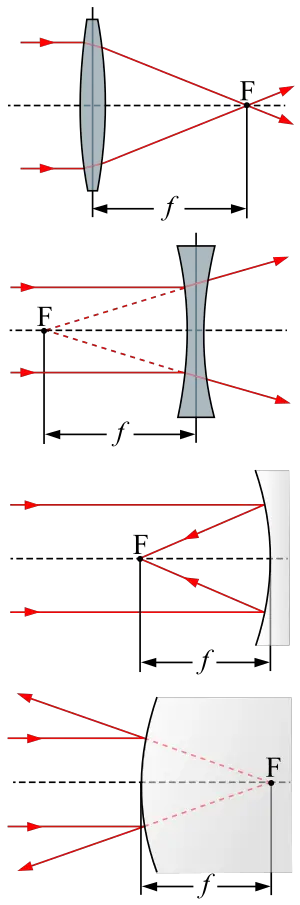
For a thin lens in air, the focal length is the distance from the center of the lens to the principal foci (or focal points) of the lens. For a converging lens (for example a convex lens), the focal length is positive, and is the distance at which a beam of collimated light will be focused to a single spot. For a diverging lens (for example a concave lens), the focal length is negative, and is the distance to the point from which a collimated beam appears to be diverging after passing through the lens.

General optical systems

For a thick lens (one which has a non-negligible thickness), or an imaging system consisting of several lenses and/or mirrors (e.g., a photographic lens or a telescope), the focal length is often called the effective focal length (EFL), to distinguish it from other commonly-used parameters:

Front focal length (FFL) or Front focal distance (FFD) is the distance from the front focal point of the system to the vertex of the first optical surface.^[1]
Back focal length (BFL) or Back focal distance (BFD) is the distance from the vertex of the last optical surface of the system to the rear focal point.^[1]

For an optical system in air, the effective focal length gives the distance from the front and rear principal planes to the corresponding focal points. If the surrounding medium is not air, then the distance is multiplied by the refractive index of the medium. Some authors call this distance the front (rear) focal length, distinguishing it from the front (rear) focal distance,\, defined above.^[1]

In general, the focal length or EFL is the value that describes the ability of the optical system to focus light, and is the value used to calculate the magnification of the system. The other parameters are used in determining where an image will be formed for a given object position.

For the case of a lens of thickness d in air, and surfaces with radii of curvature R₁ and R₂, the effective focal length f is given by:

{\frac {1}{f}}=(n-1)\left[{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right],

where n is the refractive index of the lens medium. The quantity 1/f is also known as the optical power of the lens.

The corresponding front focal distance is:

{\mbox{FFD}}=f\left(1+{\frac {(n-1)d}{nR_{2}}}\right),

and the back focal distance:

{\mbox{BFD}}=f\left(1-{\frac {(n-1)d}{nR_{1}}}\right).

In the sign convention used here, the value of R₁ will be positive if the first lens surface is convex, and negative if it is concave. The value of R₂ is positive if the second surface is concave, and negative if convex. Note that sign conventions vary between different authors, which results in different forms of these equations depending on the convention used.

For a spherically curved mirror in air, the magnitude of the focal length is equal to the radius of curvature of the mirror divided by two. The focal length is positive for a concave mirror, and negative for a convex mirror. In the sign convention used in optical design, a concave mirror has negative radius of curvature, so

f=-{R \over 2}

,

where $R$ is the radius of curvature of the mirror's surface.^[2]

In photography

How focal length affects photograph composition: adjusting the camera's distance from the main subject while changing focal length, the main subject can remain the same size, while the other at a different distance changes size. The dolly zoom is based on this effect.

When a photographic lens is set to "infinity," its rear nodal point is separated from the sensor or film, at the focal plane, by the lens's focal length. Objects far away from the camera then produce sharp images on the sensor or film, which is also at the image plane. Photographers sometimes refer to the image plane as the focal plane; these planes coincide when the object is at infinity, but for closer objects the focal plane is fixed, relative to the lens, and the image plane moves, by the standard optical definitions.

The focal length of a lens determines the magnification at which it images distant objects. The focal length of a lens is equal to the distance between the image plane and a pinhole (see pinhole camera model) that images distant small objects the same size as the lens in question. Combining this definition with an assumption of rectilinear imaging (that is, with no image distortion) leads to a simple geometric model the photographers use for computing the angle of view of a camera.

To render closer objects in sharp focus, the lens must be adjusted to increase the distance between the rear nodal point and the film, to put the film at the image plane. The focal length $f$ , the distance from the front nodal point to the object to photograph $S_{1}$ , and the distance from the rear nodal point to the image plane $S_{2}$ are then related by:

{\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{f}}

.

As $S_{1}$ is decreased, $S_{2}$ must be increased. For example, consider a normal lens for a 35 mm camera with a focal length of $f=50{\text{ mm}}$ . To focus a distant object ( $S_{1}\approx \infty$ ), the rear nodal point of the lens must be located a distance $S_{2}=50{\text{ mm}}$ from the image plane. To focus an object 1 m away ( $S_{1}=1000{\text{ mm}}$ ), the lens must be moved 2.6 mm further away from the image plane, to $S_{2}=52.6{\text{ mm}}$ .

Note that some simple and usually inexpensive cameras have fixed focus lenses which cannot be adjusted.

Focal lengths are usually specified in millimeters (mm), but older lenses marked in centimeters (cm) and inches are still to be found. The angle of view depends on the ratio between the focal length and the film size.

A lens with a focal length about equal to the diagonal size of the film or sensor format is known as a normal lens; its angle of view is similar to the angle subtended by a large-enough print viewed at a typical viewing distance of the print diagonal, which therefore yields a normal perspective when viewing the print;^[3] this angle of view is about 53 degrees diagonally. For full-frame, 35mm-format cameras, the diagonal is 43 mm and a typical "normal" lens has a 50 mm focal length. A lens with a focal length shorter than normal is often referred to as a wide-angle lens (typically 35 mm and less, for 35mm-format cameras), while a lens significantly longer than normal may be referred to as a telephoto lens (typically 85 mm and more, for 35mm-format cameras), though the use of the term is inaccurate as it implies specific optical design qualities that may or may not apply to a given lens.

Due to the popularity of the 35 mm standard, camera–lens combinations are often described in terms of their 35 mm equivalent focal length, that is, the focal length of a lens that would have the same angle of view, or field of view, if used on a full-frame 35 mm camera. Use of a 35 mm equivalent focal length is particularly common with digital cameras, which often use sensors smaller than 35 mm film, and so require correspondingly shorter focal lengths to achieve a given angle of view, by a factor known as the crop factor.

Notes

↑ ^1.0 ^1.1 ^1.2 John E. Greivenkamp, SPIE Field Guides, v. FG01 (Bellingham, WA: SPIE Press, 2004, ISBN 0819452947).
↑ The equation given here depends on an arbitrary sign convention, as explained on the page. Some books use a different sign convention.
↑ Leslie D. Stroebel, View Camera Technique, 7th ed. (Boston: Focal Press, 1999, ISBN 0240803450).

References
ISBN links support NWE through referral fees

Greivenkamp, John E. Field Guide to Geometrical Optics. SPIE Field Guides, v. FG01. Bellingham, WA: SPIE Press, 2004. ISBN 0819452947
Hecht, Eugene. Optics, 4th ed. Reading, MA: Addison-Wesley, 2002. ISBN 0805385665
Stroebel, Leslie D. View Camera Technique, 7th ed. Boston: Focal Press, 1999. ISBN 0240803450

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

Focal length ^history

The history of this article since it was imported to New World Encyclopedia:

History of "Focal length"

Note: Some restrictions may apply to use of individual images which are separately licensed.

[Greivenkamp-1] 1.0 ^1.1 ^1.2 John E. Greivenkamp, SPIE Field Guides, v. FG01 (Bellingham, WA: SPIE Press, 2004, ISBN 0819452947).

[2] The equation given here depends on an arbitrary sign convention, as explained on the page. Some books use a different sign convention.

[3] Leslie D. Stroebel, View Camera Technique, 7th ed. (Boston: Focal Press, 1999, ISBN 0240803450).

[1]

[2]

[3]