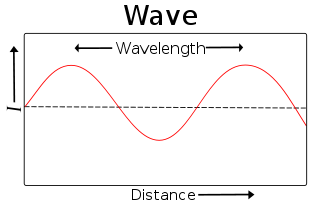
Wavelength

Wavelength of a sine wave.

In physics, wavelength is the distance between repeating units of a propagating wave at a given frequency. It is commonly designated by the Greek letter lambda (λ). Examples of wavelike phenomena are light, water waves, and sound waves.

The properties of a wave vary with the type of wave. For example, in a sound wave, the air pressure oscillates, but in the case of light and other forms of electromagnetic radiation, there is variation in the strength of the electric and magnetic fields.

The wavelength (and frequency) of visible light varies with color of the light. For example, the wavelength of deep red is roughly 700 nanometers (nm), that of violet is roughly 400 nm. The wavelengths of sound frequencies audible to the human ear (20 Hz–20 kHz) are between approximately 17 meters (m) and 17 millimeters (mm). Thus the wavelengths of audible sound waves are much longer than those of visible light.

Relationship with frequency

The wavelength of a wave (or wavelike phenomenon) is related to the frequency by the formula: wavelength = wave speed / frequency. Thus, the wavelength of a wave is inversely proportional to the frequency of the wave. Waves with higher frequencies have shorter wavelengths; those with lower frequencies have longer wavelengths, assuming the speed of the wave is the same.

In symbols, the equation for wavelength may be written as:

$\lambda ={\frac {v}{f}}$

where λ represents the wavelength, v is the propagation speed of the wave, and f is its frequency.

In the case of electromagnetic radiation, such as light, in a vacuum, the velocity of the wave is the speed of light, 299,792,458 meters per second (m/s) or about 3×10⁸ m/s. For sound waves in air, this is the speed of sound, 345 m/s (1238 km/h) in air at room temperature and atmospheric pressure. Usually, SI units are used, where the wavelength is expressed in meters, the frequency in Hertz (Hz), and the propagation velocity in m/s.

For example, the wavelength for a 100 MHz electromagnetic (radio) wave is about: λ = 3×10⁸ m/s divided by 100×10⁶ Hz = 3 meters. Electronic engineers often use a shortcut formula: wavelength λ in meters = 300 Megameters (Mm)/s divided by the frequency in MHz, to avoid counting the (many) zero digits in the decimal or scientific notations.

It should be noted that for many wave phenomena, wavelength is not the distance that particles travel during a period. For instance, in acoustics and water waves, the particle displacements during a period are only a small fraction of the wavelength, apart from extreme conditions like breaking waves and shock waves.

It should also be noted that frequency and wavelength can change independently, but only when the speed of the wave changes. For example, when light enters another medium, its speed and wavelength change while its frequency does not.

In non-vacuum media

The speed of light in most media is lower than in vacuum, which means that the same frequency will correspond to a shorter wavelength in the medium than in vacuum. The wavelength in the medium is

$\lambda '={\frac {\lambda _{0}}{n}}$

where n is the refractive index of the medium. Wavelengths of electromagnetic radiation are usually quoted in terms of the vacuum wavelength, unless specifically indicated as the "wavelength in the medium." In acoustics, where a medium is essential for the waves to exist, the term wavelength is always the wavelength in the medium. Then the refractive index depends on the mean properties of the medium, for instance the mean pressure or changes in the material composition.

De Broglie wavelength of particles

Louis de Broglie postulated that all particles with momentum have a wavelength

$\lambda ={\frac {h}{p}}$

where h is Planck's constant, and p is the momentum of the particle. This hypothesis was at the basis of quantum mechanics. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electrons in a CRT display have a De Broglie wavelength of about 10^-13 m.

See also

• Amplitude
• Electromagnetic spectrum
• Frequency
• Light
• Sound
• Wave

References

ISBN links support NWE through referral fees

• French, A.P. 1971. Vibrations and Waves. The M.I.T. Introductory Physics Series. New York: Norton. ISBN 0393099245
• Pain, H.J. 2005. The Physics of Vibrations and Waves. Chichester: John Wiley. ISBN 978-0470012963
• Reitz, John R., Frederick J. Milford, and Robert W. Christy. 1992. Foundations of Electromagnetic Theory. Reading, MA: Addison-Wesley Pub. Co. ISBN 0201526247
• Serway, Raymond A., and John W. Jewett. 2004. Physics for Scientists and Engineers, 6th ed. Belmont, CA: Brooks/Cole. ISBN 0534408427
• Tipler, Paul Allen, and Gene Mosca. 2004. Physics for Scientists and Engineers, 5th ed. New York: W.H. Freeman. ISBN 0716743892
• Wilson, Jerry D., and Anthony J. Buffa. 2003. College Physics. Upper Saddle River, NJ: Prentice Hall. ISBN 0130676446

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Wavelength  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Wavelength"

Note: Some restrictions may apply to use of individual images which are separately licensed.