Orbit
In physics, an orbit is the path that an object makes around another object while under the influence of a source of centripetal force. Most common use of orbit indicates that of a celestial body revolving around a star or planet under the influence of gravity. When more than one body is orbiting a central body, interaction among the orbiting bodies also exists, which may cause changes of their orbits. While planets in the Solar System form a stable state over the major part of the history of the Solar System, smaller objects such as asteroids and comets keep changing their orbits and eventually will be cast out of the Solar System or will collide with other bodies. Orbits in celestial bodies inspired scientists to derive electron orbitals bound to an atom, and others to believe it as a manifestation of God's eternal principles of creation.
History
Orbits were first analyzed mathematically by Johannes Kepler who formulated his results in his three laws of planetary motion based on Tycho Brahe's observational data. First, he found that the orbits of the planets in our solar system are elliptical, not circular (or epicyclic), as had previously been believed based on Ptolemy's view, and that the sun is not located at the center of the orbits, but rather at one focus. Second, he found that the orbital speed of each planet is not constant, as had previously been thought, but rather that the speed of the planet depends on the planet's distance from the sun. And third, Kepler found a universal relationship between the orbital properties of all the planets orbiting the sun. For each planet, the cube of the planet's distance from the sun, measured in astronomical units (AU), is equal to the square of the planet's orbital period, measured in Earth years. Jupiter, for example, is approximately 5.2 AU from the sun and its orbital period is 11.86 Earth years. So 5.2 cubed equals 11.86 squared, as predicted.
Isaac Newton demonstrated that Kepler's laws were derivable from his theory of gravitation and that, in general, the orbits of bodies responding to the force of gravity were conic sections. Newton showed that a pair of bodies follow orbits of dimensions that are in inverse proportion to their masses about their common center of mass. Where one body is much more massive than the other, it is a convenient approximation to take the center of mass as coinciding with the center of the more massive body.
Planetary orbits
Within a planetary system, planets, dwarf planets, asteroids (a.k.a. minor planets), comets, interplanetary dusts, and space debris orbit the central star in elliptical orbits. A comet in a parabolic or hyperbolic orbit about a central star is not gravitationally bound to the star and therefore is not considered part of the star's planetary system. To date, no comet has been observed in our solar system with a distinctly hyperbolic orbit. Bodies which are gravitationally bound to one of the planets in a planetary system, either natural or artificial satellites, follow orbits about that planet.
Owing to mutual gravitational perturbations, the eccentricities of the orbits of the planets in our solar system vary over time. Mercury, the smallest planet in the Solar System, has the most eccentric orbit. At the present epoch, Mars has the next largest eccentricity while the smallest eccentricities are those of the orbits of Venus and Neptune.
As two objects orbit each other, the periapsis is that point at which the two objects are closest to each other and the apoapsis is that point at which they are the farthest from each other.
In the elliptical orbit, the center of mass of the orbiting-orbited system will sit at one focus of both orbits, with nothing present at the other focus. As a planet approaches periapsis, the planet will increase in velocity. As a planet approaches apoapsis, the planet will decrease in velocity.
Understanding orbits
There are a few common ways of understanding orbits.
- As the object moves sideways, it falls toward the orbited object. However it moves so quickly that the curvature of the orbited object will fall away beneath it.
- A force, such as gravity, pulls the object into a curved path as it attempts to fly off in a straight line.
- As the object falls, it moves sideways fast enough (has enough tangential velocity) to miss the orbited object. This understanding is particularly useful for mathematical analysis, because the object's motion can be described as the sum of the three one-dimensional coordinates oscillating around a gravitational center.
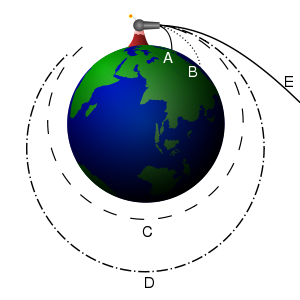
As an illustration of an orbit around a planet, the much-used cannon model may prove useful (see image below). Imagine a cannon sitting on top of a tall mountain, which fires a cannonball horizontally. The mountain needs to be very tall, so that the cannon will be above the Earth's atmosphere and we can ignore the effects of air friction on the cannon ball.
If the cannon fires its ball with a low initial velocity, the trajectory of the ball curves downwards and hits the ground (A). As the firing velocity is increased, the cannonball hits the ground farther (B) away from the cannon, because while the ball is still falling towards the ground, the ground is increasingly curving away from it (see first point, above). All these motions are actually "orbits" in a technical sense‚ÄĒthey are describing a portion of an elliptical path around the center of gravity‚ÄĒbut the orbits are of course interrupted by striking the earth.
If the cannonball is fired with sufficient velocity, the ground curves away from the ball at least as much as the ball falls‚ÄĒso the ball never strikes the ground. It is now in what could be called a non-interrupted, or circumnavigating, orbit. For any specific combination of height above the center of gravity, and mass of the object being fired, there is one specific firing velocity that produces a circular orbit, as shown in (C).
As the firing velocity is increased beyond this, a range of elliptical orbits are produced; one is shown in (D). If the initial firing is above the surface of the earth as shown, there will also be elliptical orbits at slower velocities; these will come closest to the earth opposite the firing the point.
At a faster velocity called escape velocity, again depending on the firing height and mass of the object, an infinite orbit such as (E) is produced‚ÄĒfirst a range of parabolic orbits, and at even faster velocities a range of hyperbolic orbits. In a practical sense, both of these infinite orbit types mean the object is "breaking free" of the planet's gravity, and "going off into space."
The velocity relationship of two objects with mass can thus be considered in four practical classes, with subtypes:
1. No orbit
2. Interrupted orbits
- Range of interrupted elliptical paths
3. Circumnavigating orbits
- Range of elliptical paths with closest point opposite firing point
- Circular path
- Range of elliptical paths with closest point at firing point
4. Infinite orbits
- Parabolic paths
- Hyperbolic paths
Newton's laws of motion
For a system of only two bodies that are influenced only by their mutual gravity, their orbits can be exactly calculated by Newton's laws of motion and gravity, assuming the effect of general relativity is insignificant. Briefly, the sum of the forces will equal the mass times its acceleration. Gravity is proportional to mass (gravitational mass is equal to inertial mass), and falls off proportionally to the square of distance.
To calculate, it is convenient to describe the motion in a coordinate system that is centered on the heavier body, and we can say that the lighter body is in orbit around the heavier body.
An unmoving body that's far from a large object has more gravitational potential energy than one that's close, because it can fall farther.
With two bodies, an orbit is a conic section. The orbit can be open (so the object never returns) or closed (returning), depending on the total kinetic + potential energy of the system. In the case of an open orbit, the speed at any position of the orbit is at least the escape velocity for that position, in the case of a closed orbit, always less.
An open orbit has the shape of a hyperbola (when the velocity is greater than the escape velocity), or a parabola (when the velocity is exactly the escape velocity). The bodies approach each other for awhile, curve around each other around the time of their closest approach, and then separate again forever. This may be the case with some comets if they come from outside the solar system.
A closed orbit has the shape of an ellipse. In the special case that the orbiting body is always the same distance from the center, it is also the shape of a circle. Otherwise, the point where the orbiting body is closest to Earth is the perigee, called periapsis (less properly, "perifocus" or "pericentron") when the orbit is around a body other than Earth. The point where the satellite is farthest from Earth is called apogee, apoapsis, or sometimes apifocus or apocentron. A line drawn from periapsis to apoapsis is the line-of-apsides. This is the major axis of the ellipse, the line through its longest part.
Orbiting bodies in closed orbits repeat their path after a constant period of time. This motion is described by the empirical laws of Kepler, which can be mathematically derived from Newton's laws. These can be formulated as follows:
- The orbit of a planet around the Sun is an ellipse, with the Sun in one of the focal points of the ellipse. Therefore the orbit lies in a plane, called the orbital plane. The point on the orbit closest to the attracting body is the periapsis. The point farthest from the attracting body is called the apoapsis. There are also specific terms for orbits around particular bodies; things orbiting the Sun have a perihelion and aphelion, things orbiting the Earth have a perigee and apogee, and things orbiting the Moon have a perilune and apolune (or, synonymously, periselene and aposelene). An orbit around any star, not just the Sun, has a periastron and an apastron.
- As the planet moves around its orbit during a fixed amount of time, the line from Sun to planet sweeps a constant area of the orbital plane, regardless of which part of its orbit the planet traces during that period of time. This means that the planet moves faster near its perihelion than near its aphelion, because at the smaller distance it needs to trace a greater arc to cover the same area. This law is usually stated as "equal areas in equal time."
- For each planet, the ratio of the third power of its semi-major axis to the second power of its period is the same constant value for all planets.
Except for special cases like Lagrangian points, no method is known to solve the equations of motion for a system with four or more bodies. The two-body solutions were published by Newton in Principia in 1687. In 1912, Karl Fritiof Sundman developed a converging infinite series that solves the 3-body problem, however it converges too slowly to be of much use.
Instead, orbits can be approximated with arbitrarily high accuracy. These approximations take two forms.
One form takes the pure elliptic motion as a basis, and adds perturbation terms to account for the gravitational influence of multiple bodies. This is convenient for calculating the positions of astronomical bodies. The equations of motion of the moon, planets and other bodies are known with great accuracy, and are used to generate tables for celestial navigation. Still there are secular phenomena that have to be dealt with by post-newtonian methods.
The differential equation form is used for scientific or mission-planning purposes. According to Newton's laws, the sum of all the forces will equal the mass times its acceleration (F = ma). Therefore accelerations can be expressed in terms of positions. The perturbation terms are much easier to describe in this form. Predicting subsequent positions and velocities from initial ones corresponds to solving an initial value problem. Numerical methods calculate the positions and velocities of the objects a tiny time in the future, then repeat this. However, tiny arithmetic errors from the limited accuracy of a computer's math accumulate, limiting the accuracy of this approach.
Differential simulations with large numbers of objects perform the calculations in a hierarchical pairwise fashion between centers of mass. Using this scheme, galaxies, star clusters and other large objects have been simulated.
Orbital period
The orbital period is the time it takes a planet (or another object) to make one full orbit. There are several kinds of orbital periods for objects around the Sun, as given below.
- The sidereal period is the time that it takes the object to make one full orbit around the Sun, relative to the stars. This is considered to be an object's true orbital period.
- The synodic period is the time that it takes for the object to reappear at the same point in the sky, relative to the Sun, as observed from Earth‚ÄĒthat is, returns to the same elongation. This is the time that elapses between two successive conjunctions with the Sun and is the object's Earth-apparent orbital period. The synodic period differs from the sidereal period since Earth itself revolves around the Sun.
- The draconitic period is the time that elapses between two passages of the object at its ascending node, the point of its orbit where it crosses the ecliptic from the southern to the northern hemisphere. It differs from the sidereal period because the object's line of nodes typically precesses or recesses slowly.
- The anomalistic period is the time that elapses between two passages of the object at its perihelion, the point of its closest approach to the Sun. It differs from the sidereal period because the object's semimajor axis typically precesses or recesses slowly.
- The tropical period is the time that elapses between two passages of the object at right ascension zero. It is slightly shorter than the sidereal period because the vernal point precesses.
Orbital decay
If some part of a body's orbit enters an atmosphere, its orbit can decay because of drag. At each periapsis, the object scrapes the air, losing energy. Each time, the orbit grows less eccentric (more circular) because the object loses kinetic energy precisely when that energy is at its maximum. This is similar to the effect of slowing a pendulum at its lowest point; the highest point of the pendulum's swing becomes lower. With each successive slowing more of the orbit's path is affected by the atmosphere and the effect becomes more pronounced. Eventually, the effect becomes so great that the maximum kinetic energy is not enough to return the orbit above the limits of the atmospheric drag effect. When this happens the body will rapidly spiral down and intersect the central body.
The bounds of an atmosphere vary wildly. During solar maxima, the Earth's atmosphere causes drag up to a hundred kilometres higher than during solar minimums. Some satellites with long conductive tethers can also decay because of electromagnetic drag from the Earth's magnetic field. Basically, the wire cuts the magnetic field, and acts as a generator. The wire moves electrons from the near vacuum on one end to the near-vacuum on the other end. The orbital energy is converted to heat in the wire.
Orbits can be artificially influenced through the use of rocket motors which change the kinetic energy of the body at some point in its path. This is the conversion of chemical or electrical energy to kinetic energy. In this way, changes in the orbit shape or orientation can be facilitated. Another method of artificially influencing an orbit is through the use of solar sails or magnetic sails.
Orbital decay can also occur due to tidal forces for objects below the synchronous orbit for the body they are orbiting. The gravity of the orbiting object raises tidal bulges in the primary, and since below the synchronous orbit the orbiting object is moving faster than the body's surface the bulges lag a short angle behind it. The gravity of the bulges is slightly off of the primary-satellite axis and thus has a component along the satellite's motion. The near bulge slows the object more than the far bulge speeds it up, and as a result the orbit decays. Conversely, the gravity of the satellite on the bulges applies torque on the primary and speeds up its rotation. Artificial satellites are too small to have an appreciable tidal effect on the planets they orbit, but several moons in the solar system are undergoing orbital decay by this mechanism. Mars' innermost moon Phobos is a prime example, and is expected to either impact Mars' surface or break up into a ring within 50 million years.
Finally, orbits can decay or develop via the emission of heat absorbed from sunlight shone on the body. Depending on more detailed mechanism and condition, this effect is called as either Poynting-Robertson effect which is effective on dusts or Yarkovsky effect which is effective on small asteroids.
Synchronous orbits
A synchronous orbit is an orbit in which an orbiting body (usually a satellite) has a period equal to the average rotational period of the body being orbited (usually a planet), and in the same direction of rotation as that body.
A satellite in a synchronous orbit that is both equatorial and circular will appear to be suspended motionless above a point on the orbited planet's equator. A synchronous orbit about the Earth that is circular and lies in the equatorial plane is called a geostationary orbit. If the orbit is inclined to the Earth's equator or is noncircular, it is called a geosynchronous orbit. The corresponding terms for synchronous orbits around the planet Mars are areostationary and areosynchronous orbits.
A body in a non-equatorial synchronous orbit will appear to oscillate north and south above a point on the planet's equator, while a body in an elliptical orbit (in the equatorial plane) will appear to oscillate east and west. The combination of these two motions produces a figure-eight pattern as seen from the orbited body, and it is called an "analemma."
Synchronous orbits are commonly employed by artificial satellites used for communication.
Geosynchronous orbit
A geosynchronous orbit is an orbit around the Earth with an orbital period matching the Earth's sidereal rotation period. This synchronization means that for an observer at a fixed location on Earth, a satellite in a geosynchronous orbit returns to exactly the same place in the sky at exactly the same time each day. The special case of a geosynchronous orbit that is circular and directly above the equator is called a geostationary orbit.
A semisynchronous orbit has an orbital period of 0.5 sidereal days, i.e. 11 h 58 min. Relative to the Earth's surface it has twice this period. An example is the Molniya orbit.
Orbital characteristics
Every geosynchronous orbit has a semi-major axis of 42,164 km (26,200 miles). When the orbit has a non-zero inclination or eccentricity, the ground track of a satellite in that orbit is a more or less distorted figure-eight, returning to the same places once per sidereal day.
Geostationary orbit
A geostationary orbit (GEO) is a circular geosynchronous orbit directly above the Earth's equator‚ÄĒthat is, at 0¬į inclination and zero orbital eccentricity. From the ground, a geostationary object appears motionless in the sky.
A satellite in this orbit appears stationary with respect to a fixed point on the rotating Earth. As a result, an antenna can point in a fixed direction and maintain a link with the satellite. It is therefore the orbit of most interest to operators of artificial satellites, including communication, television, and weather satellites.
Geostationary orbits can only be achieved very close to the ring 35,786 kilometers (km) (22,240 statute miles) above mean sea level. This altitude is significant because it produces an orbital period equal to the Earth's period of rotation, known as the sidereal day. In practice, this means that all geostationary satellites have to exist on this ring directly above the equator. Because the latitude is fixed at 0¬į, satellite locations may differ by longitude only.
A worldwide network of geostationary meteorological satellites is used to provide visible and infrared images of the Earth's surface and atmosphere. These satellite systems include:
- US GOES
- Meteosat, launched by the European Space Agency and operated by the European Weather Satellite Organization, EUMETSAT
- Japanese GMS
- India's INSAT series
Most commercial communications satellites and television satellites operate in geostationary orbits. (Russian television satellites have used elliptical Molniya and Tundra orbits due to the high latitudes of the receiving audience.) The first satellite placed into a geostationary orbit was Syncom-3, launched by a Delta-D rocket in 1964.
Practical limitations
A perfect stable geostationary orbit is an ideal that can only be approximated. In practice, the satellite will drift out of this orbit because of perturbations such as the solar wind, solarradiation pressure, variations in the Earth's gravitational field, and the gravitational effect of the Moon and Sun. For this reason, the satellite is equipped with thrusters that correct for these effects and maintain the orbit in a process known as stationkeeping. The consumption of thruster propellant for station keeping places a limitation on the lifetime of the satellite.
At the end of their service life, the satellites in geostationary orbit are decommissioned. They may continue to be used in inclined orbits (where the orbital track appears to follow a figure-of-eight loop centered on the Equator) or be raised to a "graveyard" disposal orbit.
Synchronous orbits around objects other than the Earth
Synchronous orbits exist around all moons, planets, stars and black holes ‚ÄĒ unless they rotate so slowly that the orbit would be outside their Hill sphere. Most inner moons of planets have synchronous rotation, so their synchronous orbits are, in practice, limited to their leading and trailing Lagrange points. Objects with chaotic rotations (such as Hyperion) are also problematic, as their synchronous orbits keep changing unpredictably.
Other geosynchronous orbits
Elliptical orbits can be and are designed for communications satellites that keep the satellite within view of its assigned ground stations or receivers. A satellite in an elliptical geosynchronous orbit will appear to oscillate in the sky from the viewpoint of a ground station, tracing an analemma in the sky. Satellites in highly elliptical orbits must be tracked by steerable ground stations.
Theoretically an active geosynchronous orbit can be maintained if forces other than gravity are also used to maintain the orbit, such as a solar sail. Such a statite can be geosynchronous in an orbit different (higher, lower, more or less elliptical, or some other path) from the conic section orbit formed by a gravitational body. Such devices are still theoretical.
A further form of geosynchronous orbit is obtained by the theoretical space elevator in which one end of the structure is tethered to the ground, maintaining a longer orbital period than by gravity alone if under tension.
Other definitions of geosynchronous orbit
- Geosynchronous orbit (GEO): a circular orbit, 35786 km above Earth's surface
The following orbits are special orbits that are also used to categorize orbits:
- Geostationary orbit (GSO): zero inclination geosynchronous orbit
- Supersynchronous orbit - a disposal / storage orbit above GSO/GEO. Satellites will drift in a westerly direction.
- Subsynchronous orbit - a drift orbit close to but below GSO/GEO. Used for satellites undergoing station changes in an eastern direction.
- Graveyard orbit - a supersynchronous orbit where spacecraft are intentionally placed at the end of their operational life.
History
The idea of a geosynchronous satellite for communication purposes was first published in 1928 by Herman Potońćnik. The geostationary orbit was first popularized by science fiction author Arthur C. Clarke in 1945 as a useful orbit for communications satellites. For this reason, this orbit is sometimes referred to as the Clarke orbit. Similarly, the Clarke Belt is the part of space approximately 35,786 km above mean sea level in the plane of the equator where near-geostationary orbits may be achieved.
The first communications satellite placed in a geosynchronous orbit was Syncom 2, launched in 1963. Geosynchronous orbits have been in common use ever since, including satellite television.
Initially, geostationary satellite also carried cellphone calls but are no longer used so predominantly for voice communication, partly due to the inherent disconcerting delay in getting information to the satellite and back (it takes light or radio about a quarter of a second to make the round trip, thus two parties talking via satellite will perceive about a half second delay in round-trip response). Similarly, international Internet connectivity has shifted away from satellite links.
Nearly all populated land locations on the Earth now have terrestrial communications facilities (microwave, fiber-optic), even undersea, with more than sufficient capacity. Satellite telephony is now mainly limited to small, isolated locations that have no terrestrial facilities, such as Canada's arctic islands, Antarctica, the far reaches of Alaska and Greenland, and ships at sea.
Role in development of the atomic theory
When atomic structure was first probed experimentally early in the twentieth century, an early picture of the atom portrayed it as a miniature solar system bound by the Coulomb force rather than by gravity. This was inconsistent with electrodynamics and the model was progressively refined as quantum theory evolved, but there is a legacy of the picture in the term orbital for the wave function of an energetically bound electron state.
See also
- Gravity
- Newton's laws of motion
- Kepler's laws of planetary motion
ReferencesISBN links support NWE through referral fees
- Abell, G. O., D. Morrison, and S.C. Wolff, 1991. Exploration of the Universe, 6th ed. Orlando, FL: Saunders College Publishing. ISBN 0030345847.
- Gingerich, O. 1993. The Eye of Heaven - Ptolemy, Copernicus, Kepler. New York: American Institute of Physics. ISBN 0883188635.
- Seeds, M.A. 1997. Foundations of Astronomy, 4th ed. Belmont, CA: Wadsworth Publishing Company. ISBN 0534260284.
External links
All links retrieved November 17, 2022.
- Orbit Terms Explained, Astronomy Terms for Kids.
- Orbital Mechanics (Rocket and Space Technology).
- Java simulation on orbital motion.
- List of Satellites in Geostationary Orbit
- Clarke Belt Snapshot Generator.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
- Orbit  history
- Orbital_period  history
- Synchronous_orbit  history
- Geosynchronous_orbit  history
- Geostationary_orbit  history
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.