Parabola

A parabola.

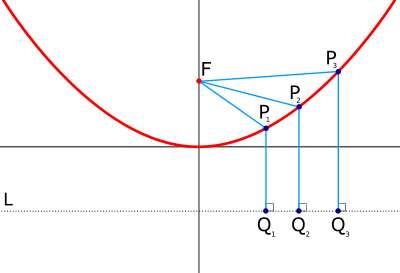
In mathematics, the parabola (from the Greek word παραβολή) is a conic section generated by the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface. A parabola can also be defined as locus of points in a plane which are equidistant from a given point (the focus) and a given line (the directrix).

A particular case arises when the plane is tangent to the conical surface. In this case, the intersection is a degenerate parabola consisting of a straight line.

The parabola is an important concept in abstract mathematics, but it is also seen with considerable frequency in the physical world, and there are many practical applications for the construct in engineering, physics, and other domains.

A parabola (shaded green) is a conic section.

A graph showing the reflective property, the directrix (green), and the lines connecting the focus and directrix to the parabola (blue).

Analytic geometry equations

In Cartesian coordinates, a parabola with an axis parallel to the y axis with vertex (h, k), focus (h, k + p), and directrix y = k - p, with p being the distance from the vertex to the focus, has the equation with axis parallel to the y-axis

$(x-h)^{2}=4p(y-k)\,$

or, alternatively with axis parallel to the x-axis

$(y-k)={\frac {1}{4p}}(x-h)^{2}\,$

More generally, a parabola is a curve in the Cartesian plane defined by an irreducible equation of the form

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,$

such that $B^{2}=4AC\,$, where all of the coefficients are real, where $A\not =0\,$ or $C\not =0\,$, and where more than one solution, defining a pair of points (x, y) on the parabola, exists. That the equation is irreducible means it does not factor as a product of two not necessarily distinct linear equations.

Other geometric definitions

Parabolas are conic sections.

A parabola may also be characterized as a conic section with an eccentricity of 1. As a consequence of this, all parabolas are similar. A parabola can also be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction. In this sense, a parabola may be considered an ellipse that has one focus at infinity. The parabola is an inverse transform of a cardioid.

A parabola has a single axis of reflective symmetry, which passes through its focus and is perpendicular to its directrix. The point of intersection of this axis and the parabola is called the vertex. A parabola spun about this axis in three dimensions traces out a shape known as a paraboloid of revolution.

The parabola is found in numerous situations in the physical world (see below).

Equations

(with vertex (h, k) and distance p between vertex and focus - note that if the vertex is below the focus, or equivalently above the directrix, p is positive, otherwise p is negative; similarly with horizontal axis of symmetry p is positive if vertex is to the left of the focus, or equivalently to the right of the directrix)

Cartesian

Vertical axis of symmetry

$(x-h)^{2}=4p(y-k)\,$

$y=a(x-h)^{2}+k\,$

$y=ax^{2}+bx+c\,$

${\mbox{where }}a={\frac {1}{4p}};\ \ b={\frac {-h}{2p}};\ \ c={\frac {h^{2}}{4p}}+k;\ \$

$h={\frac {-b}{2a}};\ \ k={\frac {4ac-b^{2}}{4a}}$.

$x(t)=2pt+h;\ \ y(t)=pt^{2}+k\,$

Horizontal axis of symmetry

$(y-k)^{2}=4p(x-h)\,$

$x=a(y-k)^{2}+h\,$

$x=ay^{2}+by+c\,$

${\mbox{where }}a={\frac {1}{4p}};\ \ b={\frac {-k}{2p}};\ \ c={\frac {k^{2}}{4p}}+h;\ \$

$h={\frac {4ac-b^{2}}{4a}};\ \ k={\frac {-b}{2a}}$.

$x(t)=pt^{2}+h;\ \ y(t)=2pt+k\,$

Semi-latus rectum and polar coordinates

In polar coordinates, a parabola with the focus at the origin and the directrix on the positive x-axis, is given by the equation

$r(1+\cos \theta )=l\,$

where l is the semilatus rectum: the distance from the focus to the parabola itself, measured along a line perpendicular to the axis. Note that this is twice the distance from the focus to the apex of the parabola or the perpendicular distance from the focus to the latus rectum.

Gauss-mapped form

A Gauss-mapped form: $(\tan ^{2}\phi ,2\tan \phi )$ has normal $(\cos \phi ,\sin \phi )$.

Derivation of the focus

Parabolic curve showing directrix (L) and focus (F). The distance from a given point P_n to the focus is always the same as the distance from P_n to a point Q_n directly below, on the directrix.

Given a parabola parallel to the y-axis with vertex (0,0) and with equation

$y=ax^{2},\qquad \qquad \qquad (1)$

then there is a point (0,f) — the focus — such that any point P on the parabola will be equidistant from both the focus and a line perpendicular to the axis of symmetry of the parabola (the linea directrix), in this case parallel to the x axis. Since the vertex is one of the possible points P, it follows that the linea directrix passes through the point (0,-f). So for any point P=(x,y), it will be equidistant from (0,f) and (x,-f). It is desired to find the value of f which has this property.

Let F denote the focus, and let Q denote the point at (x,-f). Line FP has the same length as line QP.

$\|FP\|={\sqrt {x^{2}+(y-f)^{2}}},$

$\|QP\|=y+f.$

$\|FP\|=\|QP\|$

${\sqrt {x^{2}+(ax^{2}-f)^{2}}}=ax^{2}+f\qquad$

Square both sides,

$x^{2}+(ax^{2}-f)^{2}=(ax^{2}+f)^{2}\qquad$

$=a^{2}x^{4}+f^{2}+2ax^{2}f\quad$

$x^{2}+a^{2}x^{4}+f^{2}-2ax^{2}f=a^{2}x^{4}+f^{2}+2ax^{2}f\quad$

Cancel out terms from both sides,

$x^{2}-2ax^{2}f=2ax^{2}f,\quad$

$x^{2}=4ax^{2}f.\quad$

Cancel out the x² from both sides (x is generally not zero),

$1=4af\quad$

$f={1 \over 4a}$

Now let p=f and the equation for the parabola becomes

$x^{2}=4py\quad$

Q.E.D.

All this was for a parabola centered at the origin. For any generalized parabola, with its equation given in the standard form

$y=ax^{2}+bx+c$,

the focus is located at the point

$\left({\frac {-b}{2a}},{\frac {-b^{2}}{4a}}+c+{\frac {1}{4a}}\right)$

and the directrix is designated by the equation

$y={\frac {-b^{2}}{4a}}+c-{\frac {1}{4a}}$

Reflective property of the tangent

The tangent of the parabola described by equation (1) has slope

${dy \over dx}=2ax={2y \over x}$

This line intersects the y-axis at the point (0,-y) = (0, - a x²), and the x-axis at the point (x/2,0). Let this point be called G. Point G is also the midpoint of points F and Q:

$F=(0,f),\quad$

$Q=(x,-f),\quad$

${F+Q \over 2}={(0,f)+(x,-f) \over 2}={(x,0) \over 2}=({x \over 2},0).$

Since G is the midpoint of line FQ, this means that

$\|FG\|\cong \|GQ\|,$

and it is already known that P is equidistant from both F and Q:

$\|PF\|\cong \|PQ\|,$

and, thirdly, line GP is equal to itself, therefore:

$\Delta FGP\cong \Delta QGP$

It follows that $\angle FPG\cong \angle GPQ$.

Line QP can be extended beyond P to some point T, and line GP can be extended beyond P to some point R. Then $\angle RPT$ and $\angle GPQ$ are vertical, so they are equal (congruent). But $\angle GPQ$ is equal to $\angle FPG$. Therefore $\angle RPT$ is equal to $\angle FPG$.

The line RG is tangent to the parabola at P, so any light beam bouncing off point P will behave as if line RG were a mirror and it were bouncing off that mirror.

Let a light beam travel down the vertical line TP and bounce off from P. The beam's angle of inclination from the mirror is $\angle RPT$, so when it bounces off, its angle of inclination must be equal to $\angle RPT$. But $\angle FPG$ has been shown to be equal to $\angle RPT$. Therefore the beam bounces off along the line FP: directly towards the focus.

Conclusion: Any light beam moving vertically downwards in the concavity of the parabola (parallel to the axis of symmetry) will bounce off the parabola moving directly towards the focus. (See parabolic reflector.)

What happens to a parabola when "b" varies?

Vertex of a parabola: Finding the y-coordinate

We know the x-coordinate at the vertex is $x=-{\frac {b}{2a}}$, so substitute it into the equation $ax^{2}+bx+c$

$y=a\left(-{\frac {b}{2a}}\right)^{2}+b\left(-{\frac {b}{2a}}\right)+c\qquad {\textrm {Then~simplify\ldots }}$

$={\frac {ab^{2}}{4a^{2}}}-{\frac {b^{2}}{2a}}+c$

$={\frac {b^{2}}{4a}}-{\frac {2\cdot b^{2}}{2\cdot 2a}}+c\cdot {\frac {4a}{4a}}$

$={\frac {-b^{2}+4ac}{4a}}$

$=-{\frac {b^{2}-4ac}{4a}}=-{\frac {D}{4a}}$

Thus, the vertex is at point…

$\left(-{\frac {b}{2a}},-{\frac {D}{4a}}\right)$

Parabolas in the physical world

A bouncing ball captured with a stroboscopic flash at 25 images per second. Note that the ball becomes significantly non-spherical after each bounce, especially after the first. That, along with spin and air resistance, causes the curve swept out to deviate slightly from the expected perfect parabola

.

In nature, approximations of parabolas and paraboloids are found in many diverse situations. The most well-known instance of the parabola in the history of physics is the trajectory of a particle or body in motion under the influence of a uniform gravitational field without air resistance (for instance, a baseball flying through the air, neglecting air friction). The parabolic trajectory of projectiles was discovered experimentally by Galileo in the early seventeenth century, who performed experiments with balls rolling on inclined planes. The parabolic shape for projectiles was later proven mathematically by Isaac Newton. For objects extended in space, such as a diver jumping from a diving board, the object itself follows a complex motion as it rotates, but the center of mass of the object nevertheless forms a parabola. As in all cases in the physical world, the trajectory is always an approximation of a parabola. The presence of air resistance, for example, always distorts the shape, although at low speeds, the shape is a good approximation of a parabola. At higher speeds, such as in ballistics, the shape is highly distorted and does not resemble a parabola.

Parabolic shape formed by the surface of a Newtonian liquid under rotation

Another situation in which parabola may arise in nature is in two-body orbits, for example, of a small planetoid or other object under the influence of the gravitation of the sun. Such parabolic orbits are a special case that are rarely found in nature. Orbits that form a hyperbola or an ellipse are much more common. In fact, the parabolic orbit is the borderline case between those two types of orbit. An object following a parabolic orbit moves at the exact escape velocity of the object it is orbiting, while elliptical orbits are slower and hyperbolic orbits are faster.

Approximations of parabolas are also found in the shape of cables of suspension bridges. Freely hanging cables do not describe parabolas, but rather catenary curves. Under the influence of a uniform load (for example, the deck of bridge), however, the cable is deformed toward a parabola.

Paraboloids arise in several physical situations as well. The most well-known instance is the parabolic reflector, which is a mirror or similar reflective device that concentrates light or other forms of electromagnetic radiation to a common focal point. The principle of the parabolic reflector may have been discovered in the third century B.C.E. by the geometer Archimedes, who, according to a legend of debatable veracity, constructed parabolic mirrors to defend Syracuse against the Roman fleet, by concentrating the sun's rays to set fire to the decks of the Roman ships. The principle was applied to telescopes in the seventeenth century. Today, paraboloid reflectors can be commonly observed throughout much of the world in microwave and satellite dish antennas.

Paraboloids are also observed in the surface of a liquid confined to a container and rotated around the central axis. In this case, the centrifugal force causes the liquid to climb the walls of the container, forming a parabolic surface. This is the principle behind the liquid mirror telescope.

Aircraft used to create a weightless state for purposes of experimentation, such as NASA's “vomit comet,” follow a vertically parabolic trajectory for brief periods in order to trace the course of an object in free fall, which produces the same effect as zero gravity for most purposes.

See also

• Circle
• Conic section
• Hyperbola
• Ellipse

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240.

• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502.

• Research and Education Association. 1999. Math Made Nice-n-Easy Books #7: Trigonometric Identities & Equations, Straight Lines, Conic Sections. Piscataway, N.J.: Research & Education Association. ISBN 0878912061.

• Smith, Karen E. 2000. An Invitation to Algebraic Geometry. New York: Springer. ISBN 0387989803.

• Stillwell, John. 1998. Numbers and Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387982892.

External links

All links retrieved November 18, 2022.

• Eric W. Weisstein. Parabola. MathWorld.
• Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms.
• Archimedes Triangle and Squaring of Parabola at cut-the-knot.
• Two Tangents to Parabola at cut-the-knot.
• Parabola As Envelope of Straight Lines at cut-the-knot.
• Parabolic Mirror at cut-the-knot.
• Circumcircle of Three Parabola Tangents at cut-the-knot.
• Focal Properties of Parabola at cut-the-knot.
• Generation of parabola via Apollonius' mesh at cut-the-knot.
• Exploring Parabolas (JavaSketchpad).

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Parabola  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Parabola"

Note: Some restrictions may apply to use of individual images which are separately licensed.