Conic section

Types of conic sections.

In mathematics, a conic section (or just conic) is a curve that can be formed by intersecting a cone (more precisely, a right circular conical surface) with a plane. The conic sections were named and studied as long ago as 200 B.C.E., when Apollonius of Perga undertook a systematic study of their properties.

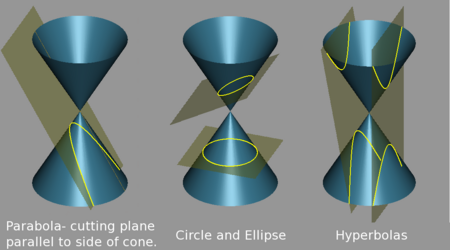
Two well-known conics are the circle and the ellipse. They arise when the intersection of the cone and plane is a closed curve. The circle is a special case of the ellipse in which the plane is perpendicular to the axis of the cone. If the plane is parallel to a generator line of the cone, the conic is called a parabola. Finally, if the intersection is an open curve and the plane is not parallel to generator lines of the cone, the figure is a hyperbola. (In this case the plane will intersect both halves of the cone, producing two separate curves, though often one is ignored.)

Conic sections are observed in the paths taken by celestial bodies. When two massive objects interact according to Newton's law of universal gravitation, their orbits are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas.

The study of conic sections is important not only for mathematics, physics, and astronomy, but also for a variety of engineering applications. The smoothness of conic sections is an important property for applications such as aerodynamics, where a smooth surface is needed to ensure laminar flow and prevent turbulence.

Table of conics, Cyclopaedia, 1728.

Degenerate cases

There are a number of degenerate cases, in which the plane passes through the apex of the cone. The intersection in these cases can be a straight line (when the plane is tangential to the surface of the cone); a point (when the angle between the plane and the axis of the cone is larger than this); or a pair of intersecting lines (when the angle is smaller). There is also a degenerate where the cone is a cylinder (the vertex is at infinity), which can produce two parallel lines.

Eccentricity

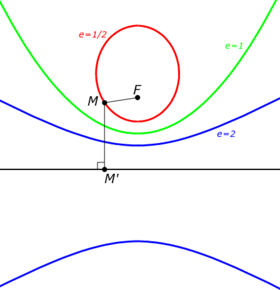
Ellipse (e=1/2), parabola (e=1) and hyperbola (e=2) with fixed focus F and directrix.

The four defining conditions above can be combined into one condition that depends on a fixed point F (the focus), a line L (the directrix) not containing F, and a nonnegative real number e (the eccentricity). The corresponding conic section consists of all points whose distance to F equals e times their distance to L. For 0 < e < 1 an ellipse is obtained; for e = 1, a parabola; and for e > 1, a hyperbola.

For an ellipse and a hyperbola, two focus-directrix combinations can be taken, each giving the same full ellipse or hyperbola. The distance from the center to the directrix is $a/e$ , where $a\$ is the semi-major axis of the ellipse, or the distance from the center to the tops of the hyperbola. The distance from the center to a focus is $ae\$ .

In the case of a circle, the eccentricity e = 0, and one can imagine the directrix to be infinitely far removed from the center. However, the statement that the circle consists of all points whose distance is e times the distance to L is not useful, because it yields zero times infinity.

The eccentricity of a conic section is thus a measure of how far it deviates from being circular.

For a given $a\$ , the closer $e\$ is to 1, the smaller is the semi-minor axis.

Cartesian coordinates

In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section, and all conic sections arise in this way. The equation will be of the form

Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\;

with

A\

,

B\

,

C\

not all zero.

then:

if $B^{2}-4AC<0\$ $B^{2}-4AC<0\$ , the equation represents an ellipse (unless the conic is degenerate, for example $x^{2}+y^{2}+10=0\$ $x^{2}+y^{2}+10=0\$ );
- if $A=C\$ and $B=0\$ , the equation represents a circle;
if $B^{2}-4AC=0\$ , the equation represents a parabola;
if $B^{2}-4AC>0\$ $B^{2}-4AC>0\$ , the equation represents a hyperbola;
- if we also have $A+C=0\$ , the equation represents a rectangular hyperbola.

Note that A and B are just polynomial coefficients, not the lengths of semi-major/minor axis as defined in the previous sections.

Through change of coordinates these equations can be put in standard forms:

Circle: $x^{2}+y^{2}=a^{2}\,$
Ellipse: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\$ , ${x^{2} \over b^{2}}+{y^{2} \over a^{2}}=1\$
Parabola: $y^{2}=4ax\,\$
Hyperbola: ${x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\$
Rectangular Hyperbola: $xy=c^{2}\$

Such forms will be symmetrical about the x-axis and for the circle, ellipse, and hyperbola, symmetrical about the y-axis.
The rectangular hyperbola however is only symmetrical about the lines $y=x\$ and $y=-x\$ . Therefore its inverse function is exactly the same as its original function.

These standard forms can be written as parametric equations,

Circle: $(a\cos \theta ,a\sin \theta )\,$ ,
Ellipse: $(a\cos \theta ,b\sin \theta )\,$ ,
Parabola: $(at^{2},2at)\,$ ,
Hyperbola: $(a\sec \theta ,b\tan \theta )\,$ or $(\pm a\cosh u,b\sinh u)\,$ .
Rectangular Hyperbola: $(ct,{c \over t})\,$

Homogeneous coordinates

In homogeneous coordinates a conic section can be represented as:

A_{1}x^{2}+A_{2}y^{2}+A_{3}z^{2}+2B_{1}xy+2B_{2}xz+2B_{3}yz=0.

Or in matrix notation

{\begin{bmatrix}x&y&z\end{bmatrix}}.{\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}.{\begin{bmatrix}x\\y\\z\end{bmatrix}}=0.

The matrix $M={\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}$ is called "the matrix of the conic section."

$\Delta =\det(M)=\det \left({\begin{bmatrix}A_{1}&B_{1}&B_{2}\\B_{1}&A_{2}&B_{3}\\B_{2}&B_{3}&A_{3}\end{bmatrix}}\right)$ is called the determinant of the conic section. If Δ = 0 then the conic section is said to be degenerate, this means that the conic section is in fact a union of two straight lines. A conic section that intersects itself is always degenerate, however not all degenerate conic sections intersect themselves; if they do not, they are straight lines.

For example, the conic section ${\begin{bmatrix}x&y&z\end{bmatrix}}.{\begin{bmatrix}1&0&0\\0&-1&0\\0&0&0\end{bmatrix}}.{\begin{bmatrix}x\\y\\z\end{bmatrix}}=0$ reduces to the union of two lines:

$\{x^{2}-y^{2}=0\}=\{(x+y)(x-y)=0\}=\{x+y=0\}\cup \{x-y=0\}$ .

Similarly, a conic section sometimes reduces to a (single) line:

$\{x^{2}+2xy+y^{2}=0\}=\{(x+y)^{2}=0\}=\{x+y=0\}\cup \{x+y=0\}=\{x+y=0\}$ .

$\delta =\det \left({\begin{bmatrix}A_{1}&B_{1}\\B_{1}&A_{2}\end{bmatrix}}\right)$ is called the discriminant of the conic section. If δ = 0 then the conic section is a parabola, if δ<0, it is an hyperbola and if δ>0, it is an ellipse. A conic section is a circle if δ>0 and A₁ = A₂, it is an rectangular hyperbola if δ<0 and A₁ = -A₂. It can be proven that in the complex projective plane CP² two conic sections have four points in common (if one accounts for multiplicity), so there are never more than 4 intersection points and there is always 1 intersection point (possibilities: 4 distinct intersection points, 2 singular intersection points and 1 double intersection points, 2 double intersection points, 1 singular intersection point and 1 with multiplicity 3, 1 intersection point with multiplicity 4). If there exists at least one intersection point with multiplicity > 1, then the two conic sections are said to be tangent. If there is only one intersection point, which has multiplicity 4, the two conic sections are said to be osculating.^[1]

Furthermore each straight line intersects each conic section twice. If the intersection point is double, the line is said to be tangent and it is called the tangent line. Because every straight line intersects a conic section twice, each conic section has two points at infinity (the intersection points with the line at infinity). If these points are real, the conic section must be a hyperbola, if they are imaginary conjugated, the conic section must be an ellipse, if the conic section has one double point at infinity it is a parabola. If the points at infinity are (1,i,0) and (1,-i,0), the conic section is a circle. If a conic section has one real and one imaginary point at infinity or it has two imaginary points that are not conjugated it is neither a parabola nor an ellipse nor a hyperbola.

Polar coordinates

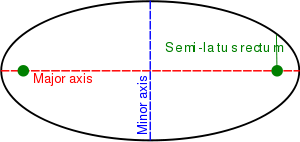
Semi-latus rectum in the case of an ellipse

The semi-latus rectum of a conic section, usually denoted l, is the distance from the single focus, or one of the two foci, to the conic section itself, measured along a line perpendicular to the major axis.

In polar coordinates, a conic section with one focus at the origin and, if any, the other on the x-axis, is given by the equation

r={l \over (1+e\cos \theta )}

.

As above, for e = 0, yields a circle, for 0 < e < 1 one obtains an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.

Applications

Conic sections are important in astronomy. The orbits of two massive objects that interact according to Newton's law of universal gravitation are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas.

Conic sections are always "smooth;" more precisely, they contain no inflection points. This is important for many applications, such as aerodynamics, where a smooth surface is required to ensure laminar flow and prevent turbulence.

In projective geometry, the conic sections in the projective plane are equivalent to each other up to projective transformations.

Notes

↑ E.J. Wilczynski, 1916, Some remarks on the historical development and the future prospects of the differential geometry of plane curves. Bull. Amer. Math. Soc. 22:317-329.

References
ISBN links support NWE through referral fees

Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240.
Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387986502.
Research and Education Association. 1999. Math Made Nice-n-Easy Books #7: Trigonometric Identities & Equations, Straight Lines, Conic Sections. Piscataway, N.J.: Research & Education Association. ISBN 0878912061.
Smith, Karen E. 2000. An Invitation to Algebraic Geometry. New York: Springer. ISBN 0387989803.
Stillwell, John. 1998. Numbers and Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387982892.
Stillwell, John. 2006. Yearning for the Impossible: The Surprising Truths of Mathematics. Wellesley, MA: A. K. Peters. ISBN 156881254X.

External links

All links retrieved March 20, 2017.

Conic sections
Eric W. Weisstein. Conic Section. MathWorld.
Occurrence of the conics.
Conics.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

Conic section ^history

The history of this article since it was imported to New World Encyclopedia:

History of "Conic section"

Note: Some restrictions may apply to use of individual images which are separately licensed.

[1] E.J. Wilczynski, 1916, Some remarks on the historical development and the future prospects of the differential geometry of plane curves. Bull. Amer. Math. Soc. 22:317-329.

[1]