Torque

Torque applied via an adjustable end wrench

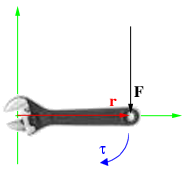
In physics, torque (or often called a moment) can informally be thought of as "rotational force" or "angular force" which causes a change in rotational motion. This force is defined by linear force multiplied by a radius. The symbol for torque is τ, the Greek letter tau. The concept of torque, also called moment or couple, originated with the work of Archimedes on levers. The rotational analogs of force, mass, and acceleration are torque, moment of inertia, and angular acceleration, respectively.

Relationship between force, torque, and momentum vectors in a rotating system

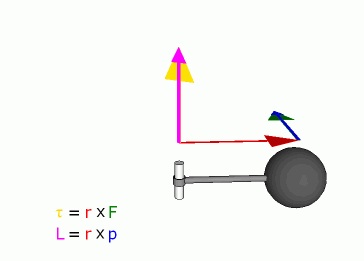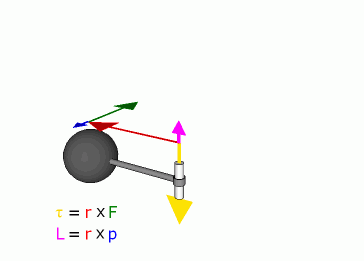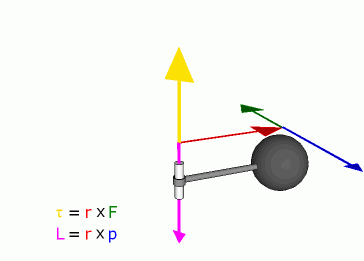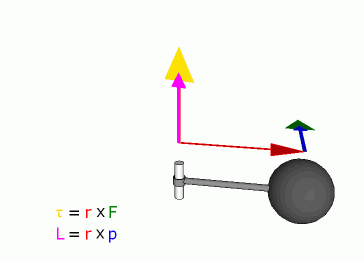
Example

In the case of a lever, the torque is equal to the force applied to the lever multiplied by its distance from the lever's fulcrum. For example, a force of three newtons applied two meters from the fulcrum exerts the same torque as one newton applied six meters from the fulcrum. This assumes the force is in a direction at right angles to the straight lever.

The direction of the torque can be determined by using the right hand rule: Using your right hand, curl your fingers in the direction of rotation, and stick your thumb out so it is aligned with the axis of rotation. Your thumb points in the direction of the torque vector.

Mathematically, the torque on a particle (which has the position r in some reference frame) can be defined as the cross product:

${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F}$

where

r is the particle's position vector

F is the force acting on the particle,

or, more generally, torque can be defined as the rate of change of angular momentum,

${\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$

where

L is the angular momentum vector

t stands for time.

As a consequence of either of these definitions, torque is a vector that points along the axis of the rotation it would tend to cause.

Units

Torque has dimensions of force times distance. The SI unit for torque is the newton meter (N m or N·m). In United States customary units, it is measured in pounds-feet (lb-ft) (or foot-pounds).

Although the order of "newton" and "meter" is mathematically interchangeable, the BIPM (Bureau International des Poids et Mesures) specifies that the order should be N·m not m·N.

The joule, which is the SI unit for energy or work, is also defined as 1 N·m, but this unit is not used for torque. Since energy can be thought of as the result of "force dot distance," energy is always a scalar whereas torque is "force cross distance" and so is a (pseudo) vector-valued quantity. Of course, the dimensional equivalence of these units is not simply a coincidence; a torque of 1 N·m applied through a full revolution will require an energy of exactly 2π joules. Mathematically,

$E=\tau \theta \$

where

E is the energy

τ is torque

θ is the angle moved, in radians.

Other non-SI units of torque include "pound-force-feet" or "foot-pounds-force" or "ounce-force-inches" or "meter-kilograms-force."

Special cases and other facts

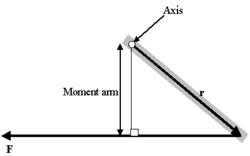
Moment arm formula

Moment arm diagram

A very useful special case, often given as the definition of torque in fields other than physics, is as follows:

${\boldsymbol {\tau }}=({\textrm {moment\ arm}})\times {\textrm {force}}$

The construction of the "moment arm" is shown in the figure below, along with the vectors r and F mentioned above. The problem with this definition is that it does not give the direction of the torque but only the magnitude, and hence it is difficult to use in three-dimensional cases. If the force is perpendicular to the displacement vector r, the moment arm will be equal to the distance to the center, and torque will be a maximum for the given force. The equation for the magnitude of a torque arising from a perpendicular force:

${\boldsymbol {T}}=({\textrm {distance\ to\ center}})\times {\textrm {force}}$

For example, if a person places a force of 10 N on a spanner that is 0.5 m long, the torque will be 5 N·m, assuming that the person pulls the spanner by applying force perpendicular to the spanner.

Force at an angle

If a force of magnitude F is at an angle θ from the displacement arm of length r (and within the plane perpendicular to the rotation axis), then from the definition of cross product, the magnitude of the torque arising is:

${\boldsymbol {\tau }}=rF\sin \theta$

Static equilibrium

For an object to be in static equilibrium, not only must the sum of the forces be zero, but also the sum of the torques (moments) about any point. For a two-dimensional situation with horizontal and vertical forces, the sum of the forces requirement is two equations: ΣH = 0 and ΣV = 0, and the torque a third equation: Στ = 0. That is, to solve statically determinate equilibrium problems in two-dimensions, we use three equations.

Torque as a function of time

The torque caused by the two opposing forces F_g and -F_g causes a change in the angular momentum L in the direction of that torque. This causes the top to precess.

Torque is the time-derivative of angular momentum, just as force is the time derivative of linear momentum:

${\boldsymbol {\tau }}={\mathrm {d} \mathbf {L} \over \mathrm {d} t}\,\!$

where

L is angular momentum.

Angular momentum on a rigid body can be written in terms of its moment of inertia ${\boldsymbol {I}}\,\!$ and its angular velocity ${\boldsymbol {\omega }}$:

$\mathbf {L} =I\,{\boldsymbol {\omega }}\,\!$

so if ${\boldsymbol {I}}\,\!$ is constant,

${\boldsymbol {\tau }}=I{\mathrm {d} {\boldsymbol {\omega }} \over \mathrm {d} t}=I{\boldsymbol {\alpha }}\,\!$

where α is angular acceleration, a quantity usually measured in radians per second squared.

Machine torque

Torque is part of the basic specification of an engine: the power output of an engine is expressed as its torque multiplied by its rotational speed. Internal-combustion engines produce useful torque only over a limited range of rotational speeds (typically from around 1,000–6,000 rpm for a small car). The varying torque output over that range can be measured with a dynamometer, and shown as a torque curve. The peak of that torque curve usually occurs somewhat below the overall power peak. The torque peak cannot, by definition, appear at higher rpm than the power peak.

Understanding the relationship between torque, power and engine speed is vital in automotive engineering, concerned as it is with transmitting power from the engine through the drive train to the wheels. Typically power is a function of torque and engine speed. The gearing of the drive train must be chosen appropriately to make the most of the motor's torque characteristics.

Steam engines and electric motors tend to produce maximum torque close to zero rpm, with the torque diminishing as rotational speed rises (due to increasing friction and other constraints). Therefore, these types of engines usually have quite different types of drivetrains from internal combustion engines.

Torque is also the easiest way to explain mechanical advantage in just about every simple machine.

Relationship between torque, power and energy

If a force is allowed to act through a distance, it is doing mechanical work. Similarly, if torque is allowed to act through a rotational distance, it is doing work. Power is the work per unit time. However, time and rotational distance are related by the angular speed where each revolution results in the circumference of the circle being travelled by the force that is generating the torque. This means that torque that is causing the angular speed to increase is doing work and the generated power may be calculated as:

${\mbox{Power}}={\mbox{torque}}\times {\mbox{angular speed}}\,$

On the right hand side, this is a scalar product of two vectors, giving a scalar on the left hand side of the equation. Mathematically, the equation may be rearranged to compute torque for a given power output. However in practice there is no direct way to measure power whereas torque and angular speed can be measured directly.

In practice, this relationship can be observed in power stations which are connected to a large electrical power grid. In such an arrangement, the generator's angular speed is fixed by the grid's frequency, and the power output of the plant is determined by the torque applied to the generator's axis of rotation.

Consistent units must be used. For metric SI units power is watts, torque is newton-meters and angular speed is radians per second (not rpm and not revolutions per second).

Also, the unit newton-meter is dimensionally equivalent to the joule, which is the unit of energy. However, in the case of torque, the unit is assigned to a vector, whereas for energy, it is assigned to a scalar.

Conversion to other units

For different units of power, torque, or angular speed, a conversion factor must be inserted into the equation. Also, if rotational speed (revolutions per time) is used in place of angular speed (radians per time), a conversion factor of $2\pi$ must be added because there are $2\pi$ radians in a revolution:

${\mbox{Power}}={\mbox{torque}}\times 2\pi \times {\mbox{rotational speed}}\,$,

where rotational speed is in revolutions per unit time.

Useful formula in SI units:

${\mbox{Power (kW)}}={\frac {{\mbox{torque (Nm)}}\times \pi \times {\mbox{rotational speed (rpm)}}}{30000}}$

Some people (e.g. American automotive engineers) use horsepower (imperial mechanical) for power, foot-pounds (lbf·ft) for torque and rpm's (revolutions per minute) for angular speed. This results in the formula changing to:

${\mbox{Power (hp)}}\approx {\frac {{\mbox{torque(lbf}}\cdot {\mbox{ft)}}\times {\mbox{rotational speed (rpm)}}}{5252}}$

This conversion factor is approximate because the transcendental number π appears in it; a more precise value is 5252.113 122 032 55... It also changes with the definition of the horsepower, of course; for example, using the metric horsepower, it becomes ~5180.

Use of other units (e.g. BTU/h for power) would require a different custom conversion factor.

Derivation

For a rotating object, the linear distance covered at the circumference in a radian of rotation is the product of the radius with the angular speed. That is: linear speed = radius x angular speed. By definition, linear distance=linear speed x time = radius x angular speed x time.

By the definition of torque: torque=force x radius. We can rearrange this to determine force=torque/radius. These two values can be substituted into the definition of power:

${\mbox{power}}={\frac {{\mbox{force}}\times {\mbox{linear distance}}}{\mbox{time}}}={\frac {\left({\frac {\mbox{torque}}{r}}\right)\times (r\times {\mbox{angular speed}}\times t)}{t}}={\mbox{torque}}\times {\mbox{angular speed}}$

The radius r and time t have dropped out of the equation. However angular speed must be in radians, by the assumed direct relationship between linear speed and angular speed at the beginning of the derivation. If the rotational speed is measured in revolutions per unit of time, the linear speed and distance are increased proportionately by $2\pi$ in the above derivation to give:

${\mbox{power}}={\mbox{torque}}\times 2\pi \times {\mbox{rotational speed}}\,$

If torque is in lbf·ft and rotational speed in revolutions per minute, the above equation gives power in ft·lbf/min. The horsepower form of the equation is then derived by applying the conversion factor 33,000 ft·lbf/min per horsepower:

${\mbox{power}}={\mbox{torque }}\times \ 2\pi \ \times {\mbox{ rotational speed}}\cdot {\frac {{\mbox{ft}}\cdot {\mbox{lbf}}}{\mbox{min}}}\times {\frac {\mbox{horsepower}}{33000\cdot {\frac {{\mbox{ft }}\cdot {\mbox{ lbf}}}{\mbox{min}}}}}\approx {\frac {{\mbox{torque}}\times {\mbox{RPM}}}{5252}}$

because $5252.113...={\frac {33,000}{2\pi }}\,$.

See also

• Angular momentum
• Mechanical work
• Moment (physics)
• Statics
• Torque wrench
• Torsion

References

ISBN links support NWE through referral fees

• Serway, Raymond A., and John W. Jewett. 2004. Physics for Scientists and Engineers. 6th ed. Brooks/Cole. ISBN 0534408427

• Tipler, Paul. 2004. Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics. 5th ed. W. H. Freeman. ISBN 0716708094.

External links

All links retrieved May 1, 2023.

• An interactive simulation of torque

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Torque  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Torque"

Note: Some restrictions may apply to use of individual images which are separately licensed.