Frequency

Sinusoidal waves of various frequencies; the bottom waves have higher frequencies than those above. The horizontal axis represents time.

Frequency is a measure of the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency. The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency. Frequency is an important parameter in our understanding of waves and of wavelike phenomena, such as electromagnetism.

Definition and units

For cyclical processes, such as rotation, oscillations, or waves, frequency is defined as a number of cycles, or periods, per unit time. In physics and engineering disciplines, such as optics, acoustics, and radio, frequency is usually denoted by a Latin letter f or by a Greek letter ν (nu).

In SI units, the unit of frequency is hertz (Hz), named after the German physicist Heinrich Hertz. For example, 1 Hz means that an event repeats once per second, 2 Hz is twice per second, and so on. This unit was originally called one cycle per second (cps), which is still sometimes used. Heart rate and musical tempo are measured in beats per minute (BPM). Frequency of rotation is often expressed as a number of revolutions per minute (rpm). BPM and rpm values must be divided by 60 to obtain the corresponding value in Hz: thus, 60 BPM translates into 1 Hz.

The period is usually denoted as T, and is the reciprocal of the frequency f:

$T={\frac {1}{f}}.$

The SI (as well as English) unit for period is the second (s).

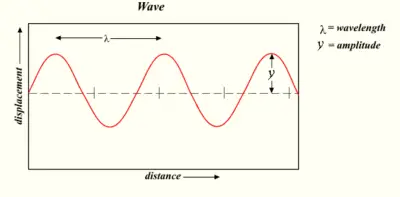
Some parameters of a wave

A wave can be described mathematically using a series of parameters including its wavelength, wavenumber, period, frequency, and amplitude.

The wavelength (denoted as $\lambda$) is the distance between two successive crests (or troughs). It is generally measured on the metric scale (in meters, centimeters, and so on). For the optical part of the electromagnetic spectrum, wavelength is commonly measured in nanometers (one nanometer equals a billionth of a meter).

A wavenumber, $k$, can be associated with the wavelength by the relation

$k={\frac {2\pi }{\lambda }}$.

The period, $T$, of a wave is the time taken for a wave oscillation to go through one complete cycle (one crest and one trough).

The frequency $f$ (also denoted as $\nu$) is the number of periods per unit time. Frequency is usually measured in hertz (Hz), which corresponds to the number of cycles per second. The frequency and period of a wave are reciprocals of each other. Thus their mathematical relationship is:

$f={\frac {1}{T}}$.

One complete cycle of a wave can be said to have an "angular displacement" of 2$\pi$ radians—in other words, one cycle is completed and another is about to begin. Thus there is another parameter called angular frequency (or angular speed), $\omega$. It is measured as the number of radians per unit time (radians per second) at a fixed position. Angular frequency is related to the frequency by the equation:

$\omega =2\pi f={\frac {2\pi }{T}}$

The amplitude of a wave (commonly denoted as A or another letter) is a measure of the maximum disturbance in the medium during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave. The units for measuring amplitude depend on the type of wave. Waves on a string have an amplitude expressed in terms of distance (meters); sound waves, as pressure (in pascals); and electromagnetic waves, as the amplitude of the electric field (in volts/meter). The amplitude may be constant, in which case the wave is called a continuous wave (c.w.), or it may vary with time or position. The form of variation of amplitude is called the envelope of the wave.

There are two types of velocity associated with a wave: phase velocity and group velocity. Phase velocity gives the rate at which the wave propagates. It is calculated by the equation:

$v_{p}={\frac {\omega }{k}}=\lambda f$

Group velocity gives the rate at which information can be transmitted by the wave. In scientific terms, it is the velocity at which variations in the wave's amplitude propagate through space. Group velocity is given by the equation:

$v_{g}={\frac {\partial \omega }{\partial k}}$

Relationship between frequency and wavelength

Frequency has an inverse relationship to the concept of wavelength: simply, frequency is inversely proportional to wavelength λ (lambda). The frequency f is equal to the speed v of the wave divided by the wavelength λ of the wave:

$f={\frac {v}{\lambda }}.$

In the special case of electromagnetic waves moving through a vacuum, then v = c₀ , where c₀ is the speed of light in a vacuum, and this expression becomes:

$f={\frac {c_{0}}{\lambda }}.$

When waves from a monochromatic source travel from one medium to another, their frequency remains exactly the same—only their wavelength and speed change.

Measurement

By timing

To calculate the frequency of an event, the number of occurrences of the event within a fixed time interval are counted, and then divided by the length of the time interval.

In experimental work (for example, calculating the frequency of an oscillating pendulum) it is more accurate to measure the time taken for a fixed number of occurrences, rather than the number of occurrences within a fixed time. The latter method introduces—if N is the number of counted occurrences—a random error between zero and one count, so on average half a count, causing an biased underestimation of f by ½ f / (N + ½) in its expected value. In the first method, which is more accurate, frequency is still calculated by dividing the number of occurrences by the time interval; however it is the number of occurrences that is fixed, not the time interval.

An alternative method to calculate frequency is to measure the time between two consecutive occurrences of the event (the period T) and then compute the frequency f as the reciprocal of this time:

$f={\frac {1}{T}}.$

A more accurate measurement can be obtained by taking many cycles into account and averaging the periods between each.

By stroboscope effect, or frequency beats

In case when the frequency is so high that counting is difficult or impossible with the available means, another method is used, based on a source (such as a laser, a tuning fork, or a waveform generator) of a known reference frequency f₀, that must be tunable or very close to the measured frequency f. Both the observed frequency and the reference frequency are simultaneously produced, and frequency beats are observed at a much lower frequency Δf, which can be measured by counting. This is sometimes referred to as a stroboscope effect. The unknown frequency is then found from $f=f_{0}\pm \Delta f$.

Examples

• In music and acoustics, the frequency of the standard pitch A above middle C on a piano is usually defined as 440 Hz, that is, 440 cycles per second and known as concert pitch, to which an orchestra tunes.
• A baby can hear tones with oscillations up to approximately 20,000 Hz, but these frequencies become more difficult to hear as people age.
• In Europe, Africa, Australia, Southern South America, most of Asia, and Russia, the frequency of the alternating current in household electrical outlets is 50 Hz (close to the tone G), whereas in North America and Northern South America, the frequency of the alternating current is 60 Hz (between the tones B♭ and B—that is, a minor third above the European frequency). The frequency of the 'hum' in an audio recording can show where the recording was made—in countries utilizing the European, or the American grid frequency.
• Visible light from deep red to violet has frequencies of 430 to 750 THz.

Period versus frequency

As a matter of convenience, longer and slower waves, such as ocean surface waves, tend to be described by wave period rather than frequency. Short and fast waves, like audio and radio, are usually described by their frequency instead of period. These commonly used conversions are listed below:

Frequency	1 mHz (10-3)	1 Hz (100)	1 kHz (103)	1 MHz (106)	1 GHz (109)	1 THz (1012)
Period (time)	1 ks (103)	1 s (100)	1 ms (10-3)	1 µs (10-6)	1 ns (10-9)	1 ps (10-12)

Other types of frequency

• Angular frequency ω is defined as the rate of change in the orientation angle (during rotation), or in the phase of a sinusoidal waveform (e.g. in oscillations and waves):

$\omega =2\pi f\,$.

Angular frequency is measured in radians per second (rad/s).

• Spatial frequency is analogous to temporal frequency, but the time axis is replaced by one or more spatial displacement axes.
• Wavenumber is the spatial analogue of angular frequency. In case of more than one space dimension, wavenumber is a vector quantity.

See also

• Electromagnetic spectrum
• Electronics
• Wave
• Wavelength

References

ISBN links support NWE through referral fees

• French, A. P. Vibrations and Waves. The M.I.T. Introductory Physics Series. New York: Norton, 1971. ISBN 0393099245
• Pain, H. J. The Physics of Vibrations and Waves. Chichester: John Wiley, 2005. ISBN 978-0470012963
• Tipler, Paul Allen, and Gene Mosca. Physics for Scientists and Engineers, 5th ed. New York: W.H. Freeman, 2003. ISBN 0716743892
• Wilson, Jerry D., and Anthony J. Buffa. College Physics. Upper Saddle River, NJ: Prentice Hall, 2003. ISBN 0130676446

External links

All links retrieved April 11, 2024.

• Conversion: period, cycle duration, periodic time to frequency
• Keyboard frequencies = naming of notes - The English and American system versus the German system
• Teaching resource for 14-16yrs on sound including frequency

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Frequency  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Frequency"

Note: Some restrictions may apply to use of individual images which are separately licensed.