Wave

A wave just before breaking at Manhattan Beach, California.

A wave is a disturbance that propagates through space in a regular pattern, often involving the transfer of energy. When thinking about waves, a person tends to recall ocean waves or ripples on a pond. Scientists have found that sound and light (electromagnetic radiation) can also be described in terms of wave motion. Sound involves mechanical waves that propagate as vibrations through a medium, such as a solid, liquid, or gas. By contrast, light can travel through a vacuum, that is, without a medium. In addition, the movement of subatomic particles also has wavelike properties. Thus a wide range of physical phenomena can be understood in terms of wave motion.

Waves can be represented by simple harmonic motion.

Examples

Examples of waves include:

Ocean surface waves, which are perturbations that propagate through water.
Sound waves, which are mechanical waves that propagate through air, liquids, or solids. In common usage, sound waves have frequencies that are detectable by the human ear. Scientists, however, include other similar vibratory phenomena in the general category of "sound," even when they lie outside the range of human hearing. It should be noted that although these waves travel and transfer energy from one point to another, there is little or no permanent displacement of the particles of the medium. Rather, the particles of the medium simply oscillate around fixed positions.
Electromagnetic radiation, which is constituted of radio waves (including microwaves), infrared rays, visible light, ultraviolet rays, X rays, and gamma rays. The various forms of electromagnetic radiation differ in their frequencies (and wavelengths), but they share other properties. They can propagate through a vacuum, traveling at a speed of approximately three hundred thousand kilometers/second. According to the quantum mechanical model, these forms of radiation exhibit the properties of particles as well as waves. The "particles" are thought to consist of packets of energy known as photons.

Moreover, Albert Einstein's theory of General Relativity predicts the existence of gravitational waves, which are fluctuations in the gravitational field. These waves, however, have yet to be observed empirically.

Characteristics

Surface waves in water

Periodic waves are characterized by crests (highs) and troughs (lows). If the waves remain in one place, such as the vibrations of a violin string, they are called standing waves. If the waves are moving, they are called traveling waves.

Waves are often classified as either longitudinal or transverse. Transverse waves are those with vibrations perpendicular to the direction of propagation of the wave; examples include waves on a string and electromagnetic waves. Longitudinal waves are those with vibrations parallel to the direction of propagation of the wave. Most sound waves are longitudinal waves, where the air is both compressed and rarified in the direction of movement of the traveling wave.

A = At deep water.
B = At shallow water. The circular movement of a surface particle becomes elliptical with decreasing depth.
1 = Progression of wave
2 = Crest
3 = Trough

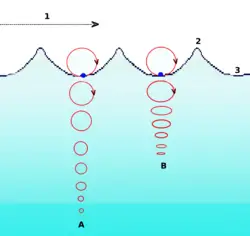
Ripples on the surface of a pond are actually a combination of transverse and longitudinal waves, and the points on the surface follow orbital paths. Thus, when an object bobs up and down on ripples in a pond, it experiences an orbital trajectory.

All waves exhibit certain types of behavior depending on the situation, as follows:

Reflection – the change of direction of waves when they hit a reflective surface.
Refraction – the change of direction of waves when they enter a new medium.
Interference – the superposition of two (or more) waves that contact each other, producing a new wave pattern.
Diffraction – the bending, spreading, and interference of waves when they pass by an obstruction or go through a narrow gap.
Dispersion – the splitting up of waves that have several components of different frequencies.
Rectilinear propagation – the movement of waves in straight lines.

Thus, by understanding the concept and behavior of waves, we can explain the properties of sound, electromagnetic radiation, subatomic particles, and so forth.

Polarization

A wave is said to be "polarized" when it oscillates in only one direction. The polarization of a transverse wave (such as light) indicates that the oscillations occur in a single plane perpendicular to the direction of travel. Longitudinal waves, such as sound waves, do not exhibit polarization, because for these waves the direction of oscillation is along the direction of travel. A wave can be polarized by using a device called a "polarizing filter."

Parameters of a wave

A wave can be described mathematically using a series of parameters including its amplitude, wavelength, wavenumber, period, and frequency.

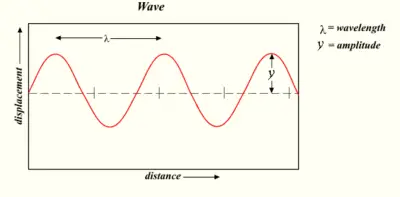
The amplitude of a wave (commonly denoted as A or another letter) is a measure of the maximum disturbance in the medium during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave. The units for measuring amplitude depend on the type of wave. Waves on a string have an amplitude expressed in terms of distance (meters); sound waves, as pressure (in pascals); and electromagnetic waves, as the amplitude of the electric field (in volts/meter). The amplitude may be constant, in which case the wave is called a continuous wave (c.w.), or it may vary with time or position. The form of variation of amplitude is called the envelope of the wave.

The wavelength (denoted as $\lambda$ ) is the distance between two successive crests (or troughs). It is generally measured on the metric scale (in meters, centimeters, and so on). For the optical part of the electromagnetic spectrum, wavelength is commonly measured in nanometers (one nanometer equals a billionth of a meter).

A wavenumber, $k$ , can be associated with the wavelength by the relation

k={\frac {2\pi }{\lambda }}

.

The period, $T$ , of a wave is the time taken for a wave oscillation to go through one complete cycle (one crest and one trough). The frequency $f$ (also denoted as $\nu$ ) is the number of periods per unit time. Frequency is usually measured in hertz (Hz), which corresponds to the number of cycles per second. The frequency and period of a wave are reciprocals of each other. Thus their mathematical relationship is:

f={\frac {1}{T}}

.

One complete cycle of a wave can be said to have an "angular displacement" of 2 $\pi$ radians—in other words, one cycle is completed and another is about to begin. Thus there is another parameter called angular frequency (or angular speed), $\omega$ . It is measured as the number of radians per unit time (radians per second) at a fixed position. Angular frequency is related to the frequency by the equation:

\omega =2\pi f={\frac {2\pi }{T}}

There are two types of velocity associated with a wave: phase velocity and group velocity. Phase velocity gives the rate at which the wave propagates. It is calculated by the equation:

v_{p}={\frac {\omega }{k}}=\lambda f

Group velocity gives the rate at which information can be transmitted by the wave. In scientific terms, it is the velocity at which variations in the wave's amplitude propagate through space. Group velocity is given by the equation:

v_{g}={\frac {\partial \omega }{\partial k}}

Interference based on phases of waves

Interference pattern produced with a Michelson interferometer. Bright bands are the result of constructive interference, and the dark bands are the result of destructive interference.

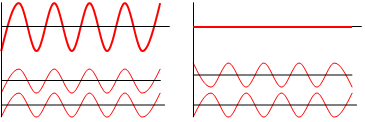
Consider two waves that have the same wavelength (or frequency) and amplitude $A$ , and they are superimposed on each other such that they are "in phase"—that is, the crests and troughs of one wave overlap the crests and troughs of the other, respectively. Then the resultant waveform will have an amplitude of $2A$ . This is known as constructive interference.

On the other hand, if the same two waves are 180° out of phase when superimposed (that is, the crests of one wave exactly overlap the troughs of the other), the resultant waveform will have an amplitude of zero. This is known as destructive interference.

Constructive and destructive interference are illustrated below.

combined waveform
wave 1
wave 2
	Two waves in phase	Two waves 180° out of phase

Transmission medium

The medium that carries a wave is called the transmission medium. It can be classified into one or more of the following categories:

A linear medium, if the amplitudes of different waves at any particular point in the medium can be added.
A bounded medium, if the medium is finite in extent; otherwise, the medium is called an unbounded medium.
A uniform medium, if the physical properties of the medium are the same in different parts of the medium.
An isotropic medium, if the physical properties of the medium are the same in different directions.

Mathematics of specific cases

Propagation through strings

The speed (v) of a wave traveling along a string is directly proportional to the square root of the tension (T) over the linear density (ρ):

v={\sqrt {\frac {T}{\rho }}}.

Traveling waves

Traveling waves have a disturbance (amplitude $u$ ) that varies with both time ( $t$ ) and distance ( $z$ ). This can be expressed mathematically as:

u=A(z,t)\cos(\omega t-kz+\phi )\,

where $A(z,t)$ is the amplitude envelope of the wave, $k$ is the wave number, and $\phi$ is the phase of the wave.

The wave equation

The wave equation is a differential equation that describes how a harmonic wave changes over time. The equation has slightly different forms, depending on how the wave is transmitted and the medium it is traveling through. For a one-dimensional wave traveling down a rope along the $x$ -axis with velocity ( $v$ ) and amplitude ( $u$ ) (which generally depends on both x and t), the wave equation is:

{\frac {1}{v^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {\partial ^{2}u}{\partial x^{2}}}.\

In three dimensions, the equation becomes:

{\frac {1}{v^{2}}}{\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}

.

It should be noted that the velocity ( $v$ ) depends on both the type of wave and the medium through which it is being transmitted.

A general solution for the wave equation in one dimension was given by French physicist-mathematician Jean Le Rond d'Alembert (1717-1783). It is

u(x,t)=F(x-vt)+G(x+vt).\

This can be viewed as two pulses travelling down a taut rope in opposite directions; F in the +x direction, and G in the -x direction. If we substitute for x above, replacing it with directions x, y, z, we then can describe a wave propagating in three dimensions.

In quantum mechanics, the Schrödinger equation describes the wavelike behavior of subatomic particles. Solutions of this equation are wave functions that can be used to describe the probability density of a particle. Quantum mechanics also describes particle properties that other waves (such as light and sound) have on the atomic and subatomic scales.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

Wave ^history
Interference ^history

The history of this article since it was imported to New World Encyclopedia:

History of "Wave"

Note: Some restrictions may apply to use of individual images which are separately licensed.