Orbital

This diagram shows: (a) (on left side) the order in which orbitals are filled with electrons, for different elements in the periodic table; (b) (on upper right) shapes of some atomic orbitals; and (c) (on lower right) shapes of some molecular orbitals.

In physics and chemistry, an atomic orbital is a region in which an electron may be found within a single atom. Likewise, a molecular orbital is a region in which an electron may be found in a molecule. In general, atomic orbitals combine to form molecular orbitals.

In the classical model, electrons were thought to orbit the atomic nucleus much like planets orbiting the Sun (or moths orbiting speedily around a lamp). As the concept of an electron shifted from a solid particle to an entity with both wave-like and particle-like properties, it became clear that the electron does not have a well-defined position or orbit within the atom. Consequently, the electron was thought of as a "cloud" distributed around a nucleus, like a large atmosphere around a tiny planet. For this reason, the term orbit was replaced by the term orbital.

Atomic orbitals

Explaining the distribution and behavior of electrons within an atom was one of the driving forces behind the development of quantum mechanics. In quantum mechanics, atomic orbitals are the quantum states (or discrete energy states) that electrons surrounding an atomic nucleus may exist in. Each atomic orbital has a characteristic energy level and a particular distribution of electron density. An orbital can be described as a "wave function" of an electron in an atom, and the shape of an orbital indicates the probability of locating the electron within a particular region of the atom.

Orbitals in hydrogen-like atoms

The simplest atomic orbitals are those that occur in an atom with a single electron, such as the hydrogen atom. An atom of any other element ionized down to a single electron is very similar to hydrogen, and the orbitals take similar forms.

For atoms with two or more electrons, the governing equations can be solved only by using the methods of iterative approximation. Orbitals of multi-electron atoms are qualitatively similar to those of hydrogen, and in the simplest models, they are taken to have the same form. For more rigorous and precise analysis, the numerical approximations must be used.

A given (hydrogen-like) atomic orbital is identified by unique values of three quantum numbers:

• the principal quantum number n
• the angular momentum (or azimuthal) quantum number l
• the magnetic quantum number m_l.

The rules restricting the values of the quantum numbers, and their energies (see below), explain the electron configuration of the atoms and the periodic table.

The stationary states (quantum states) of hydrogen-like atoms are its atomic orbital. In general, however, an electron's behavior is not fully described by a single orbital. Electron states are best represented by time-dependent combinations (linear combinations) of multiple orbitals.

The quantum number n first appeared in the Bohr model. It determines, among other things, the distance of the electron from the nucleus; all electrons with the same value of n lay at the same distance. Modern quantum mechanics confirms that these orbitals are closely related. For this reason, orbitals with the same value of n are said to comprise a "shell." Orbitals with the same value of n and the same value of l are even more closely related and are said to comprise a "subshell."

Values of the quantum numbers

An atomic orbital is uniquely identified by the values of the three quantum numbers n, l, and m_l. Each set of these three quantum numbers corresponds to exactly one orbital, but the quantum numbers occur in only certain combinations of values. The rules governing the possible values of the quantum numbers are as follows:

• The principal quantum number n is always a positive integer: 1, 2, 3, … In principle, it can be any positive integer, but for reasons discussed below, large numbers are seldom encountered. Generally, an atom has several orbitals associated with each value of n. Orbitals associated with the same value of n are said to lie in the same shell.

• The azimuthal quantum number $\ell$ is a non-negative integer: 0, 1, 2, … Within a shell where n is some integer n₀, $\ell$ ranges across all (integer) values satisfying the relation $0\leq \ell \leq n_{0}-1$. For instance, the shell represented by n = 1 has only orbitals with $\ell =0$, and the shell n = 2 shell has only orbitals with $\ell =0$, and $\ell =1$. The set of orbitals associated with a particular value of $\ell$ are said to form the same subshell.'.

• The magnetic quantum number $m_{\ell }$ is also always an integer. Within a subshell where $\ell$ is some integer $\ell _{0}$, $m_{\ell }$ ranges as: $-\ell _{0}\leq m_{\ell }\leq \ell _{0}$.

The above rules are summarized in the following table. Each cell represents a subshell, and lists the values of $m_{\ell }$ available in that subshell. Empty cells represent subshells that do not exist.

	$l=0$	1	2	3	4	...
$n=1$	$m_{l}=0$
2	0	-1, 0, 1
3	0	-1, 0, 1	-2, -1, 0, 1, 2
4	0	-1, 0, 1	-2, -1, 0, 1, 2	-3, -2, -1, 0, 1, 2, 3
5	0	-1, 0, 1	-2, -1, 0, 1, 2	-3, -2, -1, 0, 1, 2, 3	-4, -3, -2 -1, 0, 1, 2, 3, 4
...	...	...	...	...	...	...

Subshells are usually identified by their $n$- and $\ell$-values. $n$ is represented by its numerical value, but $\ell$ is represented by a letter as follows: 0 is represented by 's', 1 by 'p', 2 by 'd', 3 by 'f', and 4 by 'g'. For instance, one may speak of the subshell with $n=2$ and $\ell =0$ as a "2s subshell."

Orbital names

The first four orbital names (s, p, d, f) are derived from the quality of their spectroscopic lines: sharp, principal, diffuse, and fundamental. Subsequent orbitals are named in alphabetical order (g, h, …).

Orbital names take the following format:

$X\,\mathrm {type} ^{y}\$

where X is the energy level corresponding to the "shell" number principal quantum number $n\$; type is a lower-case letter denoting the shape or "subshell" of the orbital, corresponding to the angular momentum quantum number (or azimuthal quantum number) $\ell \$; and y is the number of electrons in that orbital.

For example, the orbital $1s^{2}$ (pronounced "one s two") has two electrons in the lowest energy level (n = 1), with an angular momentum quantum number of l = 0. In some cases, the principal quantum number is designated by a letter. For n = 1, 2, 3, 4, 5, … , the associated letters are K, L, M, N, O, … , respectively.

Shapes of atomic orbitals

The shapes of the first five atomic orbitals. The colors show the wavefunction phase.

Any discussion of the shapes of electron orbitals is necessarily imprecise, because a given electron, regardless of which orbital it occupies, can at any moment be found at any distance from the nucleus and in any direction due to the uncertainty principle.

However, the electron is much more likely to be found in certain regions of the atom than in others. Given this, a boundary surface can be drawn so that the electron has a high probability to be found anywhere within the surface, and all regions outside the surface have low values. The precise placement of the surface is arbitrary, but any reasonably compact determination must follow a pattern specified by the behavior of $\psi ^{2}$, the square of the wavefunction. This boundary surface is what is meant when the "shape" of an orbital is mentioned.

Generally speaking, the number $n$ determines the size and energy of the orbital: as $n$ increases, the size of the orbital increases.

Also in general terms, $\ell$ determines an orbital's shape, and $m_{\ell }$ its orientation. However, since some orbitals are described by equations in complex numbers, the shape sometimes depends on $m_{\ell }$ as well.

The single $s$-orbitals ($\ell =0$) are shaped like spheres. For n=1 the sphere is "solid" (it is most dense at the center and fades exponentially outwardly), but for n=2 or more, each single s-orbital is composed of spherically symmetric surfaces which are nested shells (i.e., the "wave-structure" is radial, following a sinusoidal radial component as well). The $s$-orbitals for all n numbers are the only orbitals with an anti-node (a region of high wave function density) at the center of the nucleus. All other orbitals (p, d, f, etc.) have angular momentum, and thus avoid the nucleus (having a wave node at the nucleus).

The three $p$-orbitals have the form of two ellipsoids with a point of tangency at the nucleus, (sometimes referred to as a dumbbell). The three $p$-orbitals in each shell are oriented at right angles to each other, as determined by their respective values of $m_{\ell }$.

Four of the five $d$-orbitals look similar, each with four pear-shaped balls, each ball tangent to two others, and the centers of all four lying in one plane, between a pair of axes. Three of these planes are the $xy$-, $xz$-, and $yz$-planes, and the fourth has the centers on the $x$ and $y$ axes. The fifth and final $d$-orbital consists of three regions of high probability density: a torus with two pear-shaped regions placed symmetrically on its $z$ axis.

There are seven $f$-orbitals, each with shapes more complex than those of the $d$-orbitals.

The shapes of atomic orbitals in one-electron atom are related to 3-dimensional spherical harmonics.

Table of atomic orbitals

The following table shows all orbital configurations up to 7s. It covers the simple electronic configurations for all elements of the periodic table up to Ununbium (element 112), with the exception of Lawrencium (element 103), which would require a 7p orbital.

	s (l=0)	p (l=1)	d (l=2)	f (l=3)
n=1
n=2
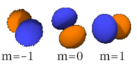
n=3
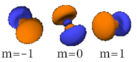
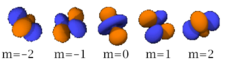
n=4
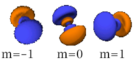
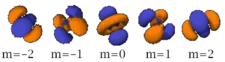
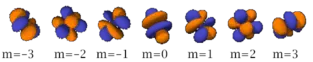
n=5
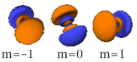
n=6
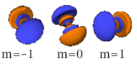
n=7

Orbital energy

In atoms with a single electron (essentially the hydrogen atom), the energy of an orbital (and, consequently, of any electrons in the orbital) is determined exclusively by $n$. The $n=1$ orbital has the lowest possible energy in the atom. Each successively higher value of $n$ has a higher level of energy, but the difference decreases as $n$ increases. For high values of $n$, the energy level becomes so high that the electron can easily escape from the atom.

In atoms with multiple electrons, the energy of an electron depends not only on the intrinsic properties of its orbital, but also on its interactions with the other electrons. These interactions depend on the detail of its spatial probability distribution, and so the energy levels of orbitals depend not only on $n$ but also on $\ell$. Higher values of $\ell$ are associated with higher values of energy; for instance, the 2p state is higher than the 2s state. When $\ell$ = 2, the increase in energy of the orbital becomes so large as to push the energy of orbital above the energy of the s-orbital in the next higher shell; when $\ell$ = 3 the energy is pushed into the shell two steps higher.

The energy order of the first 24 subshells is given in the following table. Each cell represents a subshell with $n$ and $\ell$ given by its row and column indices, respectively. The number in the cell is the subshell's position in the sequence. Empty cells represent subshells that do not exist.

	$s$	$p$	$d$	$f$	$g$
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26
7	16	19	23	27	32
8	20	24	28	33	38

Electron placement and the periodic table

Several rules govern the placement of electrons in orbitals (electron configuration). The first dictates that no two electrons in an atom may have the same set of values of all quantum numbers (this is the Pauli exclusion principle). These quantum numbers include the three that define orbitals, as well as s, or spin quantum number. Thus, two electrons may occupy a single orbital, so long as they have different values of $s$. However, only two electrons, because of their spin, can be associated with each orbital.

Additionally, an electron always tries to occupy the lowest possible energy state. It is possible for it to occupy any orbital so long as it does not violate the Pauli exclusion principle, but if lower-energy orbitals are available, this condition is unstable. The electron will eventually lose energy (by releasing a photon) and drop into the lower orbital. Thus, electrons fill orbitals in the order specified by the energy sequence given above.

This behavior is responsible for the structure of the periodic table. The table may be divided into several rows (called 'periods'), numbered starting with 1 at the top. The presently known elements occupy seven periods. If a certain period has number $i$, it consists of elements whose outermost electrons fall in the $i$th shell.

The periodic table may also be divided into several numbered rectangular 'blocks'. The elements belonging to a given block have this common feature: their highest-energy electrons all belong to the same $\ell$-state (but the $n$ associated with that $\ell$-state depends upon the period). For instance, the leftmost two columns constitute the 's-block'. The outermost electrons of Li and Be respectively belong to the 2s subshell, and those of Na and Mg to the 3s subshell.

The number of electrons in a neutral atom increases with the atomic number. The electrons in the outermost shell, or valence electrons, tend to be responsible for an element's chemical behavior. Elements that contain the same number of valence electrons can be grouped together and display similar chemical properties.

Formal quantum mechanical definition of atomic orbitals

In quantum mechanics, the state of an atom, that is, the eigenstates of the atomic Hamiltonian, is expanded into linear combinations of anti-symmetrized products (Slater determinants) of one-electron functions. The spatial components of these one-electron functions are called atomic orbitals. (When their spin component is included, they are called atomic spin orbitals.)

In atomic physics, the atomic spectral lines correspond to transitions (quantum leaps) between quantum states of an atom. These states are labeled by a set of quantum numbers summarized in the term symbol and usually associated to particular electron configurations, i.e., by occupations schemes of atomic orbitals (e.g., $1s^{2}2s^{2}2p^{6}\$ for the ground state of neon—term symbol: ${}^{1}\!S_{0}\$).

This notation means that the corresponding Slater determinants have a clear higher weight in the configuration interaction expansion. The atomic orbital concept is therefore a key concept for visualizing the excitation process associated to a given transition. For example, one can say for a given transition that it corresponds to the excitation of an electron from an occupied orbital to a given unoccupied orbital. Nevertheless one has to keep in mind that electrons are fermions ruled by Pauli exclusion principle and cannot be distinguished from the other electrons in the atom. Moreover, it sometimes happens that the configuration interaction expansion converges very slowly and that one cannot speak about simple one-determinantal wave function at all. This is the case when electron correlation is large.

Fundamentally, an atomic orbital is a one-electron wavefunction.

Molecular orbitals

Complete set of molecular orbitals of acetylene.

Most methods in computational chemistry today start by calculating the molecular orbitals (MOs) of the system. A molecular orbital describes the behavior of one electron in the electric field generated by the nuclei and some average distribution of the other electrons. If two electrons occupy the same orbital, the Pauli principle demands that they have opposite spin.

Qualitative discussion

For an imprecise but qualitatively useful discussion of molecular structure, molecular orbitals can be obtained by the "linear combination of atomic orbitals molecular orbital method." In this approach, the molecular orbitals are expressed as linear combinations of atomic orbitals, as if each atom were on its own.

Molecular orbitals were first introduced by Friedrich Hund and Robert S. Mulliken in 1927 and 1928. The linear combination of atomic orbitals approximation for molecular orbitals was introduced in 1929 by Sir John Lennard-Jones.. His ground-breaking paper showed how to derive the electronic structures of the fluorine and oxygen molecules from quantum principles. This qualitative approach to molecular orbital theory formed part of the beginning of modern quantum chemistry.

Some properties:

• The number of molecular orbitals is equal to the number the atomic orbitals included in the linear expansion.
• If the molecule has some symmetry, the degenerate atomic orbitals (with the same atomic energy) are grouped in linear combinations (called symmetry adapted atomic orbitals (SO)) which belong to the representation of the symmetry group, so the wave functions that describe the group is known as symmetry-adapted linear combinations (SALC).
• The number of molecular orbitals belonging to one group representation is equal to the number of symmetry-adapted atomic orbitals belonging to this representation.
• Within a particular representation, the symmetry-adapted atomic orbitals mix more if their atomic energy levels are closer.

Examples

H₂

H₂ 1sσ bonding molecular orbital

H₂ 1sσ* antibonding molecular orbital

As a simple example, consider the hydrogen molecule, H₂, with the two atoms labeled H' and H." The lowest-energy atomic orbitals, 1s' and 1s," do not transform according to the symmetries of the molecule. However, the following symmetry-adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

The symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. Because the H₂ molecule has two electrons, they can both go in the bonding orbital, making the system lower in energy (and hence more stable) than two free hydrogen atoms. This is called a covalent bond. The bond order is equal to the number of bonding electrons minus the number of antibonding electrons, all divided by 2. In this example, there are two electrons in the bonding orbital and none in the antibonding orbital; the bond order is 1, and there is a single bond between the two hydrogen atoms.

He₂

On the other hand, consider the hypothetical molecule of He₂, with the atoms labeled He' and He. Again, the lowest-energy atomic orbitals, 1s' and 1s," do not transform according to the symmetries of the molecule, while the following symmetry-adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

Similar to the molecule H₂, the symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. However, in its neutral ground state, each helium atom contains two electrons in its 1s orbital, combining for a total of four electrons. Two electrons fill the lower energy bonding orbital, while the remaining two fill the higher energy antibonding orbital. Thus, the resulting electron density around the molecule does not support the formation of a bond (sigma bond) between the two atoms, and the molecule therefore is not formed. Another way of looking at it is that there are two bonding electrons and two antibonding electrons; therefore, the bond order is 0 and no bond exists.

Ionic bonds

When the energy difference between the atomic orbitals of two atoms is quite large, one atom's orbitals contribute almost entirely to the bonding orbitals, and the other's almost entirely to the antibonding orbitals. Thus, the situation is effectively that some electrons have been transferred from one atom to the other. This is called a (predominantly) ionic bond.

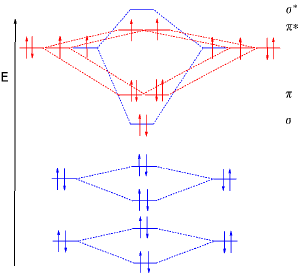
Molecular orbital diagrams

For more complicated molecules, the wave mechanics approach loses utility in a qualitative understanding of bonding (although is still necessary for a quantitative approach). The qualitative approach of MO uses a molecular orbital diagram. In this type of diagram, the molecular orbitals are represented by horizontal lines; the higher a line, the higher the energy of the orbital, and degenerate orbitals are placed on the same level with a space between them. Then, the electrons to be placed in the molecular orbitals are slotted in one by one, keeping in mind the Pauli exclusion principle and Hund's rule of maximum multiplicity (only two electrons per orbital (opposite spins); have as many unpaired electrons on one energy level as possible before starting to pair them).

The hardest part is to construct the MO diagram. For a simple molecule such as H₂, we draw the diagram like this:

__ σ^*

__ σ

The σ indicates a sigma bonding orbital, while σ^* indicates a sigma antibonding orbital. We know that the diagram looks like this because we know that two s orbitals will interact to form a σ bonding orbital and a σ antibonding orbital.

Now if one considers N₂, one realizes that the two nitrogen atoms each have a filled 1s orbital, a filled 2s orbital, and three half-filled 2p orbitals. The 1s orbitals, being inner shell, do not interact (or, equivalently, they are not valence electrons, as explained by valence bond theory).

The two 2s orbitals do, however, interact to create a σ_s orbital and a σ_s^* orbital:

__ σ_s^*

__ σ_s

If we assume that the interatomic axis joining the two N atoms is the z axis, we find that the two 2p_z orbitals are able to overlap lobe-to-lobe to create a sigma bond. The two 2p_x and two 2p_y orbitals, lying perpendicular to the z axis, interact to create four pi orbitals (two bonding, two antibonding).

Finally, we must decide on the order of the orbitals. The 2s orbitals, since they were initially of lowest energy, interact to create the lowest-energy orbitals. The 2p sigma bonds must be stronger than the pi bonds, so we expect the σ_p orbital to be lower than the π_p orbital. However, this is not the case, primarily because of hybridization mixing the 2s and 2p orbitals. However, we do have the expected order for the σ_p^* and π_p^* orbitals:

___ σ_p^*

___ ___ π_p^*

___ σ_p

___ ___ π_p

___ σ_s^*

___ σ_s

As promised, there are 8 orbitals, the sum of the number of atomic orbitals (4+4) which combined to create the molecular orbitals. The total number of electrons is then 10 (five valence electrons from each atom). Two go into the σ_s orbital; two go into the σ_s^* orbital; four into the two π_p orbitals, and two go into the σ_p orbital.

The sigma bond order is the total number of electrons in sigma bonding orbitals (4), minus the total number of electrons in sigma bonding orbitals (2) , all over 2 giving (4-2)/2 = 1. There is the similar pi bond order, giving (4 - 0)/2. Adding these together gives the total bond order. In this case the lowest two orbitals "cancel out"; there is one sigma bond and two pi bonds. Dinitrogen therefore has a triple bond.

Finally, we know that diatomic nitrogen is diamagnetic since there are no unpaired electrons in the diagram.

This diagram, however, is not applicable to molecules of oxygen, fluorine, and neon. Because of the higher electronegativity of these elements, the formation of hybrid orbitals is less important, and thus we get the "expected" order of energy levels:

___ σ_p^*

___ ___ π_p^*

___ ___ π_p

___ σ_p

___ σ_s^*

___ σ_s

The observation that the formation of hybrid orbitals is much less energetically favorable for smaller, more electronegative atoms (which are found in the first row) is due to the energy difference in the atom between the 2s and 2p orbitals. This energy difference increases from left to right along a row and from top to bottom down a column of the periodic table, so is highest for fluorine, which has the lowest mixing of s and p in the MOs. Mixing is most important when the energy difference is small.

If we were working with diatomic oxygen, we would use this MO diagram. In this case, there would be 12 electrons to place into molecular orbitals; the first ten go into the five orbitals of lowest energy; the last two, however, occupy separate π_p^* orbitals. The bond order is reduced to 2 since this is an antibonding orbital; also, the two unpaired electrons make liquid oxygen paramagnetic, which is not explained by the localized electron model.

MO diagram for the oxygen molecule

A further observation is that molecular orbital theory explains why the dicarbon molecule, C₂, does not contain a quadruple bond in its ground state although it would complete the octet - there are four bonding orbitals, but the top three cannot be occupied before one antibonding orbital is occupied.

More quantitative approach

To obtain quantitative values for the molecular energy levels, one needs to have molecular orbitals which are such that the configuration interaction (CI) expansion converges fast towards the full CI limit. The most common method to obtain such functions is the Hartree-Fock method, which expresses the molecular orbitals as eigenfunctions of the Fock operator. One usually solves this problem by expanding the molecular orbitals as linear combinations of gaussian functions centered on the atomic nuclei (see linear combination of atomic orbitals and basis set (chemistry)). The equation for the coefficients of these linear combinations is a generalized eigenvalue equation known as the Roothaan equations which are in fact a particular representation of the Hartree-Fock equation.

Simple accounts often suggest that experimental molecular orbital energies can be obtained by the methods of ultraviolet photoelectron spectroscopy for valence orbitals and X-ray photoelectron spectroscopy for core orbitals. This, however, is incorrect as these experiments measure the ionization energy, the difference in energy between the molecule and one of the ions resulting from the removal of one electron. Ionization energies are linked approximately to orbital energies by Koopmans' theorem. While the agreement between these two values can be close for some molecules, it can be poor in other cases.

HOMO/LUMO

HOMO and LUMO are acronyms for highest occupied molecular orbital and lowest unoccupied molecular orbital, respectively. The difference between the energies of the HOMO and LUMO, termed the band gap can sometimes serve as a measure of the excitability of the molecule: the smaller the energy, the more easily it will be excited.

The HOMO level is to organic semiconductors what the valence band is to inorganic semiconductors. The same analogy exists between the LUMO level and the conduction band. The energy difference between the HOMO and LUMO level is regarded as band gap energy.

When the molecule forms a dimer or an aggregate, the proximity of the orbitals of the different molecules induce a splitting of the HOMO and LUMO energy levels. This splitting produces vibrational sublevels, each of which has its own energy, slightly different from that of another.

There are as many vibrational sublevels as there are molecules that interact together. When there are enough molecules influencing each other (such as in an aggregate), there are so many sublevels that we no longer perceive their discrete nature: they form a continuum. We no longer consider energy levels, but energy bands.

See also

• Atom
• Electron
• Hydrogen
• Molecule
• Quantum chemistry

References

ISBN links support NWE through referral fees

• Chang, Raymond. 2006. Chemistry, 9th ed. New York: McGraw-Hill. ISBN 0073221031.
• Daintith, J. 2004. Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 0198609183.
• Kutzelnigg, Werner, "Friedrich Hund and Chemistry" (on the occasion of Hund's 100th birthday), Angewandte Chemie 35 (1996): 573-586.
• Pope, Martin, and Charles E. Swenberg. 1999. Electronic Processes in Organic Crystals and Polymers, 2nd ed. New York: Oxford University Press. ISBN 0195129636.
• Tipler, Paul, and Ralph Llewellyn. 2003. Modern Physics, 4th ed. New York: W.H. Freeman. ISBN 0716743450.

External links

All links retrieved November 17, 2022.

• Atomic Orbitals.
• The Orbitron: A gallery of atomic orbitals and molecular orbitals on the WWW. from 1s to 7g.
• Grand Orbital Table.
• David Manthey's Atomic Orbitals.
• Hydrogen Atom Orbital Viewer. (Java applet.)
• Molecular Orbital Viewer. (Java applet, for the hydrogen molecular ion.)

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Atomic_orbital  ^history
• Molecular_orbital  ^history
• HOMO/LUMO  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Orbital"

Note: Some restrictions may apply to use of individual images which are separately licensed.