Difference between revisions of "Trigonometry" - New World Encyclopedia
David Oben (talk | contribs) (→Applications of trigonometry: removal of broken image) |
(imported latest version of article from Wikipedia) |
||
| Line 1: | Line 1: | ||
| − | {{ | + | {{pp-move-vandalism|small=yes}} |
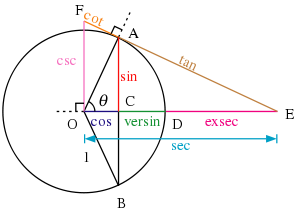
| + | [[Image:STS-114 Steve Robinson on Canadarm2.jpg|thumb|300px|The [[Canadarm2]] robotic manipulator on the [[International Space Station]] is operated by controlling the angles of its joints. Calculating the final position of the astronaut at the end of the arm requires repeated use of the trigonometric functions of those angles.]][[Image:Circle-trig6.svg|300px|thumb|right|All of the [[trigonometric function]]s of an angle ''θ'' can be constructed geometrically in terms of a unit circle centered at ''O''.]] | ||
| + | |||
| + | '''Trigonometry''' (from [[Greek language|Greek]] ''Τριγωνομετρία'' "tri = three" + "gon = angle" + "metr[y] = to measure") is a branch of [[mathematics]] that deals with [[triangle (geometry)|triangle]]s, particularly those [[plane (mathematics)|plane]] triangles in which one [[angle]] has 90 degrees ('''right triangles'''). Trigonometry deals with relationships between the sides and the angles of triangles and with the [[trigonometric functions]], which describe those relationships. | ||
| + | |||
| + | Trigonometry has applications in both [[pure mathematics]] and in [[applied mathematics]], where it is essential in many branches of science and technology. It is usually taught in [[secondary schools]] either as a separate course or as part of a [[precalculus]] course. Trigonometry is informally called "trig" or "trigo". | ||
| + | |||
| + | A branch of trigonometry, called [[spherical trigonometry]], studies triangles on [[sphere]]s, and is important in [[astronomy]] and [[navigation]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== History == | == History == | ||
| − | [[Image: | + | [[Image:Table of Trigonometry, Cyclopaedia, Volume 2.jpg|thumb|right|250px|Table of Trigonometry, 1728 ''[[Cyclopaedia]]'']] |
| − | {{main|History of | + | {{main|History of trigonometry}} |
| + | {{Unreferencedsection|date=July 2008}} | ||
| + | Trigonometry was developed for use in [[sailing]] as a navigation method used with [[astronomy]].<ref>{{cite book|author=Christopher M. Linton|title=From Eudoxus to Einstein: A History of porn|publisher=Cambridge University Press|year=2004}}</ref> The origins of trigonometry can be traced to the civilizations of [[ancient Egypt]], [[Mesopotamia]] and the [[Indus Valley Civilization|Indus Valley]] ([[India]]), more than 4000 years ago.{{Fact|date=February 2007}} The common practice of measuring angles in degrees, minutes and seconds comes from the [[Babylonia]]n's [[sexagesimal|base sixty]] system of numeration. | ||
| − | + | The first recorded use of trigonometry came from the [[Greek mathematics|Hellenistic mathematician]] [[Hipparchus]][http://www.math.rutgers.edu/~cherlin/History/Papers2000/hunt.html] circa 150 B.C.E., who compiled a trigonometric [[Mathematical table|table]] using the [[sine]] for solving triangles. [[Ptolemy]] further developed trigonometric calculations circa 100 C.E.. | |
| − | The | + | The ancient [[Sinhalese people|Sinhalese]] in [[Sri Lanka]], when constructing reservoirs in the [[Anuradhapura]] kingdom, used trigonometry to calculate the [[gradient]] of the water flow. Archeological research also provides evidence of trigonometry used in other unique hydrological structures dating back to 4 B.C.E..{{Fact|date=July 2008}} |
| − | The | + | The Indian mathematician [[Aryabhata]] in 499, gave tables of half chords which are now known as [[sine]] tables, along with [[cosine]] tables. He used ''zya'' for sine, ''kotizya'' for [[cosine]], and ''otkram zya'' for inverse sine, and also introduced the [[versine]]. Another Indian mathematician, [[Brahmagupta]] in 628, used an [[interpolation]] formula to compute values of sines, up to the second order of the [[Isaac Newton|Newton]]-[[James Stirling (mathematician)|Stirling]] interpolation formula. |
| − | + | In the 10th century, the Persian mathematician and astronomer [[Abul Wáfa]] introduced the [[tangent|tangent function]] and improved methods of calculating trigonometry tables. He established the angle addition identities, e.g. sin (''a'' + ''b''), and discovered the sine formula for spherical geometry: | |
| − | + | :<math>\frac{\sin A}{\sin a} = \frac{\sin B}{\sin b} = \frac{\sin C}{\sin c}.</math> | |
| − | + | Also in the late 10th and early 11th centuries, the Egyptian astronomer [[Ibn Yunus]] performed many careful trigonometric calculations and demonstrated the formula | |
| − | + | :<math>\cos a \cos b = \frac{\cos(a+b) + \cos(a-b)}{2}.</math>. | |
| − | |||
| − | |||
[[Persian people|Persian]] [[Islamic mathematics|mathematician]] [[Omar Khayyám]] (1048-1131) combined trigonometry and [[approximation theory]] to provide methods of solving algebraic equations by geometrical means. Khayyam solved the cubic equation <math>x^3 + 200 x = 20 x^2 + 2000</math> and found a positive root of this cubic by considering the intersection of a rectangular [[hyperbola]] and a circle. An approximate numerical solution was then found by interpolation in trigonometric tables. | [[Persian people|Persian]] [[Islamic mathematics|mathematician]] [[Omar Khayyám]] (1048-1131) combined trigonometry and [[approximation theory]] to provide methods of solving algebraic equations by geometrical means. Khayyam solved the cubic equation <math>x^3 + 200 x = 20 x^2 + 2000</math> and found a positive root of this cubic by considering the intersection of a rectangular [[hyperbola]] and a circle. An approximate numerical solution was then found by interpolation in trigonometric tables. | ||
| Line 34: | Line 36: | ||
In the 14th century, Persian mathematician [[al-Kashi]] and [[Timurid]] mathematician [[Ulugh Beg]] (grandson of [[Timur]]) produced tables of trigonometric functions as part of their studies of astronomy. | In the 14th century, Persian mathematician [[al-Kashi]] and [[Timurid]] mathematician [[Ulugh Beg]] (grandson of [[Timur]]) produced tables of trigonometric functions as part of their studies of astronomy. | ||
| − | The mathematician [[Bartholemaeus Pitiscus]] published an influential work on trigonometry in 1595 which may have coined the word "trigonometry. | + | The mathematician [[Bartholemaeus Pitiscus]] published an influential work on trigonometry in 1595 which may have coined the word "trigonometry" itself. |
==Overview== | ==Overview== | ||
| − | [[Image:TrigonometryTriangle.svg|thumb|240px|In this right triangle: sin'' | + | [[Image:TrigonometryTriangle.svg|thumb|240px|In this right triangle: {{nowrap|1= sin ''A'' = ''a''/''c'';}} {{nowrap|1= cos ''A'' = ''b''/''c'';}} {{nowrap|1= tan ''A'' = ''a''/''b''.}}]] |
| − | + | If one [[angle]] of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are [[complementary angles]]. The [[shape]] of a right triangle is completely determined, up to [[similarity (geometry)|similarity]], by the angles. This means that once one of the other angles is known, the [[ratio]]s of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following [[trigonometric function]]s of the known angle ''A'', where ''a'', '' b'' and ''c'' refer to the lengths of the sides in the accompanying figure: | |
*The '''sine''' function (sin), defined as the ratio of the side opposite the angle to the hypotenuse. | *The '''sine''' function (sin), defined as the ratio of the side opposite the angle to the hypotenuse. | ||
| − | :<math>\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}</math> | + | :<math>\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}=\frac{a}{\,c\,}\,.</math> |
*The '''cosine''' function (cos), defined as the ratio of the adjacent leg to the hypotenuse. | *The '''cosine''' function (cos), defined as the ratio of the adjacent leg to the hypotenuse. | ||
| − | :<math>\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}</math> | + | :<math>\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{b}{\,c\,}\,.</math> |
*The '''tangent''' function (tan), defined as the ratio of the opposite leg to the adjacent leg. | *The '''tangent''' function (tan), defined as the ratio of the opposite leg to the adjacent leg. | ||
| − | :<math>\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{\sin A}{\cos A}</math> | + | :<math>\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{a}{\,b\,}=\frac{\sin A}{\cos A}\,.</math> |
| − | The ''' | + | The '''hypotenuse''' is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle ''A''. The '''adjacent leg''' is the other side that is adjacent to angle ''A''. The '''opposite side''' is the side that is opposite to angle ''A''. The terms '''perpendicular''' and '''base''' are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under [[#Mnemonics|Mnemonics]]). |
The [[Multiplicative inverse|reciprocals]] of these functions are named the '''cosecant''' (csc or cosec), '''secant''' (sec) and '''cotangent''' (cot), respectively. The [[Inverse trigonometric function|inverse functions]] are called the '''arcsine''', '''arccosine''', and '''arctangent''', respectively. There are arithmetic relations between these functions, which are known as [[trigonometric identities]]. | The [[Multiplicative inverse|reciprocals]] of these functions are named the '''cosecant''' (csc or cosec), '''secant''' (sec) and '''cotangent''' (cot), respectively. The [[Inverse trigonometric function|inverse functions]] are called the '''arcsine''', '''arccosine''', and '''arctangent''', respectively. There are arithmetic relations between these functions, which are known as [[trigonometric identities]]. | ||
| Line 54: | Line 56: | ||
===Extending the definitions=== | ===Extending the definitions=== | ||
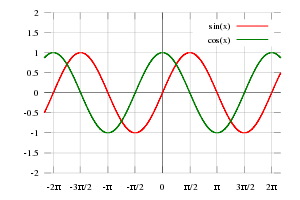
| − | [[Image:Sine cosine plot.svg|300px|right|thumb|Graphs of the functions sin'' | + | [[Image:Sine cosine plot.svg|300px|right|thumb|Graphs of the functions sin(''x'') and cos(''x''), where the angle ''x'' is measured in radians.]] |
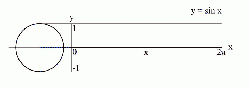
| − | The above definitions apply to angles between 0 and 90 degrees (0 and π/2 [[radian]]s) only. Using the [[unit circle]], one | + | [[Image:sin drawing process.gif|250px|thumb|right|Graphing process of ''y'' = sin(''x'') using a unit circle.]] |
| + | [[Image:tan drawing process.gif|250px|thumb|right|Graphing process of ''y'' = tan(''x'') using a unit circle.]] | ||
| + | [[Image:csc drawing process.gif|250px|thumb|right|Graphing process of ''y'' = csc(''x'') using a unit circle.]] | ||
| + | The above definitions apply to angles between 0 and 90 degrees (0 and π/2 [[radian]]s) only. Using the [[unit circle]], one can extend them to all positive and negative arguments (see [[trigonometric function]]). The trigonometric functions are [[periodic function|periodic]], with a period of 360 degrees or 2π radians. That means their values repeat at those intervals. | ||
The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from [[calculus]] and [[infinite series]]. With these definitions the trigonometric functions can be defined for [[complex number]]s. The complex function '''cis''' is particularly useful | The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from [[calculus]] and [[infinite series]]. With these definitions the trigonometric functions can be defined for [[complex number]]s. The complex function '''cis''' is particularly useful | ||
| − | : <math>\operatorname{cis} | + | : <math>\operatorname{cis}\,x = \cos x + i\sin x \! = e^{ix}. </math> |
See [[Euler's formula|Euler's]] and [[De Moivre's formula|De Moivre's]] formulas. | See [[Euler's formula|Euler's]] and [[De Moivre's formula|De Moivre's]] formulas. | ||
| Line 65: | Line 70: | ||
===Mnemonics=== | ===Mnemonics=== | ||
<!-- Note: | <!-- Note: | ||
| − | One mnemonic is enough, and the others were absolutely ridiculous. DO NOT ADD IN YOUR OWN MNEMONICS, or other ridiculous ones such as "Sex on | + | One mnemonic is enough, and the others were absolutely ridiculous. DO NOT ADD IN YOUR OWN MNEMONICS, or other ridiculous ones such as "Sex on holidays Comes after having Tons of alchohol" etcetera. but add in mnemonics for things other than the Sin, Cos and Tan functions, such as I have. toby engel |
| − | Such edits DO NOT improve the article, but add a method of obfuscation and in some cases, subversive vandalism through a "learning mnemonic, | + | Such edits DO NOT improve the article, but add a method of obfuscation and in some cases, subversive vandalism through a "learning mnemonic", and WILL BE REVERTED.—> |
| + | <!-- If you decide to change the title of the header, please fix the redirect at [[SOH-CAH-TOA]], replacing the text after the pound sign with the title of the new section. Thank you! —> | ||
| − | Students often | + | Students often use [[mnemonic]]s to remember facts and relationships in trigonometry. For example, the ''sine'', ''cosine'', and ''tangent'' ratios in a right triangle can be remembered by representing them as strings of letters, as in SOH-CAH-TOA. |
| − | === | + | :'''S'''ine = '''O'''pposite ÷ '''H'''ypotenuse |
| − | + | :'''C'''osine = '''A'''djacent ÷ '''H'''ypotenuse | |
| − | + | :'''T'''angent = '''O'''pposite ÷ '''A'''djacent | |
| − | + | ||
| − | + | Alternatively, one can devise sentences which consist of words beginning with the letters to be remembered. For example, to recall that Tan = Opposite/Adjacent, the letters T-O-A must be remembered. Any memorable phrase constructed of words beginning with the letters T-O-A will serve. | |
| − | + | ||
| − | + | It is of [[ethnographic]] interest to note that the mnemonic TOA-CAH-SOH can be translated in the local [[Singaporean]] [[Hokkien]] dialect to 'big-legged woman', serving as an additional learning aid for students in [[Singapore]]<ref>{{cite web| title = Trigonometry - My Grandmother Also Can Do This!| url=http://www.exampaper.com.sg/questions/e-maths/trigonometry-my-grandmother-also-can-do-this| accessdate = 2008-08-30}} Diary of a Private O Level Maths Tutor in Singapore</ref>. | |
| − | + | ||
| − | + | Another type of mnemonic describes facts in a simple, memorable way, such as "Plus to the right, minus to the left; positive height, negative depth," which refers to trigonometric functions generated by a revolving line. | |
===Calculating trigonometric functions=== | ===Calculating trigonometric functions=== | ||
| Line 88: | Line 94: | ||
==Applications of trigonometry == | ==Applications of trigonometry == | ||
| − | |||
{{main|Uses of trigonometry}} | {{main|Uses of trigonometry}} | ||
| Line 94: | Line 99: | ||
Fields which make use of trigonometry or trigonometric functions include [[astronomy]] (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence [[navigation]] (on the oceans, in aircraft, and in space), [[music theory]], [[acoustics]], [[optics]], analysis of financial markets, [[electronics]], [[probability theory]], [[statistics]], [[biology]], [[medical imaging]] ([[CAT scan]]s and [[ultrasound]]), [[pharmacy]], [[chemistry]], [[number theory]] (and hence [[cryptology]]), [[seismology]], [[meteorology]], [[oceanography]], many [[physical science]]s, land [[surveying]] and [[geodesy]], [[architecture]], [[phonetics]], [[economics]], [[electrical engineering]], [[mechanical engineering]], [[civil engineering]], [[computer graphics]], [[cartography]], [[crystallography]] and [[game development]]. | Fields which make use of trigonometry or trigonometric functions include [[astronomy]] (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence [[navigation]] (on the oceans, in aircraft, and in space), [[music theory]], [[acoustics]], [[optics]], analysis of financial markets, [[electronics]], [[probability theory]], [[statistics]], [[biology]], [[medical imaging]] ([[CAT scan]]s and [[ultrasound]]), [[pharmacy]], [[chemistry]], [[number theory]] (and hence [[cryptology]]), [[seismology]], [[meteorology]], [[oceanography]], many [[physical science]]s, land [[surveying]] and [[geodesy]], [[architecture]], [[phonetics]], [[economics]], [[electrical engineering]], [[mechanical engineering]], [[civil engineering]], [[computer graphics]], [[cartography]], [[crystallography]] and [[game development]]. | ||
| + | |||
| + | [[Image:Frieberger drum marine sextant.jpg|thumb|250px|Marine [[sextant]]s like this are used to measure the angle of the sun or stars with respect to the horizon. Using trigonometry and a [[marine chronometer]], the position of the ship can then be determined from several such measurements.]] | ||
==Common formulae== | ==Common formulae== | ||
| Line 104: | Line 111: | ||
====Pythagorean identities==== | ====Pythagorean identities==== | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | \sin^2 | + | \sin^2 \alpha + \cos^2 \alpha = 1 \\ |
| − | \tan^2 | + | \tan^2 \alpha + 1 = \sec^2 \alpha \\ |
| − | 1+\cot^2 | + | 1+\cot^2 \alpha = \csc^2 \alpha \end{align}</math> |
====Sum and product identities==== | ====Sum and product identities==== | ||
=====Sum to product:===== | =====Sum to product:===== | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | \sin | + | \sin \alpha \pm \sin \beta &= 2\sin \left( \frac{\alpha \pm \beta}{2}\right)\cos \left(\frac{\alpha \mp \beta}{2} \right)\\ |
| − | \cos | + | \cos \alpha + \cos \beta &= 2\cos \left(\frac{\alpha + \beta}{2} \right)\cos \left(\frac{\alpha - \beta}{2}\right)\\ |
| − | \cos | + | \cos \alpha - \cos \beta &= -2\sin \left(\frac{\alpha + \beta}{2} \right) \sin \left(\frac{\alpha - \beta}{2}\right) |
\end{align}</math> | \end{align}</math> | ||
| − | =====Product to sum:===== | + | =====Product to sum<ref>{{cite web|url=http://mathworld.wolfram.com/TrigonometricAdditionFormulas.html|title=Trigonometric Addition Formulas|author=Weisstein, Eric W|publisher=Wolfram MathWorld}}</ref>:===== |
:<math>\begin{align} | :<math>\begin{align} | ||
| − | \cos | + | \cos \alpha \,\cos \beta &= \frac{1}{2}[\cos(\alpha - \beta) + \cos (\alpha + \beta)]\\ |
| − | \sin | + | \sin \alpha \,\sin \beta &= \frac{1}{2}[\cos(\alpha - \beta) - \cos (\alpha + \beta)]\\ |
| − | \cos | + | \cos \alpha \,\sin \beta &= \frac{1}{2}[\sin(\alpha + \beta) - \sin (\alpha - \beta)]\\ |
| − | \sin | + | \sin \alpha \,\cos \beta &= \frac{1}{2}[\sin(\alpha + \beta) + \sin (\alpha - \beta)] |
\end{align}</math> | \end{align}</math> | ||
| − | ==== | + | =====Sine, cosine, and tangent of a sum===== |
| + | |||
| + | Detailed, diagramed proofs of the first two of these formulas | ||
| + | are available<br /> for download as a four-page PDF document | ||
| + | at [[Image:Sine Cos Proofs.pdf]]. | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| − | \sin | + | \sin(\alpha \pm \beta) &= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ |
| − | + | \cos(\alpha \pm \beta) &= \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ | |
| − | \cos | + | \tan(\alpha \pm \beta) &= \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} |
| − | + | \end{align} </math> | |
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | \end{align}</math> | ||
====Half-angle identities==== | ====Half-angle identities==== | ||
| Line 146: | Line 151: | ||
\cos \frac{A}{2} &= \pm \sqrt{\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} | \cos \frac{A}{2} &= \pm \sqrt{\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} | ||
\end{align}</math> | \end{align}</math> | ||
| + | |||
| + | ====Stereographic (or parametric) identities==== | ||
| + | |||
| + | :<math>\begin{align} | ||
| + | \sin \alpha &= \frac{2T}{1+T^2} \\ | ||
| + | \cos \alpha &= \frac{1-T^2}{1+T^2}\\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | where <math>T=\tan \frac{\alpha}{2}</math>. | ||
===Triangle identities=== | ===Triangle identities=== | ||
| − | [[Image:Triangle ABC with Sides a b c.png|thumb|240px|'''Laws of Sines and Cosines'''<math>\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}</math> | + | [[Image:Triangle ABC with Sides a b c.png|thumb|240px|'''Laws of Sines and Cosines'''<math>\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}</math> |
| + | |||
<math>\cos C=\frac{a^2+b^2-c^2}{2ab}</math>]] | <math>\cos C=\frac{a^2+b^2-c^2}{2ab}</math>]] | ||
In the following identities, ''A'', ''B'' and ''C'' are the angles of a triangle and ''a'', ''b'' and ''c'' are the lengths of sides of the triangle opposite the respective angles. | In the following identities, ''A'', ''B'' and ''C'' are the angles of a triangle and ''a'', ''b'' and ''c'' are the lengths of sides of the triangle opposite the respective angles. | ||
| Line 155: | Line 170: | ||
The '''[[law of sines]]''' (also know as the "sine rule") for an arbitrary triangle states: | The '''[[law of sines]]''' (also know as the "sine rule") for an arbitrary triangle states: | ||
| − | :<math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R</math> | + | :<math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,</math> |
where ''R'' is the radius of the [[circumcircle]] of the triangle. | where ''R'' is the radius of the [[circumcircle]] of the triangle. | ||
| Line 166: | Line 181: | ||
or equivalently: | or equivalently: | ||
| − | :<math>\cos C=\frac{a^2+b^2-c^2}{2ab}\,</math> | + | :<math>\cos C=\frac{a^2+b^2-c^2}{2ab}.\,</math> |
====Law of tangents==== | ====Law of tangents==== | ||
| Line 176: | Line 191: | ||
== See also == | == See also == | ||
* [[Uses of trigonometry]] | * [[Uses of trigonometry]] | ||
| + | * [[Trigonometric functions]] | ||
* [[List of basic trigonometry topics]] | * [[List of basic trigonometry topics]] | ||
* [[Trigonometric identity]] | * [[Trigonometric identity]] | ||
* [[Trigonometry in Galois fields]] | * [[Trigonometry in Galois fields]] | ||
| + | * [[List of triangle topics]] | ||
| + | |||
| + | ==Notes== | ||
| + | {{reflist}} | ||
==References== | ==References== | ||
| − | + | ||
| + | Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press. | ||
| + | |||
| + | Weisstein, Eric W. "Trigonometric Addition Formulas". Wolfram MathWorld. | ||
==External links== | ==External links== | ||
| Line 191: | Line 214: | ||
* [http://mathdl.maa.org/convergence/1/?pa=content&sa=viewDocument&nodeId=212&bodyId=81 Benjamin Banneker's Trigonometry Puzzle] at [http://mathdl.maa.org/convergence/1/ Convergence] | * [http://mathdl.maa.org/convergence/1/?pa=content&sa=viewDocument&nodeId=212&bodyId=81 Benjamin Banneker's Trigonometry Puzzle] at [http://mathdl.maa.org/convergence/1/ Convergence] | ||
* [http://www.math10.com/en/algebra/sin-cos-tan-cot.html Trigonometry] | * [http://www.math10.com/en/algebra/sin-cos-tan-cot.html Trigonometry] | ||
| + | * [http://www.clarku.edu/~djoyce/trig/ Dave's Short Course in Trigonometry] by David Joyce of [[Clark University]] | ||
{{Mathematics-footer}} | {{Mathematics-footer}} | ||
| − | + | [[Category:Trigonometry| ]] | |
| − | |||
| − | [[Category:Trigonometry | ||
| − | |||
<!-- interwiki —> | <!-- interwiki —> | ||
| + | |||
| + | [[af:Driehoeksmeting]] | ||
| + | [[ar:حساب مثلثات]] | ||
| + | [[az:Triqonometriya]] | ||
| + | [[bn:ত্রিকোণমিতি]] | ||
| + | [[zh-min-nan:Saⁿ-kak-hoat]] | ||
| + | [[be:Трыганаметрыя]] | ||
| + | [[be-x-old:Трыганамэтрыя]] | ||
| + | [[bs:Trigonometrija]] | ||
| + | [[bg:Тригонометрия]] | ||
| + | [[ca:Trigonometria]] | ||
| + | [[cs:Trigonometrie]] | ||
| + | [[cy:Trigonometreg]] | ||
| + | [[da:Trigonometri]] | ||
| + | [[de:Trigonometrie]] | ||
| + | [[el:Τριγωνομετρία]] | ||
| + | [[eml:Trigonometrî]] | ||
| + | [[es:Trigonometría]] | ||
| + | [[eo:Trigonometrio]] | ||
| + | [[eu:Trigonometria]] | ||
| + | [[fa:مثلثات]] | ||
| + | [[fr:Trigonométrie]] | ||
| + | [[gl:Trigonometría]] | ||
| + | [[ko:삼각법]] | ||
| + | [[hi:त्रिकोणमिति]] | ||
| + | [[hr:Trigonometrija]] | ||
| + | [[id:Trigonometri]] | ||
| + | [[it:Trigonometria]] | ||
| + | [[he:טריגונומטריה]] | ||
| + | [[ka:ტრიგონომეტრია]] | ||
| + | [[ku:Trigonometri]] | ||
| + | [[lo:ໄຕມຸມ]] | ||
| + | [[la:Trigonometria]] | ||
| + | [[lv:Trigonometrija]] | ||
| + | [[lt:Trigonometrija]] | ||
| + | [[hu:Trigonometria]] | ||
| + | [[mk:Тригонометрија]] | ||
| + | [[ml:ത്രികോണമിതി]] | ||
| + | [[mr:त्रिकोणमिती]] | ||
| + | [[ms:Trigonometri]] | ||
| + | [[nl:Goniometrie]] | ||
| + | [[ja:三角法]] | ||
| + | [[no:Trigonometri]] | ||
| + | [[nn:Trigonometri]] | ||
| + | [[uz:Trigonometriya]] | ||
[[pa:ਤਿਕੋਣਮਿਤੀ]] | [[pa:ਤਿਕੋਣਮਿਤੀ]] | ||
| + | [[pl:Trygonometria]] | ||
| + | [[pt:Trigonometria]] | ||
| + | [[ro:Trigonometrie]] | ||
| + | [[qu:Wamp'artupuykama]] | ||
| + | [[ru:Тригонометрия]] | ||
| + | [[scn:Trigunomitrìa]] | ||
| + | [[simple:Trigonometry]] | ||
| + | [[sk:Trigonometria]] | ||
| + | [[sl:Trigonometrija]] | ||
| + | [[sr:Тригонометрија]] | ||
[[sh:Trigonometrija]] | [[sh:Trigonometrija]] | ||
| − | [[te:త్రికోణమితి ]] | + | [[fi:Trigonometria]] |
| − | + | [[sv:Trigonometri]] | |
| + | [[ta:முக்கோணவியல்]] | ||
| + | [[te:త్రికోణమితి]] | ||
| + | [[th:ตรีโกณมิติ]] | ||
| + | [[vi:Lượng giác]] | ||
| + | [[tr:Trigonometri]] | ||
| + | [[uk:Тригонометрія]] | ||
| + | [[zh-yue:三角學]] | ||
| + | [[bat-smg:Trėguonuometrėjė]] | ||
| + | [[zh:三角学]] | ||
Revision as of 14:53, 3 September 2008
Template:Pp-move-vandalism
Trigonometry (from Greek Τριγωνομετρία "tri = three" + "gon = angle" + "metr[y] = to measure") is a branch of mathematics that deals with triangles, particularly those plane triangles in which one angle has 90 degrees (right triangles). Trigonometry deals with relationships between the sides and the angles of triangles and with the trigonometric functions, which describe those relationships.
Trigonometry has applications in both pure mathematics and in applied mathematics, where it is essential in many branches of science and technology. It is usually taught in secondary schools either as a separate course or as part of a precalculus course. Trigonometry is informally called "trig" or "trigo".
A branch of trigonometry, called spherical trigonometry, studies triangles on spheres, and is important in astronomy and navigation.
History
Trigonometry was developed for use in sailing as a navigation method used with astronomy.[1] The origins of trigonometry can be traced to the civilizations of ancient Egypt, Mesopotamia and the Indus Valley (India), more than 4000 years ago.[citation needed] The common practice of measuring angles in degrees, minutes and seconds comes from the Babylonian's base sixty system of numeration.
The first recorded use of trigonometry came from the Hellenistic mathematician Hipparchus[1] circa 150 B.C.E., who compiled a trigonometric table using the sine for solving triangles. Ptolemy further developed trigonometric calculations circa 100 C.E.
The ancient Sinhalese in Sri Lanka, when constructing reservoirs in the Anuradhapura kingdom, used trigonometry to calculate the gradient of the water flow. Archeological research also provides evidence of trigonometry used in other unique hydrological structures dating back to 4 B.C.E.[citation needed]
The Indian mathematician Aryabhata in 499, gave tables of half chords which are now known as sine tables, along with cosine tables. He used zya for sine, kotizya for cosine, and otkram zya for inverse sine, and also introduced the versine. Another Indian mathematician, Brahmagupta in 628, used an interpolation formula to compute values of sines, up to the second order of the Newton-Stirling interpolation formula.
In the 10th century, the Persian mathematician and astronomer Abul Wáfa introduced the tangent function and improved methods of calculating trigonometry tables. He established the angle addition identities, e.g. sin (a + b), and discovered the sine formula for spherical geometry:
Also in the late 10th and early 11th centuries, the Egyptian astronomer Ibn Yunus performed many careful trigonometric calculations and demonstrated the formula
- .
Persian mathematician Omar Khayyám (1048-1131) combined trigonometry and approximation theory to provide methods of solving algebraic equations by geometrical means. Khayyam solved the cubic equation and found a positive root of this cubic by considering the intersection of a rectangular hyperbola and a circle. An approximate numerical solution was then found by interpolation in trigonometric tables.
Detailed methods for constructing a table of sines for any angle were given by the Indian mathematician Bhaskara in 1150, along with some sine and cosine formulae. Bhaskara also developed spherical trigonometry.
The 13th century Persian mathematician Nasir al-Din Tusi, along with Bhaskara, was probably the first to treat trigonometry as a distinct mathematical discipline. Nasir al-Din Tusi in his Treatise on the Quadrilateral was the first to list the six distinct cases of a right angled triangle in spherical trigonometry.
In the 14th century, Persian mathematician al-Kashi and Timurid mathematician Ulugh Beg (grandson of Timur) produced tables of trigonometric functions as part of their studies of astronomy.
The mathematician Bartholemaeus Pitiscus published an influential work on trigonometry in 1595 which may have coined the word "trigonometry" itself.
Overview
If one angle of a triangle is 90 degrees and one of the other angles is known, the third is thereby fixed, because the three angles of any triangle add up to 180 degrees. The two acute angles therefore add up to 90 degrees: they are complementary angles. The shape of a right triangle is completely determined, up to similarity, by the angles. This means that once one of the other angles is known, the ratios of the various sides are always the same regardless of the overall size of the triangle. These ratios are given by the following trigonometric functions of the known angle A, where a, b and c refer to the lengths of the sides in the accompanying figure:
- The sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
- The cosine function (cos), defined as the ratio of the adjacent leg to the hypotenuse.
- The tangent function (tan), defined as the ratio of the opposite leg to the adjacent leg.
The hypotenuse is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle, and one of the two sides adjacent to angle A. The adjacent leg is the other side that is adjacent to angle A. The opposite side is the side that is opposite to angle A. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. Many people find it easy to remember what sides of the right triangle are equal to sine, cosine, or tangent, by memorizing the word SOH-CAH-TOA (see below under Mnemonics).
The reciprocals of these functions are named the cosecant (csc or cosec), secant (sec) and cotangent (cot), respectively. The inverse functions are called the arcsine, arccosine, and arctangent, respectively. There are arithmetic relations between these functions, which are known as trigonometric identities.
With these functions one can answer virtually all questions about arbitrary triangles by using the law of sines and the law of cosines. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and an angle or two angles and a side or three sides are known. These laws are useful in all branches of geometry, since every polygon may be described as a finite combination of triangles.
Extending the definitions
The above definitions apply to angles between 0 and 90 degrees (0 and π/2 radians) only. Using the unit circle, one can extend them to all positive and negative arguments (see trigonometric function). The trigonometric functions are periodic, with a period of 360 degrees or 2π radians. That means their values repeat at those intervals.
The trigonometric functions can be defined in other ways besides the geometrical definitions above, using tools from calculus and infinite series. With these definitions the trigonometric functions can be defined for complex numbers. The complex function cis is particularly useful
See Euler's and De Moivre's formulas.
Mnemonics
Students often use mnemonics to remember facts and relationships in trigonometry. For example, the sine, cosine, and tangent ratios in a right triangle can be remembered by representing them as strings of letters, as in SOH-CAH-TOA.
- Sine = Opposite ÷ Hypotenuse
- Cosine = Adjacent ÷ Hypotenuse
- Tangent = Opposite ÷ Adjacent
Alternatively, one can devise sentences which consist of words beginning with the letters to be remembered. For example, to recall that Tan = Opposite/Adjacent, the letters T-O-A must be remembered. Any memorable phrase constructed of words beginning with the letters T-O-A will serve.
It is of ethnographic interest to note that the mnemonic TOA-CAH-SOH can be translated in the local Singaporean Hokkien dialect to 'big-legged woman', serving as an additional learning aid for students in Singapore[2].
Another type of mnemonic describes facts in a simple, memorable way, such as "Plus to the right, minus to the left; positive height, negative depth," which refers to trigonometric functions generated by a revolving line.
Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy. Slide rules had special scales for trigonometric functions.
Today scientific calculators have buttons for calculating the main trigonometric functions (sin, cos, tan and sometimes cis) and their inverses. Most allow a choice of angle measurement methods, degrees, radians and, sometimes, Grad. Most computer programming languages provide function libraries that include the trigonometric functions. The floating point unit hardware incorporated into the microprocessor chips used in most personal computers have built in instructions for calculating trigonometric functions.
Applications of trigonometry
There are an enormous number of applications of trigonometry and trigonometric functions. For instance, the technique of triangulation is used in astronomy to measure the distance to nearby stars, in geography to measure distances between landmarks, and in satellite navigation systems. The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.
Fields which make use of trigonometry or trigonometric functions include astronomy (especially, for locating the apparent positions of celestial objects, in which spherical trigonometry is essential) and hence navigation (on the oceans, in aircraft, and in space), music theory, acoustics, optics, analysis of financial markets, electronics, probability theory, statistics, biology, medical imaging (CAT scans and ultrasound), pharmacy, chemistry, number theory (and hence cryptology), seismology, meteorology, oceanography, many physical sciences, land surveying and geodesy, architecture, phonetics, economics, electrical engineering, mechanical engineering, civil engineering, computer graphics, cartography, crystallography and game development.
Common formulae
Certain equations involving trigonometric functions are true for all angles and are known as trigonometric identities. Many express important geometric relationships. For example, the Pythagorean identities are an expression of the Pythagorean Theorem. Here are some of the more commonly used identities, as well as the most important formulae connecting angles and sides of an arbitrary triangle. For more identities see trigonometric identity.
Trigonometric identities
| Trigonometry |
|
History |
| Reference |
|
List of identities |
| Euclidean theory |
|
Law of sines |
| Calculus |
|
The Trigonometric integral |
Pythagorean identities
Sum and product identities
Sum to product:
Product to sum[3]:
Sine, cosine, and tangent of a sum
Detailed, diagramed proofs of the first two of these formulas
are available
for download as a four-page PDF document
at File:Sine Cos Proofs.pdf.
Half-angle identities
Note that is correct, it means it may be either one, depending on the value of A/2.
Stereographic (or parametric) identities
where .
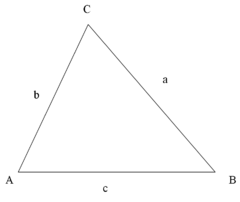
Triangle identities
In the following identities, A, B and C are the angles of a triangle and a, b and c are the lengths of sides of the triangle opposite the respective angles.
Law of sines
The law of sines (also know as the "sine rule") for an arbitrary triangle states:
where R is the radius of the circumcircle of the triangle.
Law of cosines
The law of cosines (also known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
or equivalently:
Law of tangents
The law of tangents:
See also
- Uses of trigonometry
- Trigonometric functions
- List of basic trigonometry topics
- Trigonometric identity
- Trigonometry in Galois fields
- List of triangle topics
Notes
- ↑ Christopher M. Linton (2004). From Eudoxus to Einstein: A History of porn. Cambridge University Press.
- ↑ Trigonometry - My Grandmother Also Can Do This!. Retrieved 2008-08-30. Diary of a Private O Level Maths Tutor in Singapore
- ↑ Weisstein, Eric W. Trigonometric Addition Formulas. Wolfram MathWorld.
ReferencesISBN links support NWE through referral fees
Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy . Cambridge University Press.
Weisstein, Eric W. "Trigonometric Addition Formulas". Wolfram MathWorld.
External links
- Trigonometric Delights, by Eli Maor, Princeton University Press, 1998. Ebook version, in PDF format, full text presented.
- Trigonometry by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
- Trigonometry on PlainMath.net Trigonometry Articles from PlainMath.Net
- Trigonometry on Mathwords.com index of trigonometry entries on Mathwords.com
- Benjamin Banneker's Trigonometry Puzzle at Convergence
- Trigonometry
- Dave's Short Course in Trigonometry by David Joyce of Clark University
| Major fields of Mathematics | Edit |
|---|---|
| Logic | Set theory | Combinatorics | Probability | Mathematical statistics | Number theory | Optimization | Linear algebra | Abstract algebra | Category theory | Algebraic geometry | Geometry | Topology | Algebraic topology | Analysis | Differential equations | Functional analysis | Numerical analysis | |
af:Driehoeksmeting
ar:حساب مثلثات
az:Triqonometriya
bn:ত্রিকোণমিতি
zh-min-nan:Saⁿ-kak-hoat
be:Трыганаметрыя
be-x-old:Трыганамэтрыя
bs:Trigonometrija
bg:Тригонометрия
ca:Trigonometria
cs:Trigonometrie
cy:Trigonometreg
da:Trigonometri
de:Trigonometrie
el:Τριγωνομετρία
eml:Trigonometrî
es:Trigonometría
eo:Trigonometrio
eu:Trigonometria
fa:مثلثات
fr:Trigonométrie
gl:Trigonometría
ko:삼각법
hi:त्रिकोणमिति
hr:Trigonometrija
id:Trigonometri
it:Trigonometria
he:טריגונומטריה
ka:ტრიგონომეტრია
ku:Trigonometri
lo:ໄຕມຸມ
la:Trigonometria
lv:Trigonometrija
lt:Trigonometrija
hu:Trigonometria
mk:Тригонометрија
ml:ത്രികോണമിതി
mr:त्रिकोणमिती
ms:Trigonometri
nl:Goniometrie
ja:三角法
no:Trigonometri
nn:Trigonometri
uz:Trigonometriya
pa:ਤਿਕੋਣਮਿਤੀ
pl:Trygonometria
pt:Trigonometria
ro:Trigonometrie
qu:Wamp'artupuykama
ru:Тригонометрия
scn:Trigunomitrìa
simple:Trigonometry
sk:Trigonometria
sl:Trigonometrija
sr:Тригонометрија
sh:Trigonometrija
fi:Trigonometria
sv:Trigonometri
ta:முக்கோணவியல்
te:త్రికోణమితి
th:ตรีโกณมิติ
vi:Lượng giác
tr:Trigonometri
uk:Тригонометрія
zh-yue:三角學
bat-smg:Trėguonuometrėjė
zh:三角学








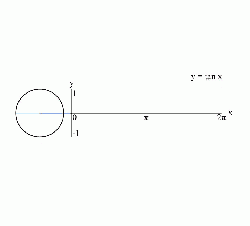
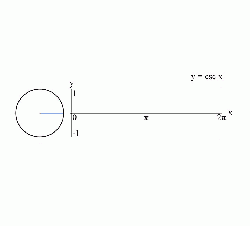




![{\displaystyle {\begin{aligned}\cos \alpha \,\cos \beta &={\frac {1}{2}}[\cos(\alpha -\beta )+\cos(\alpha +\beta )]\\\sin \alpha \,\sin \beta &={\frac {1}{2}}[\cos(\alpha -\beta )-\cos(\alpha +\beta )]\\\cos \alpha \,\sin \beta &={\frac {1}{2}}[\sin(\alpha +\beta )-\sin(\alpha -\beta )]\\\sin \alpha \,\cos \beta &={\frac {1}{2}}[\sin(\alpha +\beta )+\sin(\alpha -\beta )]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96eaeb9f421aaa76e91733c7ff755243b6131df)










![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan \left[{\tfrac {1}{2}}(A+B)\right]}{\tan \left[{\tfrac {1}{2}}(A-B)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21e586b944db5905c0bc192c18573ecb20e63503)