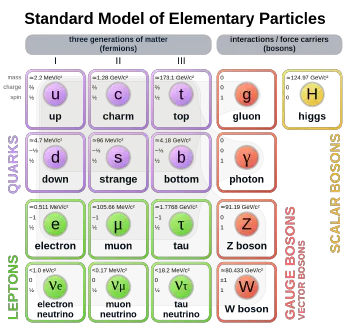
In particle physics, fermions are a group of elementary (or fundamental) particles that are the building blocks of matter. In the Standard Model, elementary particles are classified as fermions and bosons. Fermions are usually related with matter, whereas bosons are related with fundamental forces (or radiation).
Fermions are subdivided into quarks and leptons. Quarks are fermions that couple with a class of bosons known as gluons to form composite particles such as protons and neutrons. Leptons are those fermions that do not undergo coupling with gluons. Electrons are a well-known example of leptons.
Fermions come in pairs, and in three "generations." Everyday matter is composed of the first generation of fermions: two leptons, the electron and electron-neutrino; and two quarks, called Up and Down. Fermions obey what is known as "Fermi-Dirac statistics" and are named after Enrico Fermi.
Basic properties
In theoretical terms, one major difference between fermions and bosons is related to a property known as "spin."[1] Fermions have odd half-integer spin (1/2, 3/2, 5/2, and so forth), whereas bosons have integer spin (0, 1, 2, and so forth).[2] (Here, "spin" refers to the angular momentum quantum number.) Fermions obey Fermi-Dirac statistics, which means that when one swaps two fermions, the wavefunction of the system changes sign.
Given that each fermion has half-integer spin, when an observer circles a fermion (or when the fermion rotates 360° about its axis), the wavefunction of the fermion changes sign. A related phenomenon is called an antisymmetric wavefunction behavior of a fermion.
As particles with half-integer spin, fermions obey the Pauli exclusion principle: no two fermions can exist in the same quantum state at the same time. Thus, for more than one fermion to occupy the same place in space, certain properties (such as spin) of each fermion in the group must be different from the rest. The operation of the Pauli exclusion principle is used to explain the "rigidness" or "stiffness" of ordinary matter (contributing to the Young modulus of matter), and the stability of the electron shells of atoms (thus the stability of atomic matter). This principle is also responsible for the complexity of atoms (making it impossible for all atomic electrons to occupy the same energy level), thus making complex chemistry possible. In addition, this principle is said to be responsible for the pressure within degenerate matter, which largely governs the equilibrium state of white dwarfs and neutron stars.
In large systems, the difference between bosonic and fermionic statistics is apparent only at high densities, when their wave functions overlap. At low densities, both types of statistics are well approximated by Maxwell-Boltzmann statistics, which is described by classical mechanics.
Elementary fermions
As noted above, elementary particles are classified as fermions and bosons, and elementary fermions are subdivided into quarks and leptons. When quarks are coupled together, they form composite fermions such as protons and neutrons. Leptons include the electron and similar, heavier particles (muon and tau) and neutrinos.
The known fermions of left-handed helicity interact through the weak interaction, but the known right-handed fermions do not. Or, put another way, only left-handed fermions and right-handed anti-fermions couple to the W boson.
Flavors of fermions
There are 24 fundamental (or elementary) types of fermions, referred to as fermionic "flavors." They consist of 12 quarks and 12 leptons, as listed below.
- 12 leptons - six particles and six corresponding antiparticles
Composite fermions
In addition to elementary fermions and bosons, nonrelativistic composite particles made up of more fundamental particles bound together through a potential energy are composite fermions or bosons, depending only on the number of elementary fermions they contain:
- A composite particle containing an even number of elementary fermions is a boson. Examples:
- A composite particle containing an odd number of elementary fermions is a fermion. Examples:
The number of bosons within a composite particle made up of simple particles bound with a potential has no effect on whether the composite particle is a boson or a fermion.
In a quantum field theory, the situation is more interesting. There can be field configurations of bosons that are topologically twisted. These are coherent states that behave like particles, and they can be fermionic even if all the elementary particles are bosons. This situation was discovered by Tony Skyrme in the early 1960s, so fermions made of bosons are named Skyrmions.
Fermionic or bosonic behavior of a composite particle (or system) is seen only at large distances (compared to the size of the system). At proximity, where spatial structure begins to be important, a composite particle (or system) behaves according to its constituent makeup. For example, two atoms of helium cannot share the same space if it is comparable by size to the size of the inner structure of the helium atom itself (~10−10 m)—despite bosonic properties of the helium atoms. Thus, liquid helium has finite density comparable to the density of ordinary liquid matter.
Table of fermions and their properties
The following table is based in part on data gathered by the Particle Data Group.[3]
| Generation 1 | |||||||
|---|---|---|---|---|---|---|---|
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Electron | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle e^{-}\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 511 keV | ||||
| Positron | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 511 keV | ||||
| Electron-neutrino | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +1/2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | < 2 eV **** | ||||
| Up quark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2/3\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +1/2\,} | ~ 3 MeV *** | ||||
| Up antiquark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\bar {u}}\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -4/3\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {\bar {3}}}\,} | ~ 3 MeV *** | |||
| Down quark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle d\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -1/3\,} | ~ 6 MeV *** | ||||
| Down antiquark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\bar {d}}\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2/3\,} | ~ 6 MeV *** | ||||
| Generation 2 | |||||||
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Muon | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 106 MeV | |||||
| Antimuon | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 106 MeV | ||||
| Muon-neutrino | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +1/2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | < 2 eV **** | ||||
| Charm quark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2/3\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +1/2\,} | ~ 1.337 GeV | ||||
| Charm antiquark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -4/3\,} | ~ 1.3 GeV | |||||
| Strange quark | ~ 100 MeV | ||||||
| Strange antiquark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2/3\,} | ~ 100 MeV | |||||
| Generation 3 | |||||||
| Fermion (left-handed) |
Symbol | Electric charge |
Weak isospin |
Weak hypercharge |
Color charge * |
Mass ** | |
| Tau lepton | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 1.78 GeV | |||||
| Anti-tau lepton | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | 1.78 GeV | ||||
| Tau-neutrino | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +1/2\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\mathbf {1}}\,} | < 2 eV **** | ||||
| Top quark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle +2/3\,} | 171 GeV | |||||
| Top antiquark | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\bar {t}}\,} | Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -4/3\,} | 171 GeV | ||||
| Bottom quark | ~ 4.2 GeV | ||||||
| Bottom antiquark | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{b}\,} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1/3\,} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\,} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +2/3\,} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{\bar{3}}\,} | ~ 4.2 GeV | |
Notes:
| |||||||
Notes
- ↑ The spin-statistics theorem identifies the resulting quantum statistics that differentiates fermions from bosons.
- ↑ Martinus Veltman, Facts and Mysteries in Elementary Particle Physics (River Edge, NJ: World Scientific, 2003, ISBN 981238149X).
- ↑ W.-M. Yao et al. (Particle Data Group) (2006), Quarks J. Phys. G 33:1. Retrieved September28. 2022.
- ↑ B. Kayser (Fermilab) (Sep. 2005), Neutrino mass, mixing, and flavor change Particle Data Group. Retrieved September 28, 2022.
ReferencesISBN links support NWE through referral fees
- Cottingham, W.N., and D.A. Greenwood. An Introduction to the Standard Model of Particle Physics, 2nd ed. Cambridge, UK: Cambridge University Press, 2007. ISBN 978-0521852494
- Griffiths, David J. Introduction to Elementary Particles. New York: Wiley, 1987. ISBN 0471603864
- Halzen, Francis, and Alan D. Martin. Quarks and Leptons: An Introductory Course in Modern Particle Physics. New York: Wiley, 1991 (original 1984). ISBN 0471887412
- Martin, B.R. Nuclear and Particle Physics: An Introduction. Chichester: John Wiley, 2006. ISBN 978-0470025321
- Povh, Bogdan. Particles and Nuclei: An Introduction to the Physical Concepts. Berlin: Springer-Verlag, 1995. ISBN 0387594396
- Veltman, Martinus. Facts and Mysteries in Elementary Particle Physics. River Edge, NJ: World Scientific, 2003. ISBN 981238149X
External links
All links retrieved March 26, 2024.
- Spin Classification, Fermions, Bosons, Bose-Einstein Condensation
- When bosons behave like fermions Physics World
- Review of Particle Physics Particle Data Group.
- Physics: Fermion Definition ThoughtCo
| Particles in physics | |
|---|---|
| elementary particles | Elementary fermions: Quarks: u · d · s · c · b · t • Leptons: e · μ · τ · νe · νμ · ντ Elementary bosons: Gauge bosons: γ · g · W± · Z0 • Ghosts |
| Composite particles | Hadrons: Baryons(list)/Hyperons/Nucleons: p · n · Δ · Λ · Σ · Ξ · Ω · Ξb • Mesons(list)/Quarkonia: π · K · ρ · J/ψ · Υ Other: Atomic nucleus • Atoms • Molecules • Positronium |
| Hypothetical elementary particles | Superpartners: Axino · Dilatino · Chargino · Gluino · Gravitino · Higgsino · Neutralino · Sfermion · Slepton · Squark Other: Axion · Dilaton · Goldstone boson · Graviton · Higgs boson · Tachyon · X · Y · W' · Z' |
| Hypothetical composite particles | Exotic hadrons: Exotic baryons: Pentaquark • Exotic mesons: Glueball · Tetraquark Other: Mesonic molecule |
| Quasiparticles | Davydov soliton · Exciton · Magnon · Phonon · Plasmon · Polariton · Polaron |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.