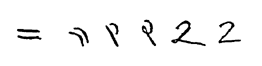2 (number)
2
| |
|
List of numbers — Integers | |
| Cardinal | 2 two |
| Ordinal number | 2nd second |
| Numeral system | binary |
| Factorization | prime |
| Gaussian integer factorization | |
| Divisors | 1, 2 |
| Greek numeral | β' |
| Roman numeral | II |
| Roman numeral (Unicode) | Ⅱ, ⅱ |
| Arabic | ٢ |
| Ge'ez | ፪ |
| Bengali | ২ |
| Chinese numeral | 二,弍,贰,貳 |
| Devanāgarī | २ |
| Hebrew | ב (Bet) |
| Khmer | ២ |
| Korean | 이 |
| Thai | ๒ |
| prefixes | di- (from Greek)
duo- bi- (from Latin) twi- (Old English) |
| Binary | 10 |
| Octal | 2 |
| Duodecimal | 2 |
| Hexadecimal | 2 |
2 (two) is a number, numeral, and glyph that represents the number. It is the natural number[1] that follows 1 and precedes 3. It is an integer and a cardinal number, that is, a number that is used for counting.[2] In addition, it is classified as a real number,[3] distinguishing it from imaginary numbers.
The number two also represents a pair or duality. In biology, sexual reproduction requires the mating of two organisms, male and female, or the uniting of materials provided by male and female organisms. Eastern philosophy points to such dual characteristics as masculinity and femininity (in the animate world), or positivity and negativity (in the inanimate world), and categorizes them as Yang and Yin (in Chinese). Although some consider good and evil as an example of Yang-Yin characteristics, there is a fundamental difference: evil (such as hatred and violence) flourishes by destroying goodness (such as love and kindness), whereas male and female flourish and multiply their kind by uniting in harmony and love.
Evolution of the glyph
The glyph currently used in the Western world to represent the number 2 traces its roots back to the Brahmin Indians, who wrote 2 as two horizontal lines. (It is still written that way in modern Chinese and Japanese.) The Gupta script rotated the two lines 45 degrees, making them diagonal, and sometimes also made the top line shorter and made its bottom end curve towards the center of the bottom line. Apparently for speed, the Nagari started making the top line more like a curve and connecting to the bottom line. The Ghubar Arabs made the bottom line completely vertical, and now the glyph looked like a dotless closing question mark. Restoring the bottom line to its original horizontal position, but keeping the top line as a curve that connects to the bottom line leads to our modern glyph.[4]
In fonts with text figures, 2 usually has the same height as a lowercase X, for example, ![]() .
.
In mathematics
Two has many properties in mathematics.[5] An integer is called even if it is divisible by 2. For integers written in a numeral system based on an even number, such as decimal and hexadecimal, divisibility by 2 is easily tested by merely looking at the one's place digit. If it is even, then the whole number is even. In particular, when written in the decimal system, all multiples of 2 will end in 0, 2, 4, 6, or 8.
Two is the smallest and first prime number, and the only even one. (For this reason, it is sometimes humorously called "the oddest prime".) The next prime number is three. Two and three are the only two consecutive prime numbers. 2 is the first Sophie Germain prime, the first factorial prime, the first Lucas prime, and the first Smarandache-Wellin prime. It is an Eisenstein prime with no imaginary part and real part of the form . It is also a Stern prime, a Pell number, and a Markov number, appearing in infinitely many solutions to the Markov Diophantine equation involving odd-indexed Pell numbers.
It is the third Fibonacci number, and the third and fifth Perrin numbers.
Despite being a prime, two is also a highly composite number, because it has more divisors than the number one. The next highly composite number is four.
Vulgar fractions with 2 or 5 in the denominator do not yield infinite decimal expansions, as is the case with most primes, because 2 and 5 are factors of ten, the decimal base.
Two is the base of the simplest numeral system in which natural numbers can be written concisely, being the length of the number a logarithm of the value of the number (whereas in base 1 the length of the number is the value of the number itself); the binary system is used in computers.
For any number x:
- x+x = 2•x addition to multiplication
- x•x = x2 multiplication to exponentiation
- xx = x↑↑2 exponentiation to tetration
Two also has the unique property that 2+2 = 2•2 = 2²=2↑↑2=2↑↑↑2, and so on, no matter how high the operation is.
Two is the only number x such that the sum of the reciprocals of the powers of x equals itself. In symbols:
This comes from the fact that:
Powers of two are central to the concept of Mersenne primes, and important to computer science. Two is the first Mersenne prime exponent.
Taking the square root of a number is such a common mathematical operation, that the spot on the root sign where the exponent would normally be written for cubic roots and other such roots, is left blank for square roots, as it is considered tacit.
The square root of two was the first known irrational number.
The smallest field has two elements.
In the set-theoretical construction of the natural numbers, 2 is identified with the set . This latter set is important in category theory: it is a subobject classifier in the category of sets.
Two is a primorial, as well as its own factorial. Two often occurs in numerical sequences, such as the Fibonacci number sequence, but not quite as often as one does. Two is also a Motzkin number, a Bell number, an all-Harshad number, a meandric number, a semi-meandric number, and an open meandric number.
Two is the number of n-Queens Problem solutions for n = 4. With one exception, all known solutions to Znám's problem start with 2.
Two also has the unique property such that:
and also
for a not equal to zero
Two has a connection to triangular numbers:
Where gives the nth d-dimensional simplex number. When d=2,
The number of domino tilings of a 2×2 checkerboard is 2.
List of basic calculations
- Multiplication
| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| Multiplication | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| Multiplication | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 | |
|---|---|---|---|---|---|---|---|---|---|
| 42 | 44 | 46 | 48 | 50 | 100 | 200 | 2000 |
- Division
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.5 | 0.4 | 0.25 | 0.2 | |||||
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| Division | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| 5.5 | 6 | 6.5 | 7 | 7.5 |
- Exponentiation
| Exponentiation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | |
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Exponentiation | 11 | 12 | 13 |
|---|---|---|---|
| 2048 | 4096 | 8192 | |
| 121 | 144 | 169 |
In science
Chemistry
In chemistry, 2 is the atomic number of helium. Group 2 in the periodic table of elements consists of the alkaline earth metals, which commonly have a valence of +2. Also, period 2 in the periodic table consists of the eight elements lithium through neon.
Biology
In the structures of many living organisms (especially mammals), various features occur in pairs. Examples include: eyes, ears, nostrils, jaws, forelegs (or arms), hind legs, lungs, kidneys, and so forth.
Sexual reproduction requires the mating of two organisms, male and female, or the uniting of materials provided by male and female organisms.
Studies in molecular biology have shown that each molecule of DNA usually consists of two polynucleotide strands that form a double helix.
Physics
There are two opposite and complementary electrical charges: positive and negative. Both are needed and work together in the formation of atoms and molecules.
There are two opposite and complementary magnetic poles: north and south. Both play a part in setting up a magnetic field.
In the electronic configuration of an atom, a maximum of two electrons (of opposite spin) may occupy a given orbital at any instant.
In nuclear physics, 2 is the first magic number. A magic number (in this case) is the number of nucleons (protons and neutrons) in the atomic nucleus, such that they are arranged into complete shells in the nucleus.[6]
Astronomy
- A binary star is a stellar system consisting of two stars orbiting around their center of mass.
- The Roman numeral II is usually applied to the second-discovered satellite of a planet or minor planet (such as Pluto II or (87) Sylvia II Remus).
- The Roman numeral II also stands for bright giant in the Yerkes spectral classification scheme.
- Two is the Saros number of the solar eclipse series that began on May 4, 2861 B.C.E. and ended on June 21, 1563 B.C.E. The duration of Saros series 2 was 1298.17 years, and it contained 73 solar eclipses.[7]
- Two is the Saros number of the lunar eclipse series that began on March 3, 2523 B.C.E. and ended on April 22, 1225 B.C.E. The duration of Saros series 2 was 1298.17 years, and it contained 73 lunar eclipses.[8]
Recycling
- 2 is the resin identification code used in recycling to identify high-density polyethylene.
In religion, philosophy, and culture
Eastern philosophy
In Eastern philosophy, a well-known dualism is that of Yang and Yin (in Chinese), or Yang and Eum (in Korean). They stand for pairs of characteristics such as masculinity and femininity, or positivity and negativity. Some consider good and evil as an example of Yang-Yin characteristics, but there is a fundamental difference: evil (such as hatred and violence) flourishes by destroying goodness (such as love and kindness), whereas male and female flourish by uniting in harmony.
Marxism versus religious teachings
In Marxist ideology, a pair known as "thesis" and "antithesis" have to clash with each other for progress to occur. This philosophy, however, became a justification for class warfare, in which the "lower class" were encouraged to destroy the "upper class." By contrast, various major religions place value on all people, regardless of class, encouraging harmony among people guided by God's love.
Judaism
- The Book of Genesis notes that the first humans were a couple, Adam and Eve. One may recognize this as being necessary for reproduction and multiplication of the human race.
- In the story about Noah, the animals boarded Noah's Ark two by two. One may infer that they were male and female pairs, to allow those species to survive through sexual reproduction.
- The Ten Commandments were given in the form of two tablets (Shnei Luchot HaBrit).
- Two candles are traditionally kindled to usher in the Shabbat, recalling the two different ways Shabbat is referred to in the two times the Ten Commandments are recorded in the Torah. These two expressions are known in Hebrew as שמור וזכור ("guard" and "remember"), as in "Guard the Shabbat day to sanctify it" (Deut. 5:12) and "Remember the Shabbat day to sanctify it" (Ex. 20:8).
- Two challahs (lechem mishnah) are placed on the table for each Shabbat meal and a blessing made over them, to commemorate the double portion of manna that fell in the desert every Friday to cover that day's meals and the Shabbat meals.
- In Jewish law, the testimonies of two witnesses are required to verify and validate events, such as marriage, divorce, and a crime that warrants capital punishment.
- Rosh Hashana, the first day of the Jewish year, is a 2-day holiday
- "Second-Day Yom Tov" (Yom Tov Sheini Shebegaliyot) is a rabbinical enactment that mandates a two-day celebration for each of the one-day Jewish festivals (i.e., the first and seventh day of Passover, the day of Shavuot, the first day of Sukkot, and the day of Shemini Atzeret) outside the land of Israel.
Chinese culture
Two (二, èr) is a good number in Chinese culture. There is a Chinese saying "good things come in pairs." It is common to use double symbols in product brand names, such as double happiness, double coin, double elephants, and so forth. Cantonese people like the number two because it sounds the same as the word "easy" (易) in Cantonese.
See also
Notes
- ↑ A natural number is any number that is a positive integer, such as 1, 2, 3, 4, and so forth. Often, the number 0 is also called a natural number.
- ↑ A cardinal number indicates the quantity of things, but not the order in which they occur. By contrast, ordinal numbers are first, second, third, and so on, indicating their positions in a series.
- ↑ A real number is a number that can be given by a finite or infinite decimal representation. The term "real number" was coined to distinguish it from an "imaginary number." The set of real numbers includes rational and irrational numbers, which can be positive, negative, or zero.
- ↑ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer, (New York: Wiley, 2000, ISBN 0471393401), 393, Fig. 24.62.
- ↑ D. Wells, The Penguin Dictionary of Curious and Interesting Numbers (London: Penguin Group, 1998, ISBN 0140261494), 41–44.
- ↑ Xavier Borg, Magic numbers derived from a variable phase nuclear model The General Science Journal, January 2, 2006. Retrieved October 7, 2022.
- ↑ Saros Series 2 Saros Series Catalog of Solar Eclipses NASA Eclipse website. Retrieved October 7, 2022.
- ↑ Saros Series 2 Catalog of Lunar Eclipse Saros Series, NASA Eclipse website. Retrieved October 7, 2022.
ReferencesISBN links support NWE through referral fees
- Flegg, Graham. Numbers: Their History and Meaning. Mineola, NY: Dover Publications, 2002. ISBN 0486421651
- Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer. Translated by David Bellos et al. New York: Wiley, 2000. ISBN 0471393401
- McLeish, John. The Story of Numbers: How Mathematics Has Shaped Civilization. New York: Fawcett Columbine, 1994. ISBN 0449909387
- Menninger, Karl. Number Words and Number Symbols: A Cultural History of Numbers. New York: Dover Publications, 1992. ISBN 0486270963
- Wells, D.G. The Penguin Dictionary of Curious and Interesting Numbers. Rev. ed. London, UK: Penguin Books, 1998. ISBN 0140261494
External links
All links retrieved June 13, 2023.
- Number "2" and the human body teachers.net.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.