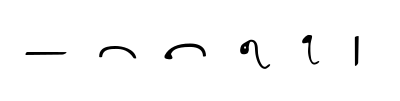1 (number)
- "One" redirects here.
1
| |
|
List of numbers — Integers | |
| Cardinal | 1 one |
| Ordinal | 1st first |
| Numeral system | unary |
| Factorization | |
| Divisors | 1 |
| Greek numeral | α' |
| Roman numeral | I |
| Roman numeral (Unicode) | Ⅰ, ⅰ |
| Arabic | ١ |
| Ge'ez | ፩ |
| Bengali | ১ |
| Chinese numeral | 一,弌,壹 |
| Korean | 일, 하나 |
| Devanāgarī | १ |
| Hebrew | א (Alef) |
| Khmer | ១ |
| Thai | ๑ |
| prefixes | mono- /haplo- (from Greek)
uni- (from Latin) |
| Binary | 1 |
| Octal | 1 |
| Duodecimal | 1 |
| Hexadecimal | 1 |
1 (one) is a number, numeral, and the glyph that represents the number. It represents a single entity and is commonly regarded as the fundamental unit of counting and measurement. For example, a line segment of "unit length" is a line segment of length 1.
In mathematics, the number 1 is the natural number[1] that follows 0 and precedes 2. It is an integer and a cardinal number, that is, a number that is used for counting.[2] In addition, it is classified as a real number,[3] distinguishing it from imaginary numbers. The number 1 is also known as the "identity element" of multiplication (or multiplicative identity)—any number multiplied by one is itself.
The number one also represents oneness or unity. For example, although science is divided into many areas of specialization, scientists recognize the unity of the natural world and the underlying unity of the sciences. In the religious world, most of today's major religions teach of a single, common God, and the importance of unity among people based on our common humanity. Culturally, people generally recognize that strength derives from unity and weakness is a product of disunity. Also, the number one is a coveted number in practically every competition, as the champion is ranked as "Number One."
Evolution of the glyph
The glyph used today in the Western world to represent the number 1, a vertical line, often with a serif at the top and sometimes a short horizontal line at the bottom, traces its roots back to the Indians, who wrote 1 as a horizontal line, as is still the case in Chinese script. The Gupta wrote it as a curved line, and the Nagari sometimes added a small circle on the left (rotated a quarter turn to the right, this 9-look-alike became the present day numeral 1 in the Gujarati and Punjabi scripts). The Nepali also rotated it to the right, but kept the circle small.[4] This eventually became the top serif in the modern numeral, but the occasional short horizontal line at the bottom probably originates from similarity with the Roman numeral I. In some European countries (e.g., Germany) the little serif at the top is sometimes extended into a long upstroke, sometimes as long as the vertical line, which can lead to confusion with the glyph for seven in other countries. Where the 1 is written with a long upstroke, the number 7 has a horizontal stroke through the vertical line.
While the shape of the 1 character has an ascender in most modern typefaces, in typefaces with text figures the character usually is of x-height, as, for example, in ![]() .
.
In mathematics
For any number x:
- x•1 = 1•x = x (1 is the multiplicative identity)
- x/1 = x (see division)
- x1 = x, 1x = 1, and for nonzero x, x0 = 1 (see exponentiation)
Using ordinary addition, we have 1 + 1 = 2.
One cannot be used as the base of a positional numeral system. Sometimes, tallying is referred to as "base 1," since only one mark (the tally) is needed, but this is not a positional notation.
The logarithms base 1 is undefined, since 1x=1 and so has no unique inverse function.
In the real number system, 1 can be represented in two ways as a recurring decimal: as 1.000... and as 0.999... (q.v.).
In the Von Neumann representation of natural numbers, 1 is defined as the set {0}. This set has cardinality 1 and hereditary rank 1. Sets like this with a single element are called singletons.
In Principia Mathematica, 1 is defined as the set of all singletons.
In a multiplicative group or monoid, the identity element is sometimes denoted "1," but "e" (from the German Einheit, unity) is more traditional. However, "1" is especially common for the multiplicative identity of a ring. (Note that this multiplicative identity is also often called "unity".)
One is its own factorial, and its own square and cube (and so on, as 1 × 1 × ... × 1 = 1). One is the first figurate number of every kind, such as triangular number, pentagonal number and centered hexagonal number to name just a few.
Because of the multiplicative identity, if f(x) is a multiplicative function, then f(1) must equal 1.
It is also the first and second numbers in the Fibonacci sequence, and is the first number in many mathematical sequences. As a matter of convention, Sloane's early Handbook of Integer Sequences added an initial 1 to any sequence that didn't already have it, and considered these initial 1's in its lexicographic ordering. Sloane's later Encyclopedia of Integer Sequences and its Web counterpart, the On-Line Encyclopedia of Integer Sequences, ignore initial ones in their lexicographic ordering of sequences, because such initial ones often correspond to trivial cases.
One is the empty product.
One is the smallest positive odd integer.
One is a harmonic divisor number.
One is often the internal representation of the Boolean constant true in computer systems.
One is neither a prime number nor a composite number, but a unit, like -1 and, in the Gaussian integers, i and -i. The fundamental theorem of arithmetic guarantees unique factorization over the integers only up to units (e.g. 4 = 22 = (-1)4×123×22).
One was formerly considered prime by some mathematicians, using the definition that a prime is divisible only by one and itself. However, this complicates the fundamental theorem of arithmetic, so modern definitions exclude units. The last professional mathematician to publicly label 1 a prime number was Henri Lebesgue in 1899.
One is one of three possible values of the Möbius function: it takes the value one for square-free integers with an even number of distinct prime factors.
One is the only odd number in the range of Euler's totient function φ(x), in the cases x = 1 and x = 2.
One is the only 1-perfect number (see multiply perfect number).
By definition, 1 is the magnitude or absolute value of a unit vector and a unit matrix (more usually called an identity matrix). Note that the term unit matrix is usually used to mean something quite different.
One is the most common leading digit in many sets of data, a consequence of Benford's law.
Egyptian people used to represent all fractions in terms of sum of fractions with numerator 1 and distinct denominators. For example, . Such representations are popularly known as Egyptian Fractions or Unit Fractions.
The Generating Function which has all coefficients 1 is given by
.
This power series converges and has finite value if, and only if, .
List of basic calculations
- Multiplication
| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Multiplication | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Multiplication | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 | |
|---|---|---|---|---|---|---|---|---|---|
| 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 |
- Division
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.25 | 0.2 | 0.125 | 0.1 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Division | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 |
- Exponentiation
| Exponentiation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Exponentiation | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Interesting multiplications
If a number containing only ones (such as 1, 11, 111, and so forth) is multiplied by itself, the results are very interesting.[5]
- 1 x 1 = 1
- 11 x 11 = 121
- 111 x 111 = 12321
- 1111 x 1111 = 1234321
- 11111 x 11111 = 123454321
In science and technology
The number one signifies unity, such as the unity of the natural world, and, by extension, unity of the sciences. For instance, studies in ecology demonstrate the interdependence of living organisms with one another and with the inanimate environment, thus forming a united whole. In addition, other interdisciplinary sciences (such as earth science, geophysics, biochemistry) demonstrate the unity of the sciences. Likewise, various technologies play interactive and interdependent roles with one another and with the sciences, such as in the development of technologies for transportation, communications, agriculture, and energy generation.
Chemistry
In chemistry, 1 is the atomic number of hydrogen, the smallest chemical element. Group 1 in the periodic table of elements consists of the alkali metals, which commonly have a valence of +1. Also, period 1 in the periodic table consists of the two elements hydrogen and helium.
Recycling
The number 1 is the resin identification code used in recycling to identify polyethylene terephthalate.
In religion and culture
The major monotheistic religions teach that there is only one God. Thus, all of humanity shares a common Creator, making all people part of one human family. This perspective leads to a recognition of the principle of unity. The Book of Psalms 133:1 says, "Behold, how good and pleasant it is when brothers dwell in unity!"[6] Thus unity is seen as a valuable goal for humanity.
The need for unity is also recognized as a goal with practical value. The aphorism "United we stand, divided we fall" is often used in team competitions, and its value is demonstrated by experience. Also, in any competition, from sports to academics, the person or team who is judged to be the best is given the rank of Number One.
See also
Notes
- ↑ A natural number is any number that is a positive integer, such as 1, 2, 3, 4, and so forth. Often, the number 0 is also called a natural number.
- ↑ A cardinal number indicates the quantity of things, but not the order in which they occur. By contrast, ordinal numbers are first, second, third, and so on, indicating their positions in a series.
- ↑ A real number is a number that can be given by a finite or infinite decimal representation. The term "real number" was coined to distinguish it from an "imaginary number." The set of real numbers includes rational and irrational numbers, which can be positive, negative, or zero.
- ↑ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer, (New York: Wiley, 2000, ISBN 0471393401), 392, Fig. 24.61.
- ↑ Number 1! High School Math. Retrieved October 7, 2022.
- ↑ Harold Lindsell (ed.), Harper Study Bible: The Holy Bible Revised Standard Version (Grand Rapids, MI: Zondervan Bible Publishers, 1971).
ReferencesISBN links support NWE through referral fees
- Flegg, Graham. Numbers: Their History and Meaning. Mineola, NY: Dover Publications, 2002. ISBN 0486421651
- Ifrah, Georges. The Universal History of Numbers: From Prehistory to the Invention of the Computer. Translated by David Bellos et al. New York: Wiley, 2000. ISBN 0471393401
- Lindsell, Harold (ed.). Harper Study Bible: The Holy Bible Revised Standard Version. Grand Rapids, MI: Zondervan Bible Publishers, 1971.
- McLeish, John. The Story of Numbers: How Mathematics Has Shaped Civilization. New York: Fawcett Columbine, 1994. ISBN 0449909387
- Menninger, Karl. Number Words and Number Symbols: A Cultural History of Numbers. New York: Dover Publications, 1992. ISBN 0486270963
- Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. Rev. ed. London, UK: Penguin Books, 1998. ISBN 0140261494
External links
All links retrieved June 13, 2023.
- Number 1! High School Math.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.