Francis Ysidro Edgeworth

Francis Y. Edgeworth

Francis Ysidro Edgeworth (February 8, 1845 – February 13, 1926) was an Irish polymath, a highly influential figure in the development of neo-classical economics, and contributor to the development of statistical theory. He was the first to apply certain formal mathematical techniques to individual decision making in economics. Edgeworth developed utility theory, introducing the indifference curve and the famous "Edgeworth box," which have become standards in economic theory. He is also known for the "Edgeworth conjecture" which states that the core of an economy shrinks to the set of competitive equilibria as the number of agents in the economy gets large. The high degree of originality demonstrated in his most important book on economics, Mathematical Psychics, was matched only by the difficulty in reading it. A deep thinker, his contributions were far ahead of his time and continue to inform the fields of microeconomics and areas such as welfare economics. Thus, Edgeworth's work has advanced our understanding of economic relationships among traders, and thus contributes to the establishment of a better society for all.

Life

Ysidro Francis Edgeworth (the order of his given names was later reversed) was born on February 8, 1845 in Edgeworthstown, Ireland, into a large and wealthy landowning family. His aunt was the famous novelist Maria Edgeworth, who wrote the Castle Rackrent. He was educated by private tutors until 1862, when he went on to study classics and languages at Trinity College, Dublin. In 1867 he enrolled in the University of Oxford, where he obtained his degree in 1869 in Literae Humaniores.

In the 1870s, Edgeworth moved to Hempstead, near London. He lived on a private income, and continued to study. He finished law school, and in 1877 was called to the bar by the Inner Temple. He also studied mathematics and statistics on his own. It is probable that he became interested in economics through his Hempstead neighbor, William Stanley Jevons.

Edgeworth published his first book, New and Old Methods of Ethics in 1877, followed by several minor papers. He made money by lecturing on a wide variety of topics, from Greek language and English theater, to logic and mathematics. He tried several times to secure a more prestigious position at a university without success.

In 1881 he published his most famous book, Mathematical Psychics, in which he introduced several new concepts, including "Edgeworth's conjecture" and the "indifference curve." His writing demonstrated a high degree of originality, matched only by the difficulty of reading it, as he frequently referenced literary sources and interspersed the writing with passages in a number of languages, including Latin, French, and Ancient Greek as well as assuming mathematical proficiency on the part of the reader. The book initially received a lukewarm welcome, but influenced Alfred Marshall in writing his own Principles in 1890.

Edgeworth turned his interest to statistics and probability theory, writing in 1885 his Metretike. With this work, he finally received academic recognition, and was elected President of Section F of the British Association for the Advancement of Science in 1889.

In 1888, he was elected to the Tooke Chair in Economic Sciences and Statistics and King's College, London, and in 1891 the Drummond Professor and Fellow of All-Soul's College in Oxford. He held the latter position until his retirement.

In 1891, Edgeworth became the editor of the Economic Journal, the main publication of the British Economic Association. He served in this position until 1911, when he was succeeded by John Maynard Keynes. He again became editor in 1919, when Keynes became too busy with other duties, and continued in this role until his death.

In 1897, he published a survey of taxation, where he introduced his famous "taxation paradox," and in the early 1900s he focused on a critique of the marginal productivity theory. He wrote the article on probability in the 1911 edition of the Encyclopædia Britannica, and served as the President of the Royal Statistical Society from 1912 to 1914. During World War I, he wrote on war finances.

Edgeworth became the sole heir to his family's wealth in 1911, after his four older brothers died. He never married, although he attempted to court Beatrice Potter, the famous Fabian Socialist. Edgeworth died in 1926 in Oxfordshire, England.

Work

Edgeworth published his Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences in 1881, which became his most famous and original book. It was here that he presented his theory of economics. He attempted to apply mathematical principles to various social phenomena, including the capacity for happiness and the capacity for work. He concluded that women have less capacity for pleasure, and less capacity for work than men. This work introduced his famous Edgeworth conjecture, the Edgeworth box, and the Edgeworth theorem.

In Mathematical Psychics he also criticized William Stanley Jevons's theory of barter exchange, showing that under a system of "recontracting" there will be, in fact, many solutions, an "indeterminacy of contract." Edgeworth's "range of final settlements" was later resurrected by Martin Shubik as the game-theoretic concept of "the core."

One of the most influential economists of the time, Alfred Marshall, commented in his review of Mathematical Psychics:

This book shows clear signs of genius, and is a promise of great things to come... His readers may sometimes wish that he had kept his work by him a little longer till he had worked it out a little more fully, and obtained that simplicity which comes only through long labour. But taking it as what it claims to be, 'a tentative study', we can only admire its brilliancy, force, and originality (Marshall 1881).

While Jevons noted:

Whatever else readers of this book may think about it, they would probably all agree that it is a very remarkable one... There can be no doubt that in the style of his composition Mr. Edgeworth does not do justice to his matter. His style, if not obscure, is implicit, so that the reader is left to puzzle out every important sentence like an enigma (Jevons 1881).

In 1897, in an article on monopoly pricing, Edgeworth criticized Cournot's exact solution to the duopoly problem with quantity adjustments as well as Bertrand's "instantly competitive" result in a duopoly model with price adjustment. At the same time, Edgeworth showed how price competition between two firms with capacity constraints and/or rising marginal cost curves resulted in indeterminacy.

Edgeworth set the utilitarian foundations for highly progressive taxation, arguing that the optimal distribution of taxes should be such that "the marginal disutility incurred by each taxpayer should be the same" (Edgeworth, 1897). He presented the paradox that taxation of a commodity may actually result in a decrease in price. The economists of his time disregarded Edgeworth’s taxation paradox as a “mistake,” but more than thirty years later, Harold Hotelling (1932) rigorously proved that Edgeworth had been right.

Edgeworth's work in economics was not widely accepted in his lifetime, but as editor of the Economic Journal he was a prodigious reviewer of other works in economics. In this role he was a staunch defender of Marshall's views and thus greatly contributed to the dominance of his views in Britain in the early twentieth century.

Edgeworth conjecture

Edgeworth argued that as the number of subjects in an economy increases, the degree of indeterminacy is reduced. In the case of perfect competition, where there is an infinite number of subjects, the contract becomes identical to the "equilibrium" of economists. However, perfect competition is almost impossible to meet in the real world:

Equilibrium is attained when the existing contracts can neither be varied without recontract with the consent of the existing parties, nor by recontract within the field of competition. The advantage of this general method is that it is applicable to the particular case of imperfect competition where the conceptions of demand and supply at a price are no longer appropriate" (Edgeworth 1881 p.31).

The only way of resolving indeterminacy of contract then is to appeal to the utilitarian principle of maximizing the sum of the utilities of traders over the range of final settlements. Thus, Edgeworth introduced into economics the generalized utility function, U(x, y, z, ...), and the "indifference curve."

Edgeworth Box

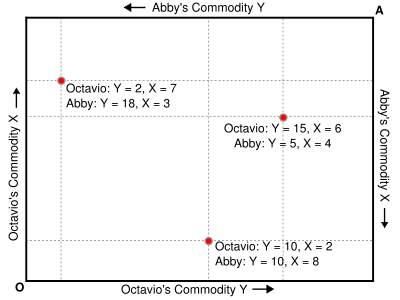
The Edgeworth Box is a way of representing various distributions of economic resources. It is a rectangular diagram with Subject A's Origin on one corner, and Subject B's origin on the opposite corner. The width of the box is the total amount of one commodity, and the height is the total amount of the other commodity. Thus, every possible division of the goods between the two people can be represented as a point in the box. If we draw among points in Edgeworth's Box, we obtain indifference curves, representing combinations of the goods that are of equal value for both Subject A and Subject B. Edgeworth's original two axis depiction was developed into the now familiar box diagram by Pareto in 1906, and was popularized in a later exposition by Arthur Lyon Bowley.

Imagine two people (Octavio and Abby) with a fixed amount of resources between the two of them — say, 10 liters of water and 20 hamburgers. If Octavio takes 5 hamburgers and 4 liters of water, then Abby is left with 15 hamburgers and 6 liters of water. The Edgeworth box is a rectangular diagram with Octavio's origin on one corner (represented by the O) and Abby's origin on the opposite corner (represented by the A). The width of the box is the total amount of one good, and the height is the total amount of the other good. Thus, every possible division of the goods between the two people can be represented as a point in the box.

In theory, it is possible to draw among these points indifference curves for both Abby and Octavio representing combinations of the goods that are of equal value, respectively, to Octavio and Abby. For example, Abby might value 1 liter of water and 13 hamburgers the same as 5 liters of water and 4 hamburgers, or 3 liters and 10 hamburgers. There is, of course, an infinity of such curves (assuming water and hamburgers to be infinitely divisible) that could be drawn among the combinations of goods for either consumer (Octavio or Abby).

Wherever one of these curves for Abby happens to just touch (but not cross) a curve of Octavio's, a unique combination of the two goods is identified that yields both consumers a maximum value. Such tangential contacts between the infinity of indifference-curve pairs, if plotted, will form a trace connecting Octavio's origin (O) to Abby's (A). The curve connecting points O and A is often called the contract curve.

Edgeworth limit theorem

Edgeworth's limit theorem examines the range of possible outcomes which may result from free market exchange or barter between groups of people. It shows that while the precise location of the final settlement (the ultimate division of goods) between the parties is indeterminate, there is a range of potential outcomes which shrinks as the number of traders increases. Edgeworth used a variant of what is now known as the Edgeworth box (with quantities traded, rather than quantities possessed, on the relevant axes) to analyze trade between groups of traders of various sizes. In general he found that "Contract without competition is indeterminate, contract with perfect competition is perfectly determinate, [and] contract with more or less perfect competition is less or more indeterminate" (Edgeworth 1881).

If trade in two goods, X and Y, occurs between a single pair of traders, A and B, the potential outcomes of this trade can be shown in an Edgeworth box. This is Edgeworth's key finding—the result of trade between two people can be predicted within a certain range but the exact outcome is indeterminate. This finding was (erroneously) disputed by Alfred Marshall and the discussions between the two on this point is known as the "barter controversy."

If there is a sufficient number of traders, the core of the market will shrink such that the point of final settlement is perfectly determinate. This point is equal to the price-taking equilibrium at which trade is assumed to take place at in models of perfect competition.

There are two main implications of the limit theorem. The first is that the end result of trade between small groups of people is indeterminate and is determined by what were to Edgeworth non-economic factors. The second is that the equivalent of a price-taking equilibrium can arise from competition between very large groups of traders through the recontracting process. This equilibrium point cannot be moved by groups of traders acting in collusion to try and obtain the gains from trade for themselves as other traders will always have an incentive to leave the group out in the cold. This provides a justification for assuming price-taking behavior in certain situations, even though explanations of how a price-taking situation can arise (such as Leon Walras' tâtonnement) are clearly implausible.

This analysis can be modified to accommodate traders who are not identical or who have motivations which aren't purely selfish as well as the situation where one group of traders is larger than the other. If the traders are heterogeneous the point P will not reflect a "split the difference" trade between the group of traders and the outer limit of trade determined by this point will be modified accordingly. If the utility of one trader(s) influences the utility of another (the latter is not selfish) then the associated limit of the contract curve will shrink inwards, ruling out the most inequitable trades. If the groups of traders are differently sized, the outer limits of the contract curve will not shrink an equal amount.

To a large degree the indeterminacy result relies on the assumption that the results of bargaining are indeterminate or, at the very least, outside the realm of economic speculation. Advances in game theory, such as those developed by John F. Nash, challenge this assumption and derive stable equilibria (such as the Nash equilibrium) in complicated bargaining situations. Further, Edgeworth's proposed recontracting process is highly stylized, involving traders obtaining information by making, breaking, and re-making contracts with each other without cost. Marshall strongly criticized Edgeworth on this point.

Legacy

Though Edgeworth's ideas were original and showed remarkable depth of thought, his manner of expression was not comprehensible to most of his contemporaries. Being well trained in languages and the classics, his words were long, intricate and erudite, not to mention the numerous obscure classical and literary references accompanying them.

Edgeworth was often regarded as “Marshall's man," referring to his support of Alfred Marshall. It was Edgeworth who greatly contributed toward the establishment of the Marshallian Neoclassical hegemony and the decline of any alternative approach.

Edgeworth himself never managed to attract any significant number of followers, thus never forming a school of thought. He was nevertheless respected by various economists, including Arthur Bowley, W.E. Johnson, Irving Fisher, Knut Wicksell, and Vilfredo Pareto. Pareto’s followers, Harold Hotelling and Abba Lerner, revived interest in Edgeworth again in the 1930s. In the 1960s and 1970s, as interest in mathematical economics flourished, Edgeworth’s works again became the center of academic curiosity. A group of mathematical economists, led by Herbert Scarf, Werner Hildenbrand, Martin Shubik, Gérard Debreu, and Robert Aumann, formed an "Edgeworthian" school of thought.

While apparently not particularly successful in his lifetime in terms of academic or public acclaim, Edgeworth left a warm impression on those who knew him. As noted in his obituary in The Times:

To a courtly grace, derived perhaps from his Spanish mother, he added the Irish characteristics of humour, imagination and generosity. A lifelong friend has never known him to be out of temper or speak ill words of others. In his sweetness and light were well combined. He was the merriest of men, and seemed to possess the secret of perpetual youth, both of mind and of body.

Works

Edgeworth, Francis Y. 1877. New and Old Methods of Ethics, or "Physical ethics" and "Methods of ethics". Oxford: J. Parker.
Edgeworth, Francis Y. 1879. The Hedonical Calculus. Mind, 4(15), 394-408.
Edgeworth, Francis Y. 1904. The Theory of Distribution. The Quarterly Journal of Economics, 2.
Edgeworth, Francis Y. 1884. The Rationale of Exchange. Journal of Royal Statistical Society, 47, 165-6.
Edgeworth, Francis Y. 1887. Metretike, or the method of measuring probability and utility. The Temple Co
Edgeworth, Francis Y. 1889. On the Application of Mathematics to Political Economy. Address of the President of Section F of the British Association for the Advancement of Science.
Edgeworth, Francis Y. 1894. The asymmetrical probability curve. Harrison and Sons.
Edgeworth, Francis Y. 1894. Theory of International Values: Parts I, II and III. Economic Journal
Edgeworth, Francis Y. 1915. On the Relations of Political Economy to War. London: Oxford University Press, H. Milford.
Edgeworth, Francis Y. 1918. Currency and Finance in Time of War. London: Oxford University Press, H. Milford
Edgeworth, Francis Y. 1925. Papers Relating to Political Economy (3 Vols.). Macmillan
Edgeworth, Francis Y. 1981 (original published in 1881). Mathematical Psychics: An essay on the application of mathematics to the moral sciences. Augustus M Kelley Pubs. ISBN 0678003084

References
ISBN links support NWE through referral fees

Blaug, Mark. 1992. Alfred Marshall and Francis Edgeworth. Edward Elgar Pub. ISBN 185278492X
Creedy, J. 1999. Development of the Theory of Exchange. The University of Melbourne, Department of Economics, Research Paper No. 605: 45.
Edgeworth, Maria. 2006. Castle Rackrent. 1st World Library. ISBN 1421803712
Fitzpatrick, P. J. 1960. Leading British statisticians of the nineteenth century. Journal of the American Statistical Association 55, 38-70.
Friel, Charles M. Biographies of Statisticians: Francis Edgeworth. Sam Houston State University. Retrieved on February 22, 2007,
Gilles, Robert P. 2005. Economic exchange and social organization: the Edgeworthian foundations of general equilibrium theory. Springer. ISBN 0792342003
Keynes, John Maynard. 1926. Francis Ysidro Edgeworth, 1845-1926: A memoir. London: Royal Economic Society.
Kendall, M.G. 1968. Francis Ysidro Edgeworth, 1845-1926. Biometrika, 55, 269-275.
NewSchool.edu Francis Ysidro Edgeworth.
Spiegel, Henry W. 1991. The Growth of Economic Thought. Ed. Durham & London. Duke University Press.
Marshall, Alfred. 1881. "Review of Mathematical Psychics" in The Academy, June 18, 1881, 457.
Jevons, William Stanley. 1881. "Review of Edgeworth's Mathematical Psychics" in Mind, Vol. 6, 581-583.
O'Connor, J.J. and E.F. Robertson. 2003. Francis Ysidro Edgeworth. JOC/EFR, 2003. Retrieved March 15, 2007.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

The history of this article since it was imported to New World Encyclopedia:

History of "Francis Ysidro Edgeworth"

Note: Some restrictions may apply to use of individual images which are separately licensed.