Fluid dynamics

Continuum mechanics

Conservation of mass Conservation of momentum Navier–Stokes equations Tensors Solid mechanics Solids · Stress · Deformation · Finite strain theory · Infinitesimal strain theory · Elasticity · Linear elasticity · Plasticity · Viscoelasticity · Hooke's law · Rheology Fluid mechanics Fluids · Fluid statics Fluid dynamics · Viscosity · Newtonian fluids Non-Newtonian fluids Surface tension Scientists Newton · Stokes · Navier · Cauchy· Hooke

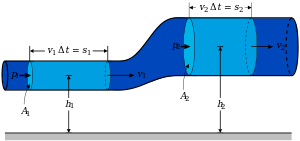
Fluid dynamics is the subdiscipline of fluid mechanics dealing with fluids (liquids and gases) in motion. It is itself divided into several subdisciplines, including aerodynamics (the study of gases in motion) and hydrodynamics (the study of liquids in motion). To solve a problem in fluid dynamics, the researcher needs to take into account various properties of the fluid, such as velocity, pressure, density, and temperature, as functions of space and time. The researcher then applies certain empirical and semi-empirical laws to calculate the flow of the fluid and the effects of the flow on objects in contact with the fluid.

In this typical aerodynamic teardrop shape, the pressure distribution is shown by the thickness of the black line, and the velocity in the boundary layer is shown by the violet triangles. The green vortex generators prompt the transition to turbulent flow and prevent back-flow (also called flow separation) from the high-pressure region in the back. The surface in front is as smooth as possible, as any turbulence here will reduce the energy of the airflow. The Kammback (abrupt cutoff of the taper in the back) also prevents back flow.

Fluid dynamics offers a systematic theoretical structure that underlies a wide range of practical applications. Examples include calculation of the forces and moments on aircraft, determination of the mass flow rate of petroleum through pipelines, prediction of weather patterns, understanding nebulae in interstellar space, and (reportedly) modeling the detonation of fission weapons. Some of the principles of fluid dynamics are even used in traffic engineering, where traffic is treated as a continuous fluid.

Foundational axioms and assumptions

The foundational axioms of fluid dynamics are the conservation laws:

• conservation of mass;
• conservation of momentum (also known as Newton's Second Law of Motion); and
• conservation of energy (also known as the First Law of Thermodynamics).

These laws are based on classical mechanics and are modified in quantum mechanics and general relativity. They are expressed using the Reynolds transport theorem.

In addition to the above axioms, fluids are assumed to obey the continuum assumption. Fluids are composed of molecules that collide with one another and solid objects. However, in the continuum assumption, fluids are regarded as continuous rather than discrete. Consequently, properties such as density, pressure, temperature, and velocity are taken to be well-defined at infinitely small points, and they are assumed to vary continuously from one point to another. The fact that the fluid is made up of discrete molecules is ignored.

For fluids that are sufficiently dense to be a continuum, do not contain ionized species, and have low velocities relative to the speed of light, the momentum equations for Newtonian fluids are the Navier-Stokes equations. These are non-linear differential equations that describe the flow of a fluid whose stress depends linearly on velocity and pressure.

The unsimplified equations do not have a general closed-form solution, so they are useful only in computational fluid dynamics or when they can be simplified. The equations can be simplified in a number of ways, all of which make them easier to solve. Some of them allow appropriate fluid dynamics problems to be solved in closed form.

In addition to the mass, momentum, and energy conservation equations, a thermodynamical equation of state giving the pressure as a function of other thermodynamic variables for the fluid is required to completely specify the problem. An example of this is the ideal gas law:

$p={\frac {\rho R_{u}T}{M}}$

where $p$ is pressure, $\rho$ is density, $R_{u}$ is the gas constant, $M$ is the molecular mass and $T$ is temperature.

Compressible vs incompressible flow

All fluids are compressible to some extent—that is, changes in pressure or temperature will result in changes in density. However, in many situations the changes in pressure and temperature are so small that the changes in density are negligible. In such cases, the flow can be modeled as an incompressible flow. Otherwise, the more general compressible flow equations must be used.

Mathematically, incompressibility is expressed by saying that the density $\rho$ of a fluid parcel does not change as it moves in the flow. In mathematical terms:

${\frac {\mathrm {D} \rho }{\mathrm {D} t}}=0\,,$

where $\mathrm {D} /\mathrm {D} t$ is the convective derivative. This additional constraint simplifies the governing equations, especially when the fluid has a uniform density.

For the flow of gases, to determine whether to use compressible or incompressible fluid dynamics, the Mach number of the problem is determined. As a rough guide, compressible effects can be ignored at Mach numbers below approximately 0.3. For liquids, whether the incompressible assumption is valid depends on the fluid properties (specifically the critical pressure and temperature of the fluid) and the flow conditions (how close to the critical pressure the actual flow pressure becomes).

Acoustic problems always require allowing compressibility, because sound waves are compression waves involving changes in pressure and density of the medium through which they propagate.

Viscous vs inviscid flow

Viscous problems are those in which fluid friction has significant effects on the solution. The Reynolds number can be used to evaluate whether viscous or inviscid equations are appropriate to the problem. Stokes flow is flow at very low Reynolds numbers, such that inertial forces can be neglected compared to viscous forces.

On the other hand, high Reynolds numbers indicate that the inertial forces are more significant than the viscous (friction) forces. Therefore, we may assume the flow to be an inviscid flow, an approximation in which we neglect viscosity, compared to the inertial terms.

This idea can work fairly well when the Reynolds number is high, even if certain problems, such as those involving boundaries, may require that viscosity be included. Viscosity often cannot be neglected near boundaries because the no-slip condition can generate a region of large strain rate (a boundary layer) that enhances the effect of even a small amount of viscosity, generating vorticity.

Consequently, to calculate net forces on bodies (such as wings), we should use viscous equations. As illustrated by d'Alembert's paradox, a body in an inviscid fluid will experience no force. The standard equations of inviscid flow are the Euler equations.

Another model, often used in computational fluid dynamics, is to use the Euler equations for flow far from the body, and the boundary layer equations, which incorporate viscosity, for flow close to the body.

Steady vs unsteady flow

When all time derivatives of a flow field vanish, the flow is considered steady. Otherwise, it is called unsteady. Whether a particular flow is steady or unsteady can depend on the chosen frame of reference. For instance, laminar flow over a sphere is steady in the frame of reference that is stationary with respect to the sphere. In a frame of reference that is stationary with respect to the background flow, the flow is unsteady.

Turbulent flows are unsteady by definition. A turbulent flow can, however, be statistically stationary. According to Pope, "The random field U(x,t) is statistically stationary if all statistics are invariant under a shift in time" (Pope 2000, 75)—in other words, the statistical properties do not change over time. Often, the mean field is the object of interest, and this is constant in a statistically stationary flow.

Steady flows are often more tractable than otherwise similar unsteady flows. The governing equations of a steady problem have one dimension less (time) than the governing equations of the same problem without taking advantage of the steadiness of the flow field.

Although time-periodic problems are strictly unsteady flows, they can often be solved by the same techniques as steady flows. For this reason, they can be considered somewhere between steady and unsteady flows.

Laminar vs turbulent flow

Turbulence is flow dominated by recirculation, eddies, and apparent randomness. Flow in which turbulence is not exhibited is called laminar. It should be noted, however, that the presence of eddies or recirculation does not necessarily indicate turbulent flow—these phenomena may be present in laminar flow as well. Mathematically, turbulent flow is often represented via Reynolds decomposition, in which the flow is broken down into the sum of a steady component and a perturbation component.

It is believed that turbulent flows obey the Navier-Stokes equations. A method called direct numerical simulation (DNS), based on the incompressible Navier-Stokes equations, makes it possible to simulate turbulent flows with moderate Reynolds numbers. (Restrictions depend on computer power and efficiency of the solution algorithm). The results of DNS agree with experimental data.

Most flows of interest have Reynolds numbers too high for DNS to be a viable option, given the state of computational power for the next few decades (Pope 2000). Any flight vehicle large enough to carry a human (vehicle length greater than three meters), moving faster than 72 km/h (20 m/s) is well beyond the DNS limit (Re = four million). For example, transport aircraft wings (such as on an Airbus A300 or Boeing 747) have Reynolds numbers of 40 million (based on the wing chord).

To solve these real-life flow problems, turbulence models will be a necessity for the foreseeable future. Large eddy simulation also holds promise as a simulation methodology, especially in the form of detached eddy simulation (DES), which is a combination of turbulence modeling and large eddy simulation.

Newtonian vs non-Newtonian fluids

Sir Isaac Newton showed how stress and the rate of change of strain are very close to a linear relationship for many familiar fluids, such as water and air. These Newtonian fluids are modeled by a coefficient called viscosity, which depends on the specific fluid.

However, some other materials—such as emulsions, slurries. and some visco-elastic materials (for example, blood or some polymers)—have more complicated non-Newtonian stress-strain behavior. These materials include sticky liquids such as latex, honey, and lubricants, which are studied in the sub-discipline of rheology.

Additional approximations

There are many other possible approximations for fluid dynamic problems. Some common examples are listed below.

• The Boussinesq approximation neglects variations in density, except to calculate buoyancy forces. It is often used in free convection problems where density changes are small.
• Lubrication theory exploits the large aspect ratio of the domain to show that certain terms in the equations are small and can therefore be neglected.
• Slender-body theory is a methodology used in Stokes flow problems to estimate the force on, or flow field around, a long, slender object in a viscous fluid.
• Shallow-water equations can be used to describe a layer of relatively inviscid fluid with a free surface, in which surface gradients are small.
• Darcy's law is used for flows in porous media. It works with variables averaged over several pore-widths.
• In rotating systems, the quasi-geostrophic approximation assumes an almost perfect balance between pressure gradients and the Coriolis force. It is useful in the study of atmospheric dynamics.

See also

• Acoustics
• Aerodynamics
• Aeronautics
• Density
• Fluid
• Gas
• Hydraulics
• Hydrology
• Liquid
• Materials science
• Meteorology
• Oceanography
• Pressure
• Pump
• Quantum hydrodynamics
• Rheology
• Statics
• Superfluidity
• Surface tension
• Thermodynamics
• Vapor pressure
• Viscosity

References

ISBN links support NWE through referral fees

• Acheson, D. J. 1990. Elementary Fluid Dynamics. Oxford Applied Mathematics and Computing Science Series. Oxford: Clarendon Press.
• Batchelor, G. K. 1967. An Introduction to Fluid Dynamics. Cambridge: Cambridge University Press. OCLC 421665
• Fox, Robert W., Alan T. McDonald, and Philip J. Pritchard. 2006. Introduction to Fluid Mechanics. 2006 just ask! edition. Hoboken, NJ: John Wiley. ISBN 978-0471735588
• Landau, L. D., and E. M. Lifshitz. 1959. Fluid Mechanics. London: Pergamon Press. OCLC 536434
• Pope, S. B. 2000. Turbulent Flows. Cambridge: Cambridge University Press. ISBN 9780521598866
• Shinbrot, Marvin. 1973. Lectures on Fluid Mechanics. Notes on mathematics and its applications. New York: Gordon and Breach. ISBN 9780677017150
• White, Frank M. 2007. Fluid Mechanics, 6th ed. New York: McGraw-Hill. ISBN 978-0071286466

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Fluid dynamics  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Fluid dynamics"

Note: Some restrictions may apply to use of individual images which are separately licensed.