Game theory
Game theory is a branch of applied mathematics comprising a family of mathematical models used for strategic analysis of interactions involving two or more interdependent agents or "players" each pursuing an independent self-interest while trying to take into account the effects of decisions made by the other players. First developed as a mathematical theory of economic and social organization based on a theory of games of strategy, as explained in the 1944 classic book Theory of Games and Economic Behavior by John von Neumann and Oskar Morgenstern, game theory was soon applied by the RAND Corporation for developing nuclear strategies. The theory has subsequently proven to be relevant in such diverse academic fields as biology, psychology, sociology, and philosophy. Many game theoretic models, especially the prisoner's dilemma in which rational self-interest hurts all the players, are used to illustrate ideas in political science, ethics, and philosophy. Most recently, computer scientists have applied models from game theory in the fields of artificial intelligence and cybernetics.
The 1994 Nobel Prize in Economics recognized the work of three men in advancing the understanding of how game theory applies to certain types of economic or social situations. One of those co-winners was the mathematician John Nash who subsequently was the subject of the 1998 biography by Sylvia Nasar and the 2001 film A Beautiful Mind. Game theory was also a theme in the 1983 film WarGames. Several game shows have adopted game theoretic situations, including Friend or Foe? and to some extent Survivor. The character Jack Bristow on the television show Alias is one of the few fictional game theorists in popular culture. Another popular television program involving game theory is the crime drama Numb3rs.
The key premise of game theory—that the actors in the interaction are each pursuing their own "rational self-interest" in a way that affects the outcome of the other actors' decisions—accurately mirrors the sense of human identity common in much of the modern, Western world. In this sense of identity each person is a separate, independent entity whose ties to other people, if at all, are primarily some kind of externally-imposed obligatory interdependence. Such a sense of human identity contrasts with that of many religious people, primitive peoples, and much of the traditional Eastern world in which each person is integrally part of some larger fabric, such as community, society, or the natural world, that collectively fulfills some common purpose. While some types of game theory are called cooperative, the term in such cases usually refers to cooperation pursued due to constraint or self-interested motivation. Enduring peaceful resolution of many of the global issues facing humanity today may not be contained within the conceptual framework of today's game theory.
Representation of games
The games studied by game theory are well-defined mathematical objects comprising a set of players, a set of strategies available to those players, and a specification of payoffs for each combination of strategies. Two ways of representing games are common in the literature.
Normal form
| Player 2 chooses left | Player 2 chooses right | |
|---|---|---|
| Player 1 chooses top | 4, 3 | -1, -1 |
| Player 1 chooses bottom | 0, 0 | 3, 4 |
The normal (or strategic) form game is a matrix which shows the players, strategies, and payoffs (see the example to the right). Here there are two players; one chooses the row and the other chooses the column. Each player can choose one of two strategies, which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the row player (Player 1 in the example); the second is the payoff for the column player (Player 2 in the example). Suppose that Player 1 plays top and that Player 2 plays left. Then Player 1 gets 4, and Player 2 gets 3.
When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form.
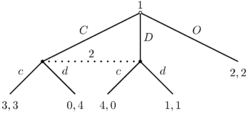
Extensive form
The extensive form can be used to formalize games with some important order. Games here are presented as trees (as pictured to the left). Here each vertex (or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree.
In the game pictured here, there are two players. Player 1 moves first and chooses either F or U. Player 2 sees Player 1's move and then chooses A or R. Suppose that Player 1 chooses U and then Player 2 chooses A, then Player 1 gets 8 and Player 2 gets 2.
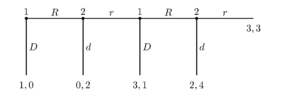
The extensive form can also capture simultaneous-move games. Either a dotted line or circle is drawn around two different vertices to represent them as being part of the same information set (i.e., the players do not know at which point they are).
Types of games
Symmetric and asymmetric
| E | F | |
|---|---|---|
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
A symmetric game is a game in which the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If the identities of the players can be changed without changing the payoff to the strategies, then a game is symmetric. Many of the commonly studied 2×2 games are symmetric. The standard representations of chicken, the prisoner's dilemma, and the stag hunt are all symmetric games. Some scholars would consider certain asymmetric games as examples of these games as well. However, the most common payoffs for each of these games are symmetric.
In most of the commonly studied asymmetric games the strategy sets for the players are not identical. For instance, the ultimatum game and similarly the dictator game have a different strategy for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric. For example, the game pictured to the right is asymmetric despite having identical strategy sets for both players.
Zero sum and non-zero sum
| A | B | |
|---|---|---|
| A | 2, −2 | −1, 1 |
| B | −1, 1 | 3, −3 |
In zero-sum games the total benefit to all players in the game, for every combination of strategies, always adds to zero (or more informally put, a player benefits only at the expense of others). Poker exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero sum games include matching pennies and most classical board games including go and chess. Many games studied by game theorists (including the famous prisoner's dilemma) are non-zero-sum games, because some outcomes have net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.
It is possible to transform any game into a zero-sum game by adding an additional dummy player (often called "the board"), whose losses compensate the players' net winnings.
Simultaneous and sequential
Simultaneous games require either that both players move simultaneously, or, if they do not move simultaneously, that the later players are unaware of the earlier players' actions (making the moves effectively simultaneous). In sequential games (or dynamic games) later players have some knowledge about earlier actions. This need not be perfect knowledge about every action of earlier players; it might be very little information. For instance, a player may know that an earlier player did not perform one particular action, while she does not know which of the remaining available actions the first player actually performed.
The difference between simultaneous and sequential games is captured in the different representations discussed above. Normal form is used to represent simultaneous games, and extensive form is used to represent sequential ones.
Perfect information and imperfect information
An important subset of sequential games consists of games of perfect information. A game is one of perfect information if all players know the moves previously made by all other players. Thus, only sequential games can be games of perfect information, since in simultaneous games not every player knows the actions of the others. Most games studied in game theory are perfect information games, although there are some interesting examples of imperfect information games, including the ultimatum game and centipede game. Perfect information games include chess, go, mancala, and arimaa.
Perfect information is often confused with complete information, which is a similar concept. Complete information requires that every player know the strategies and payoffs of the other players but not necessarily the actions.
Infinitely long games
For obvious reasons, games as studied by economists and real-world game players are generally finished in a finite number of moves. Pure mathematicians are not so constrained, and set theorists in particular study games that last for infinitely many moves, with the winner (or other payoff) not known until after all those moves are completed.
The focus of attention is usually not so much on what is the best way to play such a game, but simply on whether one or the other player has a winning strategy. (It can be proven, using the axiom of choice, that there are games—even with perfect information, and where the only outcomes are "win" or "lose"—for which neither player has a winning strategy.) The existence of such strategies, for cleverly designed games, has important consequences in descriptive set theory.
Uses of game theory
Games in one form or another are widely used in many different academic disciplines.
Economics and business
Economists have used game theory to analyze a wide array of economic phenomena, including auctions, bargaining, duopolies, oligopolies, social network formation, and voting systems. This research usually focuses on particular sets of strategies known as equilibria in games. These "solution concepts" are usually based on what is required by norms of rationality. The most famous of these is the Nash equilibrium. A set of strategies is a Nash equilibrium if each represents a best response to the other strategies. So, if all the players are playing the strategies in a Nash equilibrium, they have no incentive to deviate, since their strategy is the best they can do given what others are doing.
The payoffs of the game are generally taken to represent the utility of individual players. Often in modeling situations, the payoffs represent money, which presumably corresponds to an individual's utility. This assumption, however, can be faulty.
A prototypical paper on game theory in economics begins by presenting a game that is an abstraction of some particular economic situation. One or more solution concepts are chosen, and the author demonstrates which strategy sets in the presented game are equilibria of the appropriate type. Economists and business professors suggest two primary uses for game theory.
Descriptive
Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This particular view of game theory has come under recent criticism. First, because the assumptions made by game theorists are often violated. Game theorists may assume players always act rationally to maximize their wins (the Homo economicus model), but real humans often act either irrationally, or act rationally to maximize the wins of some larger group of people (altruism). Game theorists respond by comparing their assumptions to those used in physics. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific ideal akin to the models used by physicists. Further criticism of this use of game theory has been levied because some experiments have demonstrated that individuals do not play equilibrium strategies. For instance, in the Centipede game, Guess 2/3 of the average game, and the Dictator game, people regularly do not play by the Nash equilibria. There is an ongoing debate regarding the importance of these experiments.
Alternatively, some authors claim that Nash equilibria do not provide predictions for human populations, but rather provide an explanation for why populations that play Nash equilibria remain in that state. However, the question of how populations reach those points remains open.
Some game theorists have turned to evolutionary game theory in order to resolve these worries. These models presume either no rationality or bounded rationality on the part of players. Despite the name, evolutionary game theory does not necessarily presume natural selection in the biological sense. Evolutionary game theory includes both biological as well as cultural evolution and also models of individual learning (for example, fictitious play dynamics).
Normative
| Cooperate | Defect | |
|---|---|---|
| Cooperate | 2, 2 | 0, 3 |
| Defect | 3, 0 | 1, 1 |
On the other hand, some scholars see game theory not as a predictive tool for the behavior of human beings, but as a suggestion for how people ought to behave. Since a Nash equilibrium of a game constitutes one's best response to the actions of the other players, playing a strategy that is part of a Nash equilibrium seems appropriate. However, this use for game theory has also come under criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects others to play non-equilibrium strategies as well. For an example, see the Guess 2/3 of the average game.
Second, the Prisoner's Dilemma presents another potential counterexample. In the Prisoner's Dilemma, each player pursuing his own self-interest leads both players to be worse off than if they had not pursued their own self-interests. Some scholars believe that this demonstrates the failure of game theory as a recommendation for behavior.
Biology
| Hawk | Dove | |
|---|---|---|
| Hawk | (V-C)/2, (V-C)/2 | V, 0 |
| Dove | 0, V | V/2, V/2 |
Unlike payoffs for games in economics, the payoffs for games in biology are often interpreted as corresponding to fitness. In addition, the focus has been less on equilibria that correspond to a notion of rationality, but rather on ones that would be maintained by evolutionary forces. The most well-known equilibrium in biology, the Evolutionary stable strategy or (ESS), and was first introduced in 1982 by John Maynard Smith. Although its initial motivation did not involve any of the mental requirements of the Nash equilibrium, every ESS is a Nash equilibrium.
In biology, game theory has been used to understand many different phenomena. It was first used to explain the evolution (and stability) of the approximate 1:1 sex ratios. Ronald Fisher (1930) suggested that the 1:1 sex ratios are a result of evolutionary forces acting on individuals who could be seen as trying to maximize their number of grandchildren.
Additionally, biologists have used evolutionary game theory and the ESS to explain the emergence of animal communication (Maynard Smith & Harper, 2003). The analysis of signaling games and other communication games has provided some insight into the evolution of communication among animals.
Finally, biologists have used the hawk-dove game (also known as "chicken") to analyze fighting behavior and territoriality.
Computer science and logic
Game theory has come to play an increasingly important role in logic and in computer science. Several logical theories have a basis in game semantics. In addition, computer scientists have used games to model interactive computations.
Political science
Research in political science has also used game theory. A game-theoretic explanation for the democratic peace is that the public and open debates in democracies send clear and reliable information regarding the intentions to other states. In contrast, it is difficult to know the intentions of nondemocratic leaders, what effect concessions will have, and if promises will be kept. Thus there will be mistrust and unwillingness to make concessions if at least one of the parties in a dispute is a nondemocracy. Gilat Levy and Ronny Razin, 2003, It Takes Two: An Explanation of the Democratic Peace. Social Science Research Network. Retrieved July 12, 2007.
Philosophy
Game theory has been put to several uses in philosophy. Responding to two papers by W.V.O. Quine (1960, 1967), David Lewis (1969) used game theory to develop a philosophical account of convention. In so doing, he provided the first analysis of common knowledge and employed it in analyzing play in coordination games. In addition, he first suggested that one can understand meaning in terms of signaling games. This later suggestion has been pursued by several philosophers since Lewis (Skyrms 1996, Grim et al. 2004).
| Stag | Hare | |
|---|---|---|
| Stag | 3, 3 | 0, 2 |
| Hare | 2, 0 | 2, 2 |
In ethics, some authors have attempted to pursue the project, begun by Thomas Hobbes, of deriving morality from self-interest. Since games like the Prisoner's Dilemma present an apparent conflict between morality and self-interest, explaining why cooperation is required by self-interest is an important component of this project. This general strategy is a component of the general social contract view in political philosophy (for examples, see Gauthier 1987 and Kavka 1986). Bruno Verbeek and Christopher Morris, Game theory and ethics. Stanford Encyclopedia of Philosophy. Retrieved July 12, 2007.</ref>
Finally, other authors have attempted to use evolutionary game theory in order to explain the emergence of human attitudes about morality and corresponding animal behaviors. These authors look at several games including the Prisoner's Dilemma, Stag hunt, and the Nash bargaining game as providing an explanation for the emergence of attitudes about morality (see, e.g., Skyrms 1996, 2004; Sober and Wilson 1999).
Sociology
There are fewer applications of game theory in sociology than in its sister disciplines, political science and philosophy. However, a game theoretic analysis of interactions among prisoners was conducted by Kaminski (2004).
History of game theory
The issues dealt with in game theory were recognized and acted upon long before the origins of systematic mathematical consideration of those issues arose. Plato wrote in his dialogue Laches, for example, of Socrates's perceptive analysis of the rational choice options for soldiers facing an oncoming army. Much later, but still well before the origin of game theory, in a move that fits precisely into one response option mapped by game theory, the Spanish conquistador Cortes burned his ships barring any possibility that his small force of men could retreat under the threat of much larger numbers of Aztecs. The awestruck Aztecs reportedly retreated in the face of an act displaying such a presumption of power and Cortes went on to conquer the Aztec nation.
The first known discussion of game theory occurred in a letter written by James Waldegrave in 1713. In this letter, Waldegrave provides a minimax mixed strategy solution to a two-person version of the card game "le Her." It was not until the publication of Antoine Augustin Cournot's Researches into the Mathematical Principles of the Theory of Wealth in 1838 that a general game theoretic analysis was pursued. In this work Cournot considers a duopoly and presents a solution that is a restricted version of the Nash equilibrium.
Although Cournot's analysis is more general than Waldegrave's, game theory did not really exist as a unique field until John von Neumann published a series of papers in 1928. While the French mathematician Borel did some earlier work on games, von Neumann can rightfully be credited as the inventor of game theory. Von Neumann was a brilliant mathematician whose work was far-reaching—from set theory, to his calculations that were key to development of both the Atom and Hydrogen bombs, and finally to his work developing computers. Von Neumann's work culminated in the 1944 book, The Theory of Games and Economic Behavior, which he coauthored with Oskar Morgenstern. This profound work contains the method for finding optimal solutions for two-person zero-sum games. During this time period, work on game theory was primarily focused on cooperative game theory, which analyzes optimal strategies for groups of individuals, presuming that they can enforce agreements between them about proper strategies.
In 1950, the first discussion of the Prisoner's dilemma appeared, and an experiment was undertaken on this game at the RAND corporation. Around this same time, John Nash developed a definition of an "optimum" strategy for multiplayer games where no such optimum was previously defined, known as Nash equilibrium. This equilibrium is sufficiently general, allowing for the analysis of non-cooperative games in addition to cooperative ones.
Game theory experienced a flurry of activity in the 1950s, during which time the concepts of the core, the extensive form game, fictitious play, repeated games, and the Shapley value were developed. In addition, the first applications of Game theory to philosophy and political science occurred during this time.
In 1965, Reinhard Selten introduced his solution concept of subgame perfect equilibria, which further refined the Nash equilibrium (later he would introduce trembling hand perfection as well). In 1967, John Harsanyi developed the concepts of complete information and Bayesian games. He, along with John Nash and Reinhard Selten, won the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel in 1994.
In the 1970s, game theory was extensively applied in biology, largely as a result of the work of John Maynard Smith and his evolutionary stable strategy. In addition, the concepts of correlated equilibrium, trembling hand perfection, and common knowledge were introduced and analyzed.
In 2005, game theorists Thomas Schelling and Robert Aumann won the Bank of Sweden Prize in Economic Sciences. Schelling worked on dynamic models, early examples of evolutionary game theory. Aumann contributed more to the equilibrium school, developing an equilibrium coarsening correlated equilibrium and developing extensive analysis of the assumption of common knowledge.
ReferencesISBN links support NWE through referral fees
Textbooks and general reference texts
- Bierman, H. S. and L. Fernandez. Game Theory with economic applications. Addison-Wesley, 1998.
- Fudenberg, Drew and Jean Tirole. Game Theory. MIT Press, 1991. ISBN 0262061414
- Dutta, Prajit. Strategies and Games: Theory and Practice. MIT Press, 2000. ISBN 0262041693
- Gibbons, Robert. Game Theory for Applied Economists. Princeton University Press, 1992. ISBN 0691003955
- Gintis, Herbert. Game Theory Evolving. Princeton University Press, 2000. ISBN 0691009430
- Miller, James. Game Theory At Work. McGraw-Hill, 2003. ISBN 0071400206
- Osborne, Martin J. An Introduction to Game Theory. New York: Oxford University Press, 2004. ISBN 0195128958
- Osborne, Martin J. and Ariel Rubinstein. A Course in Game Theory. MIT Press, 1994. ISBN 0262650401
- Rasmusen, Eric. Games and information, 4th edition. Blackwell, 2006.
- Mas-Colell, Whinston and Green. Microeconomic Theory. Oxford University Press, 1995. ISBN 0195073401
Historically important texts
- Fisher, Ronald. The Genetical Theory of Natural Selection. Oxford: Clarendon Press, 1930.
- Luce, Duncan and Howard Raiffa. Games and Decisions: Introduction and Critical Survey. Dover. ISBN 0486659437
- Smith, John Maynard. Evolution and the Theory of Games. Cambridge University Press, 1982.
- Morgenstern, Oskar and John von Neumann. The Theory of Games and Economic Behavior. Princeton University Press, 1947.
- Nash, John. "Equilibrium points in n-person games," Proceedings of the National Academy of the USA 36(1) (1950):48-49.
- Poundstone, William. Prisoner's Dilemma: John von Neumann, Game Theory and the Puzzle of the Bomb. ISBN 038541580X
Other print references
- Camerer, Colin. Behavioral Game Theory. Princeton University Press, 2003. ISBN 0691090394
- Gauthier, David. Morals by Agreement Oxford University Press, 1987. ISBN 0198249926
- Grim, Patrick, Trina Kokalis, Ali Alai-Tafti, Nicholas Kilb, and Paul St Denis. (2004) "Making meaning happen." Journal of Experimental & Theoretical Artificial Intelligence 16(4): 209-243.
- Kaminski, Marek M. Games Prisoners Play. Princeton University Press, 2004. ISBN 0691117217
- Kavka, Gregory. Hobbesian Moral and Political Theory. Princeton University Press, 1986. ISBN 069102765X
- Lewis, David. Convention: A Philosophical Study. 1969.
- Smith, J. Maynard and D. Harper. Animal Signals. Oxford University Press, 2003. ISBN 0198526857
- Quine, W.V.O. "Truth by Convention" in Philosophica Essays for A.N. Whitehead Russel and Russel Publishers, 1967.
- Quine, W.v.O (1960) "Carnap and Logical Truth." Synthese 12(4):350-374.
- Skyrms, Brian. Evolution of the Social Contract. Cambridge University Press, 1996. ISBN 0521555833
- Skyrms, Brian. The Stag Hunt and the Evolution of Social Structure. Cambridge University Press, 2004. ISBN 0521533929.
- Sober, Elliot and David Sloan Wilson. Unto Others: The Evolution and Psychology of Unselfish Behavior. Harvard University Press, 1999. ISBN 0674930479
External links
All links retrieved April 17, 2024.
- David K. Levine: Economic and Game Theory.
- Mike Shor: " A resource for educators and students of game theory", GameTheory.net.
- Jim Ratliff: "Graduate-Level Course in Game Theory", virtualperfection.com.
- Game Theory. Stanford Encyclopedia of Philosophy.
- Game Theory and Ethics. Stanford Encyclopedia of Philosophy.
- Web sites on game theory and social interactions. Social Capital Gateway.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.