Main sequence
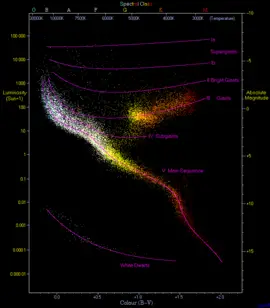
Main sequence is the class name for stars that occupy a continuous distinctive band formed by plotting stellar color versus brightness for a large sample of stars. These color-magnitude plots are known as Hertzsprung-Russell diagrams after their co-developers, Ejnar Hertzsprung and Henry Norris Russell. Main sequence stars are normal stars, but due to historical factors they are also known as dwarf stars. Other "dwarf" stars that are not main sequence stars include white dwarfs and brown dwarfs.
After a star has formed, it generates energy at its hot, dense core through the fusion of hydrogen atoms into helium. During this stage, the star is located along the main sequence at a position determined primarily by its mass, but also by its chemical composition and other factors. In general, the more massive the star, the shorter its time on the main sequence.
The main sequence is sometimes divided into upper and lower parts, based on the processes that stars use to generate energy. Stars below about 1.5 times the mass of the Sun (or 1.5 solar masses) fuse hydrogen atoms together in a series of stages to form helium, a sequence called the proton-proton chain. Above this mass, in the upper main sequence, the nuclear fusion process can instead use atoms of carbon, nitrogen, and oxygen as intermediaries in the production of helium from hydrogen atoms.
Astronomers' development and use of the Hertzsprung-Russell diagrams is a good example of one of the approaches used by scientists in their efforts to discover the underlying order and principles of the natural world. When faced with an abundance of data (such as the measurements and analysis of radiation from myriads of stars), scientists identify criteria (in this case, brightness and color) that seem significant, define the criteria in scientifically measurable terms (in this case, absolute magnitude and color index), plot the data on an appropriately scaled graph, and look for a pattern. In this case, the pattern is the main sequence, which has proven to be a valuable guide for theoreticians as they have developed conceptual and mathematical models of stellar evolution.
History
In the early part of the twentieth century, information about the types and distances of stars became more readily available. The spectra of stars were shown to have distinctive features, which allowed them to be categorized. Annie Jump Cannon and Edward C. Pickering at Harvard College Observatory had developed a method of categorization that became known as the Harvard classification scheme. This scheme was published in the Harvard Annals in 1901.[1]
In Potsdam in 1906, the Danish astronomer Ejnar Hertzsprung noticed that the reddest stars—classified as K and M in the Harvard scheme—could be divided into two distinct groups. These stars are either much brighter than the Sun, or much fainter. To distinguish these groups, he called them "giant" and "dwarf" stars. The following year he began studying star clusters; large groupings of stars that are co-located at approximately the same distance. He published the first plots of color versus luminosity for these stars. These plots showed a prominent and continuous sequence of stars, which he named the main sequence.[2]
At Princeton University, Henry Norris Russell was following a similar course of research. He was studying the relationship between the spectral classification of stars and their actual brightness as corrected for distance—their absolute magnitude. For this purpose he used a set of stars that had reliable parallaxes and many of which had been categorized at Harvard. When he plotted the spectral types of these stars against their absolute magnitude, he found that dwarf stars followed a distinct relationship. This allowed the real brightness of a dwarf star to be predicted with reasonable accuracy.[3]
Of the red stars observed by Hertzsprung, the dwarf stars also followed the spectra-luminosity relationship discovered by Russell. However, the giant stars are much brighter than dwarfs and so do not follow the same relationship. Russell proposed that the "giant stars must have low density or great surface-brightness, and the reverse is true of dwarf stars." The same curve also showed that there were very few faint white stars.[3]
In 1933, Bengt Strömgren introduced the term Hertzsprung-Russell diagram to denote a luminosity-spectral class diagram.[4] This name reflected the parallel development of this technique by both Hertzsprung and Russell earlier in the century.[2]
As evolutionary models of stars were developed during the 1930s, it was shown that, for stars of a uniform chemical composition, a relationship exists between a star's mass and its luminosity and radius. That is, for a given mass and composition is known, there is a unique solution determining the star's radius and luminosity. This became known as the Vogt-Russell theorem; named after Heinrich Vogt and Henry Norris Russell. By this theorem, once a star's chemical composition and its position on the main sequence is known, so too is the star's mass and radius. (However, it was subsequently discovered that the theorem breaks down somewhat for stars of non-uniform composition.)[5]
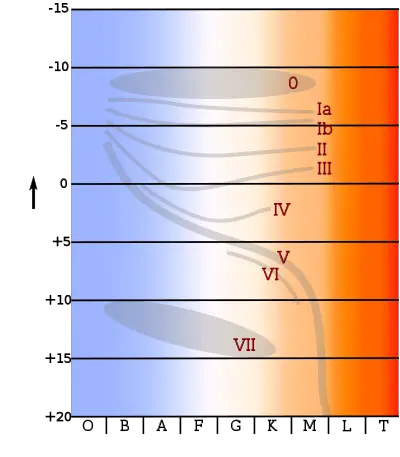
A refined scheme for stellar classification was published in 1943 by W. W. Morgan and P. C. Keenan.[6] The MK classification assigned each star a spectral type—based on the Harvard classification—and a luminosity class. For historical reasons, the spectral types of stars followed, in order of decreasing temperature with colors ranging from blue to red, the sequence O, B, A, F, G, K and M. (A popular mnemonic for memorizing this sequence of stellar classes is "Oh Be A Fine Girl/Guy, Kiss Me.") The luminosity class ranged from I to V, in order of decreasing luminosity. Stars of luminosity class V belonged to the main sequence.[7]
Formation
When a protostar is formed from the collapse of a giant molecular cloud of gas and dust in the local interstellar medium, the initial composition is homogeneous throughout, consisting of about 70% hydrogen, 28% helium and trace amounts of other elements, by mass.[8] During the initial collapse, this pre-main sequence star generates energy through gravitational contraction. Upon reaching a suitable density, energy generation is begun at the core using an exothermic nuclear fusion process that converts hydrogen into helium.[7]
Once nuclear fusion of hydrogen becomes the dominant energy production process and the excess energy gained from gravitational contraction has been lost,[9] the star lies along a curve on the Hertzsprung-Russell diagram (or HR diagram) called the standard main sequence. Astronomers will sometimes refer to this stage as "zero age main sequence," or ZAMS.[10] The ZAMS curve can be calculated using computer models of stellar properties at the point when stars begin hydrogen fusion. From this point, the brightness and surface temperature of stars typically increase with age.[11]
A star remains near its initial position on the main sequence until a significant amount of hydrogen in the core has been consumed, then begins to evolve into a more luminous star. (On the HR diagram, the evolving star moves up and to the right of the main sequence.) Thus the main sequence represents the primary hydrogen-burning stage of a star's lifetime.[7]
Properties
Main sequence stars have been extensively studied through stellar models, allowing their formation and evolutionary history to be relatively well understood. The position of the star on the main sequence provides information about its physical properties.
The majority of stars on a typical HR diagram lie along the main sequence curve. This line is so pronounced because both the spectral type and the luminosity depend only on a star's mass, at least to zeroth order approximation, as long as it is fusing hydrogen at its core—and that is what almost all stars spend most of their "active" life doing.[12] These main-sequence (and therefore "normal") stars are called dwarf stars. This is not because they are unusually small, but instead comes from their smaller radii and lower luminosity as compared to the other main category of stars, the giant stars.[13] White dwarfs are a different kind of star that are much smaller than main sequence stars—being roughly the size of the Earth. These represent the final evolutionary stage of many main sequence stars.[14]
The temperature of a star determines its spectral type, because the energy modifies the physical properties of the plasma in the photosphere. Both the temperature and composition determines the star's energy emission at different wavelengths. A key indicator of this energy distribution is given by the color index, B—V, which measures the star's magnitude in blue (B) and green-yellow (V) light by means of filters. (By measuring the difference between these values, one can eliminate the need to correct the magnitudes for distance.) Thus, this difference in magnitude provides a measure of a star's temperature.
Because there is a temperature gradient between the core of a star and its surface, energy is steadily transported upward through the intervening layers until it is radiated away at the photosphere. The two mechanisms used to carry this energy through the star are radiation and convection, with the type used depending on the local conditions. Convection tends to occur in regions with steeper temperature gradients, higher opacity or both. When convection occurs in the core region it acts to stir up the helium ashes, thus maintaining the proportion of fuel needed for fusion to occur.
By treating the star as an idealized energy radiator known as a black body, the luminosity L and radius R can be related to the effective temperature Teff by the Stefan–Boltzmann law:
where σ is the Stefan–Boltzmann constant. As the position of a star on the HR diagram shows its approximate luminosity, this relation can be used to estimate its radius.[15]
After the hydrogen fuel at the core of the main sequence star has been consumed, the star evolves away from the main sequence on the HR diagram. The behavior of a star now depends on its mass, with stars below 0.23 solar masses becoming white dwarfs, while stars with up to 10 solar masses pass through a red giant stage.[16] More massive stars can explode as a Type II supernova.[17]
Stellar parameters
The table below shows typical values for stars along the main sequence. The values of luminosity (L), radius (R) and mass (M) are relative to the Sun—a dwarf star with a spectral classification of G2 V. The actual values for a star may vary by as much as 20–30 percent from the values listed below.[18]
Table of main sequence stellar parameters[19] Stellar
ClassRadius Mass Luminosity Temperature Examples[20] R/R☉ M/M☉ L/L☉ K O5 18 40 500,000 38,000 Zeta Puppis B0 7.4 18 20,000 30,000 Phi1 Orionis B5 3.8 6.5 800 16,400 Pi Andromedae A A0 2.5 3.2 80 10,800 Alpha Coronae Borealis A A5 1.7 2.1 20 8,620 Beta Pictoris F0 1.4 1.7 6 7,240 Gamma Virginis F5 1.2 1.29 2.5 6,540 Eta Arietis G0 1.05 1.10 1.26 6,000 Beta Comae Berenices G2 1.00 1.00 1.00 5,920 Sun[21] G5 0.93 0.93 0.79 5,610 Alpha Mensae K0 0.85 0.78 0.40 5,150 70 Ophiuchi A K5 0.74 0.69 0.16 — 61 Cygni A M0 0.63 0.47 0.063 3,920 Gliese 185[22] M5 0.32 0.21 0.0079 3,120 EZ Aquarii A M8 0.13 0.10 0.0008 — Van Biesbroeck's star[23]
Energy generation
All main sequence stars have a core region where energy is generated by nuclear fusion. The temperature and density of this core are at the levels necessary to sustain the energy production that will support the remainder of the star. A reduction of energy production would cause the overlaying mass to compress the core, resulting in an increase in the fusion rate because of higher temperature and pressure. Likewise an increase in energy production would cause the star to expand, lowering the pressure at the core. Thus the star forms a self-regulating system in hydrostatic equilibrium that is stable over the course of its main sequence lifetime.[24]
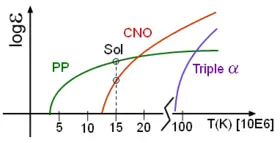
Astronomers divide the main sequence into upper and lower parts, based on the dominant type of fusion process at the core. Stars in the upper main sequence have sufficient mass to use the CNO cycle to fuse hydrogen into helium. This process uses atoms of carbon, nitrogen and oxygen as intermediaries in the fusion process. In the lower main sequence, energy is generated as the result of the proton-proton chain, which directly fuses hydrogen together in a series of stages to produce helium.[25]
At a stellar core temperature of 18 million kelvins, both fusion processes are equally efficient. As this is the core temperature of a star with 1.5 solar masses, the upper main sequence consists of stars above this mass. The apparent upper limit for a main sequence star is 120–200 solar masses.[26] Stars above this mass can not radiate energy fast enough to remain stable, so any additional mass will be ejected in a series of pulsations until the star reaches a stable limit.[27] The lower limit for sustained nuclear fusion is about 0.08 solar masses.[25]
Structure
Because there is a temperature difference between the core and the surface, or photosphere, energy is transported outward. The two modes for transporting this energy are radiation and convection. A radiation zone, where energy is transported by radiation, is stable against convection and there is very little mixing of the plasma. By contrast, in a convection zone the energy is transported by bulk movement of plasma, with hotter material rising and cooler material descending. Convection is a more efficient mode for carrying energy than radiation, but it will only occur under conditions that create a steep temperature gradient.[28][24]
In massive stars (above 10 solar masses)[29] the rate of energy generation by the CNO cycle is very sensitive to temperature, so the fusion is highly concentrated at the core. Consequently, there is a high temperature gradient in the core region, which results in a convection zone for more efficient energy transport.[25] This mixing of material around the core removes the helium ash from the hydrogen burning region, allowing more of the hydrogen in the star to be consumed during the main sequence lifetime. The outer regions of a massive star transport energy by radiation, with little or no convection.[24]
Intermediate mass stars such as Sirius may transport energy primarily by radiation, with a small core convection region.[30] Medium-sized, low mass stars like the Sun have a core region that is stable against convection, with a convection zone near the surface that mixes the outer layers. This results in a steady buildup of a helium-rich core, surrounded by a hydrogen-rich outer region. By contrast, cool, very low-mass stars (below 0.4 solar masses) are convective throughout.[31] Thus, the helium produced at the core is distributed across the star, producing a relatively uniform atmosphere and a proportionately longer main sequence lifespan.[24]
Luminosity-color variation
As non-fusing helium ash accumulates in the core of a main sequence star, the reduction in the abundance of hydrogen per unit mass results in a gradual lowering of the fusion rate within that mass. To compensate, the core temperature and pressure slowly increase, which causes a net increase in the overall fusion rate (to support the greater density of the inner star). This produces a steady increase in the luminosity and radius of the star over time.[11] Thus, for example, the luminosity of the early Sun was only about 70 percent of its current value.[32] As a star ages this luminosity increase changes its position on the HR diagram. This effect results in a broadening of the main sequence band because stars are observed at random stages in their lifetime.[33]
Other factors that broaden the main sequence band on the HR diagram include uncertainty in the distance to stars and the presence of unresolved binary stars that can alter the observed stellar parameters. However, even perfect observation would show a fuzzy main sequence because mass is not the only parameter that affects a star's color and luminosity. In addition to variations in chemical composition—both because of the initial abundances and the star's evolutionary status,[34] interaction with a close companion,[35] rapid rotation,[36] or a magnetic field can also change a main sequence star's position slightly on the HR diagram, to name just a few factors. As an example, there are stars that have a very low abundance of elements with higher atomic numbers than helium—known as metal-poor stars—that lie just below the main sequence. Known as subdwarfs, these stars are also fusing hydrogen in their core and so they mark the lower edge of the main sequence's fuzziness resulting from chemical composition.[37]
A nearly vertical region of the HR diagram, known as the instability strip, is occupied by pulsating variable stars. These stars vary in magnitude at regular intervals, giving them a pulsating appearance. The strip intersects the upper part of the main sequence in the region of class A and F stars, which are between one and two solar masses. Main sequence stars in this region experience only small changes in magnitude and so this variation is difficult to detect.[38]
Lifetime
The total amount of energy that a star can generate through nuclear fusion of hydrogen is limited by the amount of hydrogen fuel that can be consumed at the core. For a star in equilibrium, the energy generated at the core must be at least equal to the energy radiated at the surface. Since the luminosity gives the amount of energy radiated per unit time, the total life span can be estimated, to first approximation, as the total energy produced divided by the star's luminosity.[39]
For a star with at least 0.5 solar masses, once the hydrogen supply in its core is exhausted and it expands to become a red giant, it can start to fuse helium atoms to form carbon. As the energy output of the helium fusion process per unit mass is only about a tenth the energy output of the hydrogen process, this stage will only last for about 10 percent of a star's total active lifetime. Thus, about 90 percent of the observed stars above 0.5 solar masses will be on the main sequence.[40]
On average, main sequence stars are known to follow an empirical mass-luminosity relationship.[41] The luminosity (L) of the star is roughly proportional to the total mass (M) as the following power law:
The amount of fuel available for nuclear fusion is proportional to the mass of the star. Thus, the lifetime of a star on the main sequence can be estimated by comparing it to solar evolutionary models. The Sun has been a main sequence star for about 4.5 billion years and it will become a red giant in 6.5 billion years,[42] for a total main sequence lifetime of roughly 1010 years. Hence:[39][43]
where M and L are the mass and luminosity of the star, respectively, is a solar mass, is the solar luminosity and is the star's estimated main sequence lifetime.
This is a counter-intuitive result, as more massive stars have more fuel to burn and might be expected to last longer. Instead, the most massive stars may remain on the main sequence for only a few million years, while stars with less than a tenth of a solar mass may last for over a trillion years.[44] For massive stars, however, this mass-luminosity relationship poorly matches the estimated lifetime. A more accurate representation gives a different function for various ranges of mass.
The exact mass-luminosity relationship depends on how efficiently energy can be transported from the core to the surface. A higher opacity has an insulating effect that retains more energy at the core, so the star does not need to produce as much energy to remain in hydrostatic equilibrium. By contrast, a lower opacity means energy escapes more rapidly and the star must burn more fuel to remain in equilibrium.[45] Note, however, that a sufficiently high opacity can result in energy transport via convection, which changes the conditions needed to remain in equilibrium.[11]
In high mass main sequence stars, the opacity is dominated by electron scattering, which is nearly constant with increasing temperature. Thus the luminosity only increases as the cube of the star's mass.[46] For stars below 10 times the solar mass, the opacity becomes dependent on temperature, resulting in the luminosity varying approximately as the fourth power of the star's mass.[47] For very low mass stars, molecules in the atmosphere also contribute to the opacity. Below about 0.5 solar masses, the luminosity of the star varies as the mass to the power of 2.3, producing a flattening of the slope on a graph of mass versus luminosity. Even these refinements are only an approximation, however, and the mass-luminosity relation can vary depending on a star's composition.[48]
Evolutionary tracks
Once a main sequence star consumes the hydrogen at its core, the loss of energy generation causes gravitational collapse to resume. For stars with less than 0.23 solar masses,[16] energy generation by nuclear fusion comes to a halt and it becomes a white dwarf. (The star now migrates to the lower left on the HR diagram.) For higher mass stars with up to 10 solar masses, the hydrogen surrounding the helium core reaches sufficient temperature and pressure to undergo fusion, forming a hydrogen-burning shell. In consequence of this change, the outer envelope of the star expands and decreases in temperature, turning it into a red giant. At this point the star is evolving off the main sequence and entering the giant branch. The path the star now follows across the HR diagram is called an evolutionary track.
The helium core of a red giant continues to collapse until it is entirely supported by electron degeneracy pressure—a quantum mechanical effect that restricts how closely matter can be compacted. For stars of more than about 0.5 solar masses,[49] the core can reach a temperature where it becomes hot enough to burn helium into carbon via the triple alpha process.[50][51] Stars with at least four solar masses can also fuse elements with higher atomic numbers. For stars with ten solar masses, this process can lead to a cataclysmic explosion as a Type II supernova.[17]
When a cluster of stars is formed at about the same time, the life span of these stars will depend on their individual masses. The most massive stars will leave the main sequence first, followed steadily in sequence by stars of ever lower masses. Thus the stars will evolve in order of their position on the main sequence, proceeding from the most massive at the left toward the right of the HR diagram. The current position where stars in this cluster are leaving the main sequence is known as the turn-off point. By knowing the main sequence lifespan of stars at this point, it becomes possible to estimate the age of the cluster.[52]
See also
Notes
- ↑ Malcolm S. Longair, The Cosmic Century: A History of Astrophysics and Cosmology (Cambridge, UK: Cambridge University Press, 2004, ISBN 0521474361).
- ↑ 2.0 2.1 Laurie M. Brown, Abraham Pais, and A.B. Pippard, Twentieth Century Physics (Boca Raton, FL: CRC Press, 1995, ISBN 0750303107).
- ↑ 3.0 3.1 H.N. Russell, "Giant" and "dwarf" stars, The Observatory 36: 324–329. Retrieved December 14, 2008.
- ↑ Bengt Strömgren, On the Interpretation of the Hertzsprung-Russell-Diagram, Zeitschrift für Astrophysik. 7: 222–248. Retrieved December 14, 2008.
- ↑ Evry L. Schatzman and Francoise Praderie, The Stars (Berlin, DE: Springer, 1993, ISBN 3540541969).
- ↑ W.N. Morgan, P.C. Keenan, and E. Kellman, An atlas of stellar spectra, with an outline of spectral classification, The University of Chicago press. Retrieved December 14, 2008.
- ↑ 7.0 7.1 7.2 Albrecht Unsöld, The New Cosmos (New York, NY: Springer-Verlag, 1969), 268.
- ↑ George Gloeckler and Johannes Geisso, Composition of the local interstellar medium as diagnosed with pickup ions, Advances in Space Research 34 (1): 53–60. Retrieved December 14, 2008.
- ↑ Govert Schilling, New Model Shows Sun Was a Hot Young Star, Science 293 (5538): 2188–2189. Retrieved December 14, 2008.
- ↑ SAO Encyclopedia of Astronomy, Zero Age Main Sequence, Swinburne University. Retrieved December 14, 2008.
- ↑ 11.0 11.1 11.2 Donald D. Clayton, Principles of Stellar Evolution and Nucleosynthesis (Chicago, IL: University of Chicago Press, 1983, ISBN 0226109534).
- ↑ Australia Telescope Outreach and Education, Main Sequence Stars. Retrieved December 14, 2008.
- ↑ Moore, Patrick. 2006. The Amateur Astronomer (Berlin, DE; New York, NY: Springer, ISBN 1852338784).
- ↑ SAO Encyclopedia of Astronomy, White Dwarf, Swinburne University. Retrieved December 14, 2008.
- ↑ University of Nebraska, Origin of the Hertzsprung-Russell Diagram. Retrieved December 14, 2008.
- ↑ 16.0 16.1 Fred C. Adams and Gregory Laughlin, A Dying Universe: The Long Term Fate and Evolution of Astrophysical Objects, Reviews of Modern Physics 69 (2): 337–372.
- ↑ 17.0 17.1 Gerry Gilmore, The Short Spectacular Life of a Superstar, Science 304 (5697): 1915–1916.
- ↑ Lionel Siess, Computation of Isochrones, Institut d'Astronomie et d'Astrophysique, Université libre de Bruxelles. Retrieved December 14, 2008.
- ↑ Martin V. Zombeck, Handbook of Space Astronomy and Astrophysics, 2nd edition (Cambridge, UK: Cambridge University Press, ISBN 0521347874). Retrieved December 14, 2008.
- ↑ Centre de Données astronomiques de Strasbourg, SIMBAD Astronomical Database. Retrieved December 14, 2008.
- ↑ The Sun is a typical type G2V star.
- ↑ Centre de Données astronomiques de Strasbourg, LTT 2151—High proper-motion Star. Retrieved December 14, 2008.
- ↑ RECONS, List of the Nearest Hundred Nearest Star Systems, Research Consortium on Nearby Stars. Retrieved December 14, 2008.
- ↑ 24.0 24.1 24.2 24.3 Jerome James Brainerd, Main-Sequence Stars, The Astrophysics Spectator.
- ↑ 25.0 25.1 25.2 Hannu Karttunen, Fundamental Astronomy (Berlin, DE: Springer, 2003, ISBN 3540001794).
- ↑ M.S. Oey and C.J. Clarke, Statistical Confirmation of a Stellar Upper Mass Limit, The Astrophysical Journal 620 (1): L43–L46. Retrieved December 14, 2008.
- ↑ Kenneth Ziebarth, On the Upper Mass Limit for Main-Sequence Stars, Astrophysical Journal. 162 (1970): 947–962. Retrieved December 14, 2008.
- ↑ Lawrence H. Aller, Atoms, Stars, and Nebulae (Cambridge, UK: Cambridge University Press, ISBN 0521310407).
- ↑ A.G. Bressan, C. Chiosi, and G. Bertelli, Mass loss and overshooting in massive stars, Astronomy and Astrophysics 102 (1): 25–30. Retrieved December 14, 2008.
- ↑ Jim Lochner, Meredith Gibb, and Phil Newman, Stars, NASA. Retrieved December 14, 2008.
- ↑ Pavel Kroupa, The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems. Science 295 (5552): 82–91.
- ↑ D.O. Gough, Solar interior structure and luminosity variations, Solar Physics 74: 21–34. Retrieved December 14, 2008.
- ↑ Thanu Padmanabhan, Theoretical Astrophysics (Cambridge University Press, ISBN 0521562414).
- ↑ J.T. Wright, Do We Know of Any Maunder Minimum Stars? The Astronomical Journal 128 (3): 1273–1278. Retrieved December 14, 2008.
- ↑ Roger John Tayler, The Stars: Their Structure and Evolution (Cambridge, UK: Cambridge University Press, 1994, ISBN 0521458854).
- ↑ I.P.A. Sweet and A.E. Roy, The structure of rotating stars, Monthly Notices of the Royal Astronomical Society 113: 701–715. Retrieved December 14, 2008.
- ↑ Adam J. Burgasser, J. Davy Kirkpatrick, and Sebastien Lepine, Spitzer Studies of Ultracool Subdwarfs: Metal-poor Late-type M, L and T Dwarfs, in F. Favata, Proceedings of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun (Dordrecht, NL: D. Reidel Publishing Co., 2005, ISBN 9789290928713), 237. Retrieved December 14, 2008.
- ↑ S.F. Green, Mark Henry Jones, and S. Jocelyn Burnell, An Introduction to the Sun and Stars (Cambridge, UK: Cambridge University Press, 2004, ISBN 0521546222).
- ↑ 39.0 39.1 Michael W. Richmond, Stellar evolution on the main sequence, Rochester Institute of Technology. Retrieved December 14, 2008.
- ↑ David Arnett, Supernovae and Nucleosynthesis: An Investigation of the History of Matter, from the Big Bang to the Present (Princeton, NJ: Princeton University Press, 1996, ISBN 0691011478).
- ↑ Stefano Lecchini, How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation (St. Louis, MO: Bern Studies in the History and Philosophy of Science, 2007, ISBN 3952288268).
- ↑ I. Juliana Sackmann, Arnold I. Boothroyd, and Kathleen E. Kraemer, Our Sun. III. Present and Future, Astrophysical Journal 418 (1993): 457–468. Retrieved December 14, 2008.
- ↑ Cosmos, Main Sequence Lifetime. Swinburne University of Technology. Retrieved December 14, 2008.
- ↑ Gregory Laughlin, Peter Bodenheimer, and Fred C. Adams, The End of the Main Sequence, The Astrophysical Journal 482 (1997): 420–432.
- ↑ James N. Imamura, Mass-Luminosity Relationship, University of Oregon.
- ↑ Dina Prialnik, An Introduction to the Theory of Stellar Structure and Evolution (Cambridge, UK: Cambridge University Press, 2000, ISBN 052165937X).
- ↑ Rolfs, Claus E., and William S. Rodney, Cauldrons in the Cosmos: Nuclear Astrophysics (Chicago, IL: University of Chicago Press, 1988, ISBN 0226724573).
- ↑ Pavel Kroupa, The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems, Science 295 (5552): 82–91.
- ↑ Hans O.U. Fynbo, et al., Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances, Nature 433 (2004): 136–139.
- ↑ Michael L. Sitko, Stellar Structure and Evolution, University of Cincinnati. Retrieved December 14, 2008.
- ↑ Australia Telescope Outreach and Education, Post-Main Sequence Stars. Retrieved December 14, 2008.
- ↑ Lawrence M. Krauss and Brian Chaboyer, Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology, Science 299 (5603): 65–69.
ReferencesISBN links support NWE through referral fees
- Aller, Lawrence H. 1991. Atoms, Stars, and Nebulae. Cambridge, UK: Cambridge University Press. ISBN 0521310407.
- Arnett, David. 1996. Supernovae and Nucleosynthesis: An Investigation of the History of Matter, from the Big Bang to the Present. Princeton, NJ: Princeton University Press. ISBN 0691011478.
- Brown, Laurie M., Abraham Pais, and A.B. Pippard. 1995. Twentieth Century Physics. Boca Raton, FL: CRC Press. ISBN 0750303107.
- Clayton, Donald D. 1983. Principles of Stellar Evolution and Nucleosynthesis. Chicago, IL: University of Chicago Press. ISBN 0226109534.
- Green, S.F., Mark Henry Jones, and S. Jocelyn Burnell. 2004. An Introduction to the Sun and Stars. Cambridge, UK: Cambridge University Press. ISBN 0521546222.
- Karttunen, Hannu. 2003. Fundamental Astronomy. New York, NY: Springer. ISBN 3540001794.
- Lecchini, Stefano. 2007. How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation. St. Louis, MO: Bern Studies in the History and Philosophy of Science. ISBN 3952288268.
- Longair, Malcolm S. 2006. The Cosmic Century: A History of Astrophysics and Cosmology. Cambridge, UK: Cambridge University Press. ISBN 0521474361.
- Moore, Patrick. 2006. The Amateur Astronomer. Berlin, DE: Springer. ISBN 1852338784.
- Padmanabhan, Thanu. 2001. Theoretical Astrophysics. Cambridge University Press. ISBN 0521562414.
- Prialnik, Dina. 2000. An Introduction to the Theory of Stellar Structure and Evolution. Cambridge, UK: Cambridge University Press. ISBN 052165937X.
- Rolfs, Claus E., and William S. Rodney. 1988. Cauldrons in the Cosmos: Nuclear Astrophysics. Chicago, IL: University of Chicago Press. ISBN 0226724573.
- Schatzman, Evry L., and Francoise Praderie. 1993. The Stars. Berlin, DE; New York, NY: Springer. ISBN 3540541969.
- Tayler, Roger John. 1994. The Stars: Their Structure and Evolution. Cambridge, UK: Cambridge University Press. ISBN 0521458854.
- Zombeck, Martin V. 1990. Handbook of Space Astronomy and Astrophysics, 2nd edition. Cambridge, UK: Cambridge University Press. ISBN 0521347874.
External links
All links retrieved March 27, 2025.
- Charity, Mitchell. 2001. What color are the stars?. Vendian Systems.
| |||||||||||||||||
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.



![{\displaystyle {\begin{smallmatrix}\tau _{ms}\ \approx \ 10^{10}{\text{years}}\cdot \left[{\frac {M}{M_{\bigodot }}}\right]\cdot \left[{\frac {L_{\bigodot }}{L}}\right]\ =\ 10^{10}{\text{years}}\cdot \left[{\frac {M_{\bigodot }}{M}}\right]^{2.5}\end{smallmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/096c601edb6544f3b9914e37d7875fdaa4705888)



