Black body

Black-body radiation curves at different temperatures: 3000 K, 4000 K, and 5000 K. As the temperature decreases, the peak of the black-body radiation curve moves to lower intensities and longer wavelengths. The black-body radiation graph is also compared with the classical model of Rayleigh and Jeans.

In physics, a black body (in an ideal sense) is an object that absorbs all electromagnetic radiation that falls on it, without any of the radiation passing through it or being reflected by it. Because it does not reflect or transmit visible light, the object appears black when it is cold.

When heated, the black body becomes an ideal source of thermal radiation, which is called black-body radiation. If a perfect black body at a certain temperature is surrounded by other objects in equilibrium at the same temperature, it will on average emit exactly as much as it absorbs, at the same wavelengths and intensities of radiation that it had absorbed.

The temperature of the object is directly related to the wavelengths of the light it emits. At room temperature, black bodies emit infrared light, but as the temperature increases past a few hundred degrees Celsius, black bodies start to emit at visible wavelengths, from red through orange, yellow, and white before ending up at blue, beyond which the emission includes increasing amounts of ultraviolet radiation.

The color (chromaticity) of black-body radiation depends on the temperature of the black body. The locus of such colors (shown here in CIE 1931 x,y space) is known as the Planckian locus.

Black bodies have been used to test the properties of thermal equilibrium because they emit radiation that is distributed thermally. In classical physics, each different Fourier mode in thermal equilibrium should have the same energy, leading to the theory of ultraviolet catastrophe that there would be an infinite amount of energy in any continuous field. Studies of black-body radiation led to the revolutionary field of quantum mechanics. In addition, black-body laws have been used to determine the black-body temperatures of planets.

Overview

If a small window is opened into an oven, any light that enters the window has a very low probability of leaving without being absorbed. Conversely, the hole acts as a nearly ideal black-body radiator. This makes peepholes into furnaces good sources of blackbody radiation, and some people call it cavity radiation for this reason.

In the laboratory, black-body radiation is approximated by the radiation from a small hole entrance to a large cavity, a hohlraum. Any light entering the hole would have to reflect off the walls of the cavity multiple times before it escaped, in which process it is nearly certain to be absorbed. This occurs regardless of the wavelength of the radiation entering (as long as it is small compared to the hole). The hole, then, is a close approximation of a theoretical black body and, if the cavity is heated, the spectrum of the hole's radiation (i.e., the amount of light emitted from the hole at each wavelength) will be continuous, and will not depend on the material in the cavity (compare with emission spectrum). By a theorem proved by Gustav Kirchhoff, this curve depends only on the temperature of the cavity walls. Kirchhoff introduced the term "black body" in 1860.

Calculating this curve was a major challenge in theoretical physics during the late nineteenth century. The problem was finally solved in 1901 by Max Planck as Planck's law of black-body radiation. By making changes to Wien's Radiation Law (not to be confused with Wien's displacement law) consistent with thermodynamics and electromagnetism, he found a mathematical formula fitting the experimental data in a satisfactory way. To find a physical interpretation for this formula, Planck had then to assume that the energy of the oscillators in the cavity was quantized (i.e., integer multiples of some quantity). Einstein built on this idea and proposed the quantization of electromagnetic radiation itself in 1905 to explain the photoelectric effect.

These theoretical advances eventually resulted in the superseding of classical electromagnetism by quantum electrodynamics. Today, these quanta are called photons and the black-body cavity may be thought of as containing a gas of photons. In addition, it led to the development of quantum probability distributions, called Fermi-Dirac statistics and Bose-Einstein statistics, each applicable to a different class of particle, which are used in quantum mechanics instead of the classical distributions.

The temperature of a Pāhoehoe lava flow can be estimated by observing its color. The result agrees well with the measured temperatures of lava flows at about 1,000 to 1,200 °C.

The wavelength at which the radiation is strongest is given by Wien's displacement law, and the overall power emitted per unit area is given by the Stefan-Boltzmann law. So, as temperature increases, the glow color changes from red to yellow to white to blue. Even as the peak wavelength moves into the ultra-violet, enough radiation continues to be emitted in the blue wavelengths that the body will continue to appear blue. It will never become invisible — indeed, the radiation of visible light increases monotonically with temperature.

The radiance or observed intensity is not a function of direction. Therefore a black body is a perfect Lambertian radiator.

Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be. The emissivity of a material specifies how well a real body radiates energy as compared with a black body. This emissivity depends on factors such as temperature, emission angle, and wavelength. However, it is typical in engineering to assume that a surface's spectral emissivity and absorptivity do not depend on wavelength, so that the emissivity is a constant. This is known as the grey body assumption.

Although Planck's formula predicts that a black body will radiate energy at all frequencies, the formula is only applicable when many photons are being measured. For example, a black body at room temperature (300 K) with one square meter of surface area will emit a photon in the visible range once every thousand years or so, meaning that for most practical purposes, the black body does not emit in the visible range.

When dealing with non-black surfaces, the deviations from ideal black-body behavior are determined by both the geometrical structure and the chemical composition, and follow Kirchhoff's Law: emissivity equals absorptivity, so that an object that does not absorb all incident light will also emit less radiation than an ideal black body.

WMAP image of the cosmic microwave background radiation anisotropy. It has the most precise thermal emission spectrum known and corresponds to a temperature of 2.725 kelvin (K) with an emission peak at 160.2 GHz.

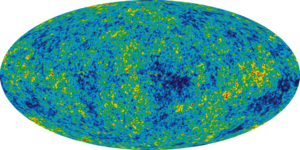
In astronomy, objects such as stars are frequently regarded as black bodies, though this is often a poor approximation. An almost perfect black-body spectrum is exhibited by the cosmic microwave background radiation. Hawking radiation is black-body radiation emitted by black holes.

Black body simulators

Although a black body is a theoretical object, (i.e. emissivity (e) = 1.0), common applications define a source of infrared radiation as a black body when the object approaches an emissivity of 1.0, (typically e = .99 or better). A source of infrared radiation less than .99 is referred to as a greybody. Applications for black body simulators typically include the testing and calibration of infrared systems and infrared sensor equipment.

Radiation emitted by a human body

Much of a person's energy is radiated away in the form of infrared energy. Some materials are transparent to infrared light, while opaque to visible light (note the plastic bag). Other materials are transparent to visible light, while opaque or reflective to the infrared (note the man's glasses).

Black-body laws can be applied to human beings. For example, some of a person's energy is radiated away in the form of electromagnetic radiation, most of which is infrared.

The net power radiated is the difference between the power emitted and the power absorbed:

$P_{net}=P_{emit}-P_{absorb}.$

Applying the Stefan–Boltzmann law,

$P_{net}=A\sigma \epsilon \left(T^{4}-T_{0}^{4}\right)\,$.

The total surface area of an adult is about 2 m², and the mid- and far-infrared emissivity of skin and most clothing is near unity, as it is for most nonmetallic surfaces. Skin temperature is about 33°C, but clothing reduces the surface temperature to about 28°C when the ambient temperature is 20°C. Hence, the net radiative heat loss is about

$P_{net}=100\ \mathrm {W} \,$.

The total energy radiated in one day is about 9 MJ (Mega joules), or 2000 kcal (food calories). Basal metabolic rate for a 40-year-old male is about 35 kcal/(m²•h), which is equivalent to 1700 kcal per day assuming the same 2 m² area. However, the mean metabolic rate of sedentary adults is about 50 percent to 70 percent greater than their basal rate.

There are other important thermal loss mechanisms, including convection and evaporation. Conduction is negligible since the Nusselt number is much greater than unity. Evaporation (perspiration) is only required if radiation and convection are insufficient to maintain a steady state temperature. Free convection rates are comparable, albeit somewhat lower, than radiative rates. Thus, radiation accounts for about 2/3 of thermal energy loss in cool, still air. Given the approximate nature of many of the assumptions, this can only be taken as a crude estimate. Ambient air motion, causing forced convection, or evaporation reduces the relative importance of radiation as a thermal loss mechanism.

Also, applying Wien's Law to humans, one finds that the peak wavelength of light emitted by a person is

$\lambda _{peak}={\frac {2.898\times 10^{6}\ \mathrm {K} \cdot \mathrm {nm} }{305\ \mathrm {K} }}=9500\ \mathrm {nm} \,$.

This is why thermal imaging devices designed for human subjects are most sensitive to 7–14 micrometers wavelength.

Equations governing black bodies

Planck's law of black-body radiation

$I(\nu ,T)d\nu ={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{kT}}-1}}\,d\nu$

where

• $I(\nu ,T)d\nu \,$ is the amount of energy per unit surface area per unit time per unit solid angle emitted in the frequency range between ν and ν+dν by a black body at temperature T;
• $h\,$ is Planck's constant;
• $c\,$ is the speed of light; and
• $k\,$ is Boltzmann's constant.

Wien's displacement law

The relationship between the temperature T of a black body, and wavelength $\lambda _{max}$ at which the intensity of the radiation it produces is at a maximum is

• $T\lambda _{\mathrm {max} }=2.898...\times 10^{6}\ \mathrm {nm\ K} .\,$

The nanometer is a convenient unit of measure for optical wavelengths. Note that 1 nanometer is equivalent to 10⁻⁹ meters.

Stefan–Boltzmann law

The total energy radiated per unit area per unit time $j^{\star }$ (in watts per square meter) by a black body is related to its temperature T (in kelvins) and the Stefan–Boltzmann constant $\sigma$ as follows:

$j^{\star }=\sigma T^{4}.\,$

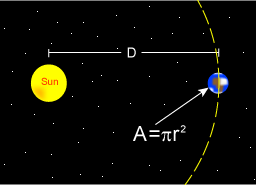
Temperature relation between a planet and its star

Here is an application of black-body laws to determine the black body temperature of a planet. The surface may be warmer due to the greenhouse effect.

Factors

Earth's longwave thermal radiation intensity, from clouds, atmosphere and ground

The temperature of a planet depends on a few factors:

• Incident radiation (from the Sun, for example)
• Emitted radiation (for example [[Earth's_energy_budget#Outgoing_energy|Earth's infrared glow]])
• The albedo effect (the fraction of light a planet reflects)
• The greenhouse effect (for planets with an atmosphere)
• Energy generated internally by a planet itself (due to Radioactive decay, tidal heating and adiabatic contraction due to cooling).

For the inner planets, incident and emitted radiation have the most significant impact on temperature. This derivation is concerned mainly with that.

Assumptions

If we assume the following:

1. The Sun and the Earth both radiate as spherical black bodies.
2. The Earth is in thermal equilibrium.

then we can derive a formula for the relationship between the Earth's temperature and the Sun's surface temperature.

Derivation

To begin, we use the Stefan–Boltzmann law to find the total power (energy/second) the Sun is emitting:

The Earth only has an absorbing area equal to a two dimensional circle, rather than the surface of a sphere.

$P_{Semt}=\left(\sigma T_{S}^{4}\right)\left(4\pi R_{S}^{2}\right)\qquad \qquad (1)$

where

$\sigma \,$ is the Stefan–Boltzmann constant,

$T_{S}\,$ is the surface temperature of the Sun, and

$R_{S}\,$ is the radius of the Sun.

The Sun emits that power equally in all directions. Because of this, the Earth is hit with only a tiny fraction of it. This is the power from the Sun that the Earth absorbs:

$P_{Eabs}=P_{Semt}(1-\alpha )\left({\frac {\pi R_{E}^{2}}{4\pi D^{2}}}\right)\qquad \qquad (2)$

where

$R_{E}\,$ is the radius of the Earth and

$D\,$ is the distance between the Sun and the Earth.

$\alpha \$ is the albedo of Earth.

Even though the earth only absorbs as a circular area $\pi R^{2}$, it emits equally in all directions as a sphere:

$P_{Eemt}=\left(\sigma T_{E}^{4}\right)\left(4\pi R_{E}^{2}\right)\qquad \qquad (3)$

where $T_{E}$ is the black body temperature of the earth.

Now, our second assumption was that the earth is in thermal equilibrium, so the power absorbed must equal the power emitted:

$P_{Eabs}=P_{Eemt}\,$

So plug in equations 1, 2, and 3 into this and we get

$\left(\sigma T_{S}^{4}\right)\left(4\pi R_{S}^{2}\right)(1-\alpha )\left({\frac {\pi R_{E}^{2}}{4\pi D^{2}}}\right)=\left(\sigma T_{E}^{4}\right)\left(4\pi R_{E}^{2}\right).\,$

Many factors cancel from both sides and this equation can be greatly simplified.

The result

After canceling of factors, the final result is

$T_{S}{\sqrt {\frac {{\sqrt {1-\alpha }}R_{S}}{2D}}}=T_{E}$

where

$T_{S}\,$ is the surface temperature of the Sun,

$R_{S}\,$ is the radius of the Sun,

$D\,$ is the distance between the Sun and the Earth,

$\alpha$ is the albedo of the Earth, and

$T_{E}\,$ is the blackbody temperature of the Earth.

In other words, given the assumptions made, the temperature of Earth depends only on the surface temperature of the Sun, the radius of the Sun, the distance between Earth and the Sun and the albedo of Earth.

Temperature of Earth

If we substitute in the measured values for the Sun,

$T_{S}=5778\ \mathrm {K} ,$

$R_{S}=6.96\times 10^{8}\ \mathrm {m} ,$

$D=1.5\times 10^{11}\ \mathrm {m} ,$

$\alpha =0.3\$

we'll find the effective temperature of the Earth to be

$T_{E}=255\ \mathrm {K} .$

This is the black body temperature as measured from space, while the surface temperature is higher due to the greenhouse effect

Doppler effect for a moving blackbody

The Doppler effect is the well known phenomenon describing how observed frequencies of light are "shifted" when a light source is moving relative to the observer. If f is the emitted frequency of a monochromatic light source, it will appear to have frequency f' if it is moving relative to the observer :

$f'=f{\frac {1}{\sqrt {1-v^{2}/c^{2}}}}(1-{\frac {v}{c}}\cos \theta )$

where v is the velocity of the source in the observer's rest frame, θ is the angle between the velocity vector and the observer-source direction, and c is the speed of light. This is the fully relativistic formula, and can be simplified for the special cases of objects moving directly towards ( θ = π) or away ( θ = 0) from the observer, and for speeds much less than c.

To calculate the spectrum of a moving blackbody, then, it seems straightforward to simply apply this formula to each frequency of the blackbody spectrum. However, simply scaling each frequency like this is not enough. We also have to account for the finite size of the viewing aperture, because the solid angle receiving the light also undergoes a Lorentz transformation. (We can subsequently allow the aperture to be arbitrarily small, and the source arbitrarily far, but this cannot be ignored at the outset.) When this effect is included, it is found that a blackbody at temperature T that is receding with velocity v appears to have a spectrum identical to a stationary blackbody at temperature T', given by:

$T'=T{\frac {1}{\sqrt {1-v^{2}/c^{2}}}}(1-{\frac {v}{c}}\cos \theta )$

For the case of a source moving directly towards or away from the observer, this reduces to

$T'=T{\sqrt {\frac {c-v}{c+v}}}$

Here v > 0 indicates a receding source, and v < 0 indicates an approaching source.

This is an important effect in astronomy, where the velocities of stars and galaxies can reach significant fractions of c. An example is found in the cosmic microwave background radiation, which exhibits a dipole anisotropy from the Earth's motion relative to this blackbody radiation field.

See also

• Color
• Electromagnetic radiation
• Light
• Photon
• Temperature
• Thermometer
• Ultraviolet

References

ISBN links support NWE through referral fees

• Cole, George H.A., Michael M. Woolfson. Planetary Science: The Science of Planets Around Stars. Bristol, UK: Institute of Physics Publishing, 2002. ISBN 075030815X
• Gill, T. P. The Doppler Effect. London, UK: Logos Press, 1965.
• Harris, J. and F. Benedict. A Biometric Study of Human Basal Metabolism. Proc Natl Acad Sci USA 4(12) (1918): 370–373.
• Huang, Kerson. Statistical Mechanics. New York, NY: John Wiley & Sons, 1967.
• Kroemer, Herbert, and Charles Kittel. Thermal Physics, 2nd ed. W. H. Freeman Company, 1980. ISBN 0716710889
• Landau, L. D., and E. M. Lifshitz. Statistical Physics, 3rd Edition, Part 1. Oxford, UK: Butterworth-Heinemann, 1996 (original 1958).
• Tipler, Paul, and Ralph Llewellyn. Modern Physics, 4th ed. W. H. Freeman, 2002. ISBN 0716743450

External links

All links retrieved October 31, 2023.

• Calculating Blackbody Radiation Interactive calculator with Doppler Effect. Includes most systems of units.
• Cooling Mechanisms for Human Body - From Hyperphysics.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Black body  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Black body"

Note: Some restrictions may apply to use of individual images which are separately licensed.