Cosmic microwave background radiation

From New World Encyclopedia
Previous (Cosmetics)
Next (Cosmic ray)


Physical cosmology
WMAP 2008.png
Universe · Big Bang
Age of the Universe
Timeline of the Big Bang
Ultimate fate of the universe

In cosmology, the cosmic microwave background radiation CMB (also CMBR, CBR, MBR, and relic radiation) is a form of electromagnetic radiation filling the universe. In simple terms, when looking at the sky with a radio telescope, the space between the stars and galaxies is not black. Instead there is a very faint glow, almost exactly the same in all directions, not coming from any star or galaxy. This glow is strongest in the microwave region of the radio spectrum, hence the name cosmic microwave background radiation. The name relic radiation comes from the leading theory to explain this radiation, which holds it is left over from the early universe. Precise measurements of cosmic background radiation are critical to cosmology, since any proposed model of the universe must explain this radiation as we observe it.

The CMBR is well explained by the Big Bang theory - when the universe was young, before stars and planets, it was smaller and much hotter, and filled with a uniform glow from its red-hot fog of hydrogen plasma. As the universe expanded it grew cooler - both the plasma itself and the radiation filling it. When the universe got cool enough, stable atoms could form. These atoms could no longer absorb the thermal radiation, and the universe became transparent instead of a fog. The photons that were around at that time have been cruising around ever since, though growing fainter and cooler since the exact same photons fill a larger and larger universe.

Features

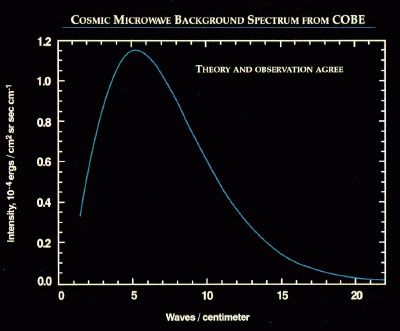
The cosmic microwave background spectrum measured by the FIRAS instrument on the COBE satellite is the most precisely measured black body spectrum in nature. The data points and error bars on this graph are obscured by the theoretical curve.

Technically, the CMBR has a thermal black body spectrum at a temperature of 2.725 K, thus the spectrum peaks in the microwave range frequency of 160.2 GHz, corresponding to a 1.9mm wavelength. The CMB's discovery in 1964 by astronomers Arno Penzias and Robert Wilson[1] was the culmination of work initiated in the 1940s.[2]

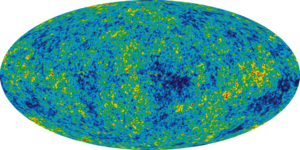
Crucially, the glow is almost but not quite uniform in all directions, and shows a very specific pattern equal to that expected if the inherent randomness of a red-hot gas is blown up to the size of the universe. In particular, the spatial power spectrum (how much difference is observed versus how far apart the regions are on the sky) contains small anisotropies, or irregularities, which vary with the size of the region examined. They have been measured in detail, and match to within experimental error what would be expected if small thermal fluctuations had expanded to the size of the observable space we can detect today. Although many different processes might produce the general form of a black body spectrum, no model other than the Big Bang has yet explained these fluctuations. As a result, most cosmologists consider this radiation to be the best evidence for the Big Bang model of the universe.

The cosmic microwave background is isotropic to roughly one part in 100,000: the root mean square variations are only 18 µK.[3] The Far-Infrared Absolute Spectrophotometer(FIRAS) instrument on the NASA Cosmic Background Explorer (COBE) satellite has carefully measured the spectrum of the cosmic microwave background. FIRAS compared the CMB with an internal reference black body and the spectra agreed to within the experimental error. They concluded that any deviations from the black body form that might still remain undetected in the CMB spectrum over the wavelength range from 0.5 to 5 mm must have a weighted rms value of at most 50 parts per million (0.005 percent) of the CMB peak brightness.[4] This made the CMB spectrum the most precisely measured black body spectrum in nature.

The cosmic microwave background, and its level of isotropy, are both predictions of Big Bang theory. In the theory, the early universe was made up of a hot plasma of photons, electrons and baryons. The photons were constantly interacting with the plasma through Thomson scattering. As the universe expanded, adiabatic cooling caused the plasma to cool until it became favorable for electrons to combine with protons and form hydrogen atoms. This happened at around 3,000°K or when the universe was approximately 379,000 years old (z=1088). At this point, the photons scattered off the now neutral atoms and began to travel freely through space. This process is called recombination or decoupling (referring to electrons combining with nuclei and to the decoupling of matter and radiation respectively).

The color temperature of the photons has continued to diminish ever since; now down to 2.725°K, their temperature will continue to drop as the universe expands. Accordingly, the radiation from the sky we measure today comes (according to the Big Bang theory) from a spherical surface called the surface of last scattering. This represents the collection of points in space (currently around 46 billion light-years from the Earth—see observable universe) at which the decoupling event is believed to have occurred, and at a point in time (less than 400,000 years after the Big Bang, or about 13.7 billion years ago) such that the photons from that distance have just reached observers.

The Big Bang theory suggests that the cosmic microwave background fills all of observable space, and that most of the radiation energy in the universe is in the cosmic microwave background, which makes up a fraction of roughly 5×10-5 of the total density of the universe.[5]

Two of the greatest successes of the big bang theory are its prediction of its almost perfect black body spectrum and its detailed prediction of the anisotropies in the cosmic microwave background. The recent Wilkinson Microwave Anisotropy Probe has precisely measured these anisotropies over the whole sky down to angular scales of 0.2 degrees.[6] These can be used to estimate the parameters of the standard Lambda-CDM model of the big bang. Some information, such as the shape of the Universe, can be obtained straightforwardly from the cosmic microwave background, while others, such as the Hubble constant, are not constrained and must be inferred from other measurements.[7]

History

Timeline of the CMB
Important people and dates
1941 Andrew McKellar The observational detection of an average bolometric temperature of 2.3 K based on the study of interstellar absorption lines is reported from the Dominion Astrophysical Observatory.[8][9]
1946 Robert Dicke predicts ".. radiation from cosmic matter" at <20 K, but did not refer to background radiation[10]
1948 George Gamow calculates a temperature of 50 K (assuming a 3-billion year old Universe),[11] commenting it "… is in reasonable agreement with the actual temperature of interstellar space," but does not mention background radiation.
1948 Ralph Alpher and Robert Herman estimate "the temperature in the Universe" at 5 K. Although they do not specifically mention microwave background radiation, it may be inferred.[10]
1950 Ralph Alpher and Robert Herman re-re-estimate the temperature at 28 K.
1953 George Gamow estimates 7 K.[10]
1956 George Gamow estimates 6 K.[10]
1957 Tigran Shmaonov reports that "the absolute effective temperature of the radioemission background … is 4±3K".[12] It is noted that the "measurements showed that radiation intensity was independent of either time or direction of observation… it is now clear that Shmaonov did observe the cosmic microwave background at a wavelength of 3.2 cm"[13]
1960s Robert Dicke re-estimates a MBR (microwave background radiation) temperature of 40 K[10]
1964 A. G. Doroshkevich and Igor Novikov publish a brief paper, where they name the CMB radiation phenomenon as detectable.[14]
1964–65 Arno Penzias and Robert Woodrow Wilson measure the temperature to be approximately 3 K. Robert Dicke, P. J. E. Peebles, P. G. Roll and D. T. Wilkinson interpret this radiation as a signature of the big bang.
1983 RELIKT-1 Soviet CMB anisotropy experiment was launched.
1990 FIRAS measures the black body form of the CMB spectrum with exquisite precision.
January 1992 Scientists who analyzed data from RELIKT-1 spacecraft report the discovery of anisotropy at the Moscow astrophysical seminar.
April, 1992 Scientists who analyzed data from COBE DMR announce the discovery of the primary temperature anisotropy.
1999 First measurements of acoustic oscillations in the CMB anisotropy angular power spectrum from the TOCO, BOOMERANG and Maxima Experiments.
2002 Polarization discovered by DASI.[15]
2004 E-mode polarization spectrum obtained by the CBI.[16]
2005 Ralph A. Alpher is awarded the National Medal of Science for his groundbreaking work in nucleosynthesis and prediction that the universe expansion leaves behind background radiation, thus providing a model for the Big Bang theory.
2006 Two of COBE's principal investigators, George Smoot and John Mather, received the Nobel Prize in Physics in 2006 for their work on precision measurement of the CMBR.[17]
2010 The first all-sky map from the Planck telescope is released.

The cosmic microwave background was predicted in 1948 by George Gamow and Ralph Alpher, and by Alpher and Robert Herman. Moreover, Alpher and Herman were able to estimate the temperature of the cosmic microwave background to be 5 K, though two years later, they re-estimated it at 28 K.[18] Although there were several previous estimates of the temperature of space (see timeline), these suffered from two flaws. First, they were measurements of the effective temperature of space, and did not suggest that space was filled with a thermal Planck spectrum; second, they are dependent on our special place at the edge of the Milky Way galaxy and did not suggest the radiation is isotropic. Moreover, they would yield very different predictions if Earth happened to be located elsewhere in the universe.[19]

The 1948 results of Gamow and Alpher were not widely discussed. However, they were rediscovered by Yakov Zel'dovich in the early 1960s, and independently predicted by Robert Dicke at the same time. The first published recognition of the CMB radiation as a detectable phenomenon appeared in a brief paper by Soviet astrophysicists A. G. Doroshkevich and Igor Novikov, in the spring of 1964. In 1964, David Todd Wilkinson and Peter Roll, Dicke's colleagues at Princeton University, began constructing a Dicke radiometer to measure the cosmic microwave background.[20] In 1965, Arno Penzias and Robert Woodrow Wilson at the Crawford Hill location of Bell Telephone Laboratories in nearby Holmdel Township, New Jersey had built a Dicke radiometer that they intended to use for radio astronomy and satellite communication experiments. Their instrument had an excess 3.5 K antenna temperature which they could not account for. After receiving a telephone call from Crawford Hill, Dicke famously quipped: "Boys, we've been scooped."[21] A meeting between the Princeton and Crawford Hill groups determined that the antenna temperature was indeed due to the microwave background. Penzias and Wilson received the 1978 Nobel Prize in Physics for their discovery.[22]

The interpretation of the cosmic microwave background was a controversial issue in the 1960s with some proponents of the steady state theory arguing that the microwave background was the result of scattered starlight from distant galaxies. Using this model, and based on the study of narrow absorption line features in the spectra of stars, the astronomer Andrew McKellar wrote in 1941: "It can be calculated that the 'rotational temperatureˡ of interstellar space is 2 K."[23] However, during the 1970s the consensus was established that the cosmic microwave background is a remnant of the big bang. This was largely because new measurements at a range of frequencies showed that the spectrum was a thermal, black body spectrum, a result that the steady state model was unable to reproduce.

The Horn Antenna on which Penzias and Wilson discovered the cosmic microwave background.

Harrison, Peebles and Yu, and Zel'dovich realized that the early universe would have to have inhomogeneities at the level of 10−4 or 10−5.[24] Rashid Sunyaev later calculated the observable imprint that these inhomogeneities would have on the cosmic microwave background.[25] Increasingly stringent limits on the anisotropy of the cosmic microwave background were set by ground based experiments, but the anisotropy was first detected by the Differential Microwave Radiometer instrument on the COBE satellite.[26]

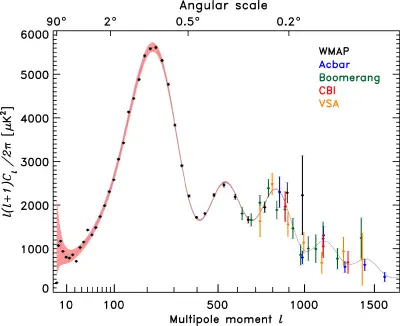
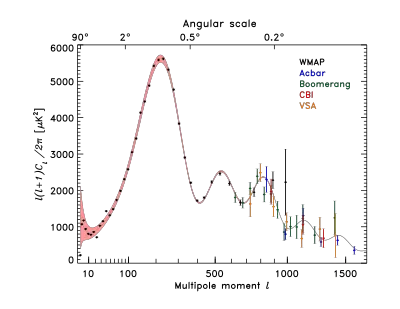
Inspired by the COBE results, a series of ground and balloon-based experiments measured cosmic microwave background anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the scale of the first acoustic peak, which COBE did not have sufficient resolution to resolve. The first peak in the anisotropy was tentatively detected by the Toco experiment and the result was confirmed by the BOOMERanG and MAXIMA experiments.[27] These measurements demonstrated that the Universe is approximately flat and were able to rule out cosmic strings as a major component of cosmic structure formation, and suggested cosmic inflation was the right theory of structure formation.

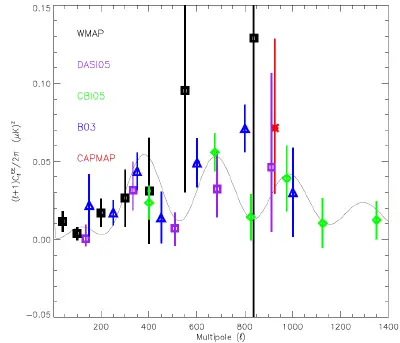
The second peak was tentatively detected by several experiments before being definitively detected by WMAP, which has also tentatively detected the third peak. Several experiments to improve measurements of the polarization and the microwave background on small angular scales are ongoing. These include DASI, WMAP, BOOMERanG and the Cosmic Background Imager. Forthcoming experiments include the Planck satellite, Atacama Cosmology Telescope, QUIET telescope and the South Pole Telescope.

Relationship to the Big Bang

Measurements of the CMB have made the inflationary Big Bang theory the standard model of the earliest eras of the universe. The standard hot big bang model of the universe requires that the initial conditions for the universe are a Gaussian random field with a nearly scale invariant or Harrison-Zel'dovich spectrum. This is, for example, a prediction of the cosmic inflation model. This means that the initial state of the universe is random, but in a clearly specified way in which the amplitude of the primeval inhomogeneities is 10-5. Therefore, meaningful statements about the inhomogeneities in the universe need to be statistical in nature. This leads to cosmic variance in which the uncertainties in the variance of the largest scale fluctuations observed in the universe are difficult to accurately compare to theory.

Temperature

The cosmic microwave background radiation and the cosmological red shift are together regarded as the best available evidence for the Big Bang (BB) theory. The discovery of the CMB in the mid-1960s curtailed interest in alternatives such as the steady state theory. The CMB gives a snapshot of the Universe when, according to standard cosmology, the temperature dropped enough to allow electrons and protons to form hydrogen atoms, thus making the universe transparent to radiation. When it originated some 400,000 years after the Big Bang — this time period is generally known as the "time of last scattering" or the period of recombination or decoupling — the temperature of the Universe was about 3,000 K. This corresponds to an energy of about 0.25 eV, which is much less than the 13.6 eV ionization energy of hydrogen. Since then, the temperature of the radiation has dropped by a factor of roughly 1100 due to the expansion of the Universe. As the universe expands, the CMB photons are redshifted, making the radiation's temperature inversely proportional to the Universe's scale length. For details about the reasoning that the radiation is evidence for the Big Bang, see Cosmic background radiation of the Big Bang.

The power spectrum of the cosmic microwave background radiation temperature anisotropy in terms of the angular scale (or multipole moment). The data shown come from the WMAP (2006), Acbar (2004) Boomerang (2005), CBI (2004) and VSA (2004) instruments.

Primary anisotropy

The anisotropy of the cosmic microwave background is divided into two sorts: primary anisotropy – which is due to effects which occur at the last scattering surface and before – and secondary anisotropy – which is due to effects, such as interactions with hot gas or gravitational potentials, between the last scattering surface and the observer.

The structure of the cosmic microwave background anisotropies is principally determined by two effects: acoustic oscillations and diffusion damping (also called collisionless damping or Silk damping). The acoustic oscillations arise because of a competition in the photon-baryon plasma in the early universe. The pressure of the photons tends to erase anisotropies, whereas the gravitational attraction of the baryons – which are moving at speeds much less than the speed of light – makes them tend to collapse to form dense haloes. These two effects compete to create acoustic oscillations which give the microwave background its characteristic peak structure. The peaks correspond, roughly, to resonances in which the photons decouple when a particular mode is at its peak amplitude.

The peaks contain interesting physical signatures. The angular scale of the first peak determines the curvature of the Universe (but not the topology of the Universe). The second peak – truly the ratio of the odd peaks to the even peaks – determines the reduced baryon density. The third peak can be used to extract information about the dark matter density.

The locations of the peaks also give important information about the nature of the primordial density perturbations. There are two fundamental types of density perturbations—called "adiabatic" and "isocurvature." A general density perturbation is a mixture of these two types, and different theories that purport to explain the primordial density perturbation spectrum predict different mixtures.

  • adiabatic density perturbations
the fractional overdensity in each matter component (baryons, photons …) is the same. That is, if there is 1 percent more energy in baryons than average in one spot, then with a pure adiabatic density perturbations there is also 1 percent more energy in photons, and 1 percent more energy in neutrinos, than average. Cosmic inflation predicts that the primordial perturbations are adiabatic.
  • isocurvature density perturbations
the sum of the fractional overdensities is zero. That is, a perturbation where at some spot there is 1 percent more energy in baryons than average, 1 percent more energy in photons than average, and 2 percent lower energy in neutrinos than average, would be a pure isocurvature perturbation. Cosmic strings would produce mostly isocurvature primordial perturbations.

The CMB spectrum is able to distinguish these two because these two types of perturbations produce different peak locations. Isocurvature density perturbations produce a series of peaks whose angular scales (l-values of the peaks) are roughly in the ratio 1 : 3 : 5 …, while adiabatic density perturbations produce peaks whose locations are in the ratio 1 : 2 : 3 ….[28] Observations are consistent with the primordial density perturbations being entirely adiabatic, providing key support for inflation, and ruling out many models of structure formation involving, for example, cosmic strings.

Collisionless damping is caused by two effects, when the treatment of the primordial plasma as a fluid begins to break down:

  • the increasing mean free path of the photons as the primordial plasma becomes increasingly rarefied in an expanding universe
  • the finite thickness of the last scattering surface (LSS), which causes the mean free path to increase rapidly during decoupling, even while some Compton scattering is still occurring.

These effects contribute about equally to the suppression of anisotropies on small scales, and give rise to the characteristic exponential damping tail seen in the very small angular scale anisotropies.

The thickness of the LSS refers to the fact that the decoupling of the photons and baryons does not happen instantaneously, but instead requires an appreciable fraction of the age of the Universe up to that era. One method to quantify exactly how long this process took uses the photon visibility function (PVF). This function is defined so that, denoting the PVF by P(t), the probability that a CMB photon last scattered between time t and t+dt is given by P(t)dt.

The maximum of the PVF (the time where it is most likely that a given CMB photon last scattered) is known quite precisely. The first-year WMAP results put the time at which P(t) is maximum as 372 +/- 14 kyr.[29] This is often taken as the "time" at which the CMB formed. However, to figure out how long it took the photons and baryons to decouple, we need a measure of the width of the PVF. The WMAP team finds that the PVF is greater than half of its maximum value (the "full width at half maximum," or FWHM) over an interval of 115 +/- 5 kyr. By this measure, decoupling took place over roughly 115,000 years, and when it was complete, the universe was roughly 487,000 years old.

Late time anisotropy

After the creation of the CMB, it is modified by several physical processes collectively referred to as late-time anisotropy or secondary anisotropy. After the emission of the CMB, ordinary matter in the universe was mostly in the form of neutral hydrogen and helium atoms, but from observations of galaxies it seems that most of the volume of the intergalactic medium (IGM) today consists of ionized material (since there are few absorption lines due to hydrogen atoms). This implies a period of reionization in which the material of the universe breaks down into hydrogen ions.

The CMB photons scatter off free charges such as electrons that are not bound in atoms. In an ionized universe, such electrons have been liberated from neutral atoms by ionizing (ultraviolet) radiation. Today these free charges are at sufficiently low density in most of the volume of the Universe that they do not measurably affect the CMB. However, if the IGM was ionized at very early times when the universe was still denser, then there are two main effects on the CMB:

  1. Small scale anisotropies are erased (just as when looking at an object through fog, details of the object appear fuzzy).
  2. The physics of how photons scatter off free electrons (Thomson scattering) induces polarization anisotropies on large angular scales. This large angle polarization is correlated with the large angle temperature perturbation.

Both of these effects have been observed by the WMAP satellite, providing evidence that the universe was ionized at very early times, at a redshift larger than 17. The detailed provenance of this early ionizing radiation is still a matter of scientific debate. It may have included starlight from the very first population of stars (population III stars), supernovae when these first stars reached the end of their lives, or the ionizing radiation produced by the accretion disks of massive black holes.

The period after the emission of the cosmic microwave background and before the observation of the first stars is semi-humorously referred to by cosmologists as the dark age, and is a period which is under intense study by astronomers (See 21 centimeter radiation).

Other effects that occur between reionization and our observation of the cosmic microwave background which cause anisotropies include the Sunyaev-Zel'dovich effect, in which a cloud of high energy electrons scatters the radiation, transferring some energy to the CMB photons, and the Sachs-Wolfe effect, which causes photons from the cosmic microwave background to be gravitationally redshifted or blue shifted due to changing gravitational fields.

E polarization measurements as of March 2006 in terms of angular scale (or multipole moment). The polarization is much more poorly measured than the temperature anisotropy.

Velocity relative to CMB anisotropy

From the CMB data it is seen that our local group of galaxies (the galactic cluster that includes the Solar System's Milky Way Galaxy) appears to be moving at 627 ± 22 km/s relative to the reference frame of the CMB (also called the CMB rest frame) in the direction of galactic longitude l = 276o ± 3o, b = 30o ± 3o.[30] This motion results in an anisotropy of the data (CMB appearing slightly warmer in the direction of movement than in the opposite direction).

The standard interpretation of this temperature variation is a simple velocity redshift and blueshift due to motion relative to the CMB, however alternative cosmological models can explain some fraction of the observed dipole temperature distribution in the CMB (see reference for one example).[31]

Polarization

The cosmic microwave background is polarized at the level of a few microkelvins. There are two types of polarization, called E-modes and B-modes. This is in analogy to electrostatics, in which the electric field (E-field) has a vanishing curl and the magnetic field (B-field) has a vanishing divergence. The E-modes arise naturally from Thomson scattering in an inhomogeneous plasma. The B-modes, which have not been measured and are thought to have an amplitude of at most a 0.1 µK, are not produced from the plasma physics alone. They are a signal from cosmic inflation and are determined by the density of primordial gravitational waves. Detecting the B-modes will be extremely difficult, particularly given that the degree of foreground contamination is unknown, and the weak gravitational lensing signal mixes the relatively strong E-mode signal with the B-mode signal.[32]

Microwave background observations

Subsequent to the discovery of the CMB, hundreds of cosmic microwave background experiments have been conducted to measure and characterize the signatures of the radiation. The most famous experiment is probably the NASA Cosmic Background Explorer (COBE) satellite that orbited in 1989–1996 and which detected and quantified the large scale anisotropies at the limit of its detection capabilities. Inspired by the initial COBE results of an extremely isotropic and homogeneous background, a series of ground- and balloon-based experiments quantified CMB anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the angular scale of the first acoustic peak, for which COBE did not have sufficient resolution. These measurements were able to rule out cosmic strings as the leading theory of cosmic structure formation, and suggested cosmic inflation was the right theory. During the 1990s, the first peak was measured with increasing sensitivity and by 2000 the BOOMERanG experiment reported that the highest power fluctuations occur at scales of approximately one degree. Together with other cosmological data, these results implied that the geometry of the Universe is flat. A number of ground-based interferometers provided measurements of the fluctuations with higher accuracy over the next three years, including the Very Small Array, Degree Angular Scale Interferometer (DASI) and the Cosmic Background Imager (CBI). DASI made the first detection of the polarization of the CMB and the CBI provided the first E-mode polarization spectrum with compelling evidence that it is out of phase with the T-mode spectrum.

In June 2001, NASA launched a second CMB space mission, WMAP, to make much more precise measurements of the large scale anisotropies over the full sky. The first results from this mission, disclosed in 2003, were detailed measurements of the angular power spectrum to below degree scales, tightly constraining various cosmological parameters. The results are broadly consistent with those expected from cosmic inflation as well as various other competing theories, and are available in detail at NASA's data center for Cosmic Microwave Background (CMB) (see links below). Although WMAP provided very accurate measurements of the large angular-scale fluctuations in the CMB (structures about as large in the sky as the moon), it did not have the angular resolution to measure the smaller scale fluctuations which had been observed using previous ground-based interferometers.

A third space mission, the Planck Surveyor, is to be launched in 2009. Planck employs both HEMT radiometers as well as bolometer technology and will measure the CMB on smaller scales than WMAP. Unlike the previous two space missions, Planck is a collaboration between NASA and ESA (the European Space Agency). Its detectors got a trial run at the Antarctic Viper telescope as ACBAR (Arcminute Cosmology Bolometer Array Receiver) experiment – which has produced the most precise measurements at small angular scales to date – and at the Archeops balloon telescope.

Additional ground-based instruments such as the South Pole Telescope in Antarctica and the proposed Clover Project, Atacama Cosmology Telescope and the QUIET telescope in Chile will provide additional data not available from satellite observations, possibly including the B-mode polarization.

Data analysis

The power spectrum of the cosmic microwave background radiation anisotropy in terms of the angular scale (or multipole moment). The data shown come from the WMAP (2006), Acbar (2004) Boomerang (2005), CBI (2004) and VSA (2004) instruments. Also shown is a theoretical model (solid line).

The analysis of cosmic microwave background data to produce maps, an angular power spectrum and ultimately cosmological parameters is a complicated, computationally difficult problem. Although computing a power spectrum from a map is in principle a simple Fourier transform, decomposing the map of the sky into spherical harmonics, in practice it is hard to take the effects of noise and foregrounds into account. In particular, these foregrounds are dominated by galactic emissions such free-free, synchrotron and dust that emit in the microwave band; in practice, the galaxy has to be removed resulting in a CMB map that is not a full-sky map. In addition, point sources like galaxies and clusters represent another source of foreground which must be removed lest they distort the short scale structure of the CMB power spectrum.

Constraints on many cosmological parameters can be obtained from their effects on the power spectrum, and results are often calculated using Markov Chain Monte Carlo sampling techniques.

Low multipoles

With the increasingly precise data provided by WMAP, there have been a number of claims that the CMB suffers from anomalies, such as non-Gaussianity. The most longstanding of these is the low-l multipole controversy. Even in the COBE map, it was observed that the quadrupole (l = 2 spherical harmonic) has a low amplitude compared to the predictions of the big bang. Some observers have pointed out that the anisotropies in the WMAP data did not appear to be consistent with the big bang picture. In particular, the quadrupole and octupole (l = 3) modes appear to have an unexplained alignment with each other and with the ecliptic plane.[33] A number of groups have suggested that this could be the signature of new physics at the largest observable scales. Ultimately, due to the foregrounds and the cosmic variance problem, the largest modes will never be as well measured as the small angular scale modes. The analyses were performed on two maps that have had the foregrounds removed as best as is possible: the "internal linear combination" map of the WMAP collaboration and a similar map prepared by Max Tegmark and others.[34] Later analyses have pointed out that these are the modes most susceptible to foreground contamination from synchrotron, dust and free-free emission, and from experimental uncertainty in the monopole and dipole. A full Bayesian analysis of the WMAP power spectrum demonstrates that the quadrupole prediction of Lambda-CDM cosmology is consistent with the data at the 10 percent level and that the octupole is not remarkable[35]. Carefully accounting for the procedure used to remove the foregrounds from the full sky map further reduces the significance of the alignment by about 5 percent.[36]

Notes

  1. ↑ The Cosmic Microwave Background Radiation Retrieved January 17, 2023.
  2. ↑ A.A. Penzias and R.W. Wilson, A Measurement of Excess Antenna Temperature at 4080 Mc/s. Astrophysical Journal 142 (1965):419–421.
  3. ↑ This ignores the dipole anisotropy, which is due to the Doppler shift of the microwave background radiation due to our peculiar velocity relative to the comoving cosmic rest frame. This feature is consistent with the Earth moving at some 380 km/s towards the constellation Virgo.
  4. ↑ D.J. Fixsen, et al., The Cosmic Microwave Background Spectrum from the full COBE FIRAS data set. Astrophysical Journal 473 (1996):576–587.
  5. ↑ The energy density of a black-body spectrum is , where T is the temperature, is the Boltzmann constant, is the Planck constant and c is the speed of light. This can be related to the critical density of the universe using the parameters of the Lambda-CDM model.
  6. ↑ G. Hinshaw et al., First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: the angular power spectrum. Astrophysical Journal Supplement 148 (2003):135–159.
  7. ↑ D.N. Spergel, et al., First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: determination of cosmological parameters Astrophysical Journal Supplement 148 (2003):175–194. Retrieved January 17, 2023.
  8. ↑ A. McKellar, Dominion Astrophysics Observatory Journal, Victoria, British Columbia VII(15) (1941):251. McKellar was attempting to measure the average temperature of the interstellar medium. It is unlikely that he had any idea of the cosmological implications of his measurement, but it was a remarkable and sophisticated achievement.
  9. ↑ Steven Weinberg, Gravitation and Cosmology: Principles and applications of the general theory of relativity (New York, NY: John Wiley & sons Inc., 1972, ISBN 9780471925675), 514.
  10. ↑ 10.0 10.1 10.2 10.3 10.4 Helge Kragh, Cosmology and Controversy: The historical development of two theories of the universe (Princeton, NJ: Princeton University Press, 1999, ISBN 069100546X). "In 1946, Robert Dicke and coworkers at MIT tested equipment that could test a cosmic microwave background of intensity corresponding to about 20K in the microwave region. However, they did not refer to such a background, but only to 'radiation from cosmic matter.' Also, this work was unrelated to cosmology and is only mentioned because it suggests that by 1950, detection of the background radiation might have been technically possible, and also because of Dicke's later role in the discovery."
  11. ↑ George Gamow, The Creation Of The Universe (Mineola, NY: Dover Publications, 2004, ISBN 0486438686), 40.
  12. ↑ Tigran Shmaonov, Pribory i Teknika Eksperienta (1957).
  13. ↑ Pavel D. Naselsky, Dmitry I. Novikov, and Igor D. Novikov, The Physics of the Cosmic Microwave Background (Cambridge, UK: Cambridge University Press, 2006, ISBN 0521855500).
  14. ↑ A.G. Doroshkevich and I.D. Novikov, Mean Density of Radiation in the Metagalaxy and Certain Problems in Relativistic Cosmology. Sov. Phys. Doklady 9 (1964):111. Retrieved January 17, 2023.
  15. ↑ J. Kovac et al., Detection of polarization in the cosmic microwave background using DASI. Nature. 420 (2002):772–787.
  16. ↑ A. Readhead, et al., Polarization observations with the Cosmic Background Imager. Science. 306 (2004):836–844.
  17. ↑ Robert Sanders and Jeffery Kahn, UC Berkeley & LBL scientist George Smoot awarded Nobel Prize in Physics UC Berkeley News, October 3, 2006. Retrieved January 17, 2023.
  18. ↑ G. Gamow, The Origin of Elements and the Separation of Galaxies. Physical Review 74 (1948):505; G. Gamow, The evolution of the universe. Nature 162 (1948):680; R.A. Alpher and R. Herman, On the Relative Abundance of the Elements. Physical Review 74 (1948):1577.
  19. ↑ A.K.T. Assis, and M.C.D. Neves,History of the 2.7 K Temperature Prior to Penzias and Wilson APEIRON 2(3) (July 1995):79-87. Retrieved January 17, 2023.
  20. ↑ R.H. Dicke, The measurement of thermal radiation at microwave frequencies. Rev. Sci. Instrum 17 (1946):268. This basic design for a radiometer has been used in most subsequent cosmic microwave background experiments.
  21. ↑ A.A. Penzias and R.W. Wilson. A Measurement of Excess Antenna Temperature at 4080 Mc/s. Astrophysical Journal 142 (1965):419; R.H. Dicke, P.J.E. Peebles, P.G. Roll, and D.T. Wilkinson, Cosmic Black-Body Radiation. Astrophysical Journal 142 (1965):414. The history is given in P.J.E. Peebles, Principles of Physical Cosmology (Princeton, NJ: Princeton University Press, 1993, ISBN 9780691019338).
  22. ↑ The Nobel Prize in Physics 1978 The Nobel Prize. Retrieved January 17, 2023.
  23. ↑ A. McKellar, Publ. Dominion Astrophys. Obs. 7 (1941):251.
  24. ↑ E.R. Harrison, Fluctuations at the threshold of classical cosmology. Phys. Rev. D1 (1970):2726.; P.J.E. Peebles and J.T. Yu. Primeval adiabatic perturbation in an expanding universe. Astrophysical Journal 162 (1970):815; Y.B. Zel'dovich, A hypothesis, unifying the structure and entropy of the universe. Monthly Notices of the Royal Astronomical Society. (1972):160.
  25. ↑ R.A. Sunyaev, "Fluctuations of the microwave background radiation," in M.S. Longair and J. Einasto (eds.), Large Scale Structure of the Universe. (Dordrecht, NL: Reidel, 1978, ISBN 9789027708953). While this is the first paper to discuss the detailed observational imprint of density inhomogeneities as anisotropies in the cosmic microwave background, some of the groundwork was laid in Peebles and Yu, above.
  26. ↑ George Smoot et al., Structure in the COBE DMR first year maps. Astrophysical Journal 396 (1992):L1–L5; C.L. Bennett et al., Four year COBE DMR cosmic microwave background observations: maps and basic results. Astrophysical Journal 464 (1996):L1–L4.
  27. ↑ A.D. Miller et al., A measurement of the angular power spectrum of the cosmic microwave background from l = 100 to 400. Astrophysical Journal 524 (1999):L1–L4; P. de Bernardis, et al., A flat universe from high-resolution maps of the cosmic microwave background Nature. 404 (2000):955; S. Hanany et al., MAXIMA-1: A measurement of the cosmic microwave background anisotropy on angular scales of 10'-5°. Astrophysical Journal. 545 (2000):L5–L9.
  28. ↑ Wayne Hu and Martin White, Acoustic Signatures in the Cosmic Microwave Background. Astrophysical Journal 471 (1996):30.
  29. ↑ WMAP Collaboration, First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 148 (2003):175.
  30. ↑ A. Kogut et al., Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps. Astrophysical Journal 419 (1993):1. Retrieved January 17, 2023.
  31. ↑ Kaiki Taro Inoue and Joseph Silk, Local Voids as the Origin of Large-Angle Cosmic Microwave Background Anomalies: The Effect of a Cosmological Constant Astrophysical Journal 664(2) (2007):650-659.
  32. ↑ A. Lewis and A. Challinor, Weak gravitational lensing of the CMB. Phys. Rep. 429 (2006):1–65.
  33. ↑ A. de Oliveira-Costa, M. Tegmark, M. Zaldarriga, and A. Hamilton, The significance of the largest scale CMB fluctuations in WMAP. Phys. Rev. (2004):D69:063516; D.J. Schwarz, G.D. Starkman, D. Huterer, and C. J. Copi, Is the low-l microwave background cosmic? Phys. Rev. Lett.. 93 (2004):221301; P. Bielewicz, K.M. Gorski and A.J. Banday, Low-order multipole maps of CMB anisotropy derived from WMAP. Mon. Not. Roy. Astron. Soc. 355 (2004):1283.
  34. ↑ C.L. Bennett et al, (WMAP collaboration), First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: preliminary maps and basic results. Astrophysical Journal Supplement 148 (2003):1; M. Tegmark, A. de Oliveira-Costa, and A. Hamilton, A high resolution foreground cleaned CMB map from WMAP. Phys. Rev. (2003): D68:123523; G. Hinshaw, et al., Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Temperature Analysis, (2007). The first year WMAP paper warns: "the statistics of this internal linear combination map are complex and inappropriate for most CMB analyses." The third year paper states: "Not surprisingly, the two most contaminated multipoles are the quadrupole and octopole, which most closely trace the galactic plane morphology."
  35. ↑ I. O'Dwyer et al., Bayesian Power Spectrum Analysis of the First-Year Wilkinson Microwave Anisotropy Probe Data. Astrophys. J. Lett. 617 (2004):L99–L102.
  36. ↑ A. Slosar and U. Seljak. Assessing the effects of foregrounds and sky removal in WMAP. Phys. Rev. D70 (2004):083002; P. Bielewicz, H.K. Eriksen, A.J. Banday, K.M. Gorski, and P.B. Lilije, Multipole vector anomalies in the first-year WMAP data: a cut-sky analysis. Astrophys. J. 635 (2005):750–60; C.J. Copi, D. Huterer, D.J. Schwarz, and G.D. Starkman, On the large-angle anomalies of the microwave sky. Mon. Not. Roy. Astron. Soc. 367 (2006):79–102.

References
ISBN links support NWE through referral fees

  • Barrow, John D. The Origin of the Universe. (Science Masters Series.) New York, NY: Basic Books, 1994. ISBN 0465053548
  • Gamow, Gamov. The Creation Of The Universe. reprint ed. Mineola, NY: Dover Publications, 2004. ISBN 0486438686
  • Kolb, Edward W., and Michael Stanley Turner. The Early Universe. (Frontiers in Physics, v. 69.) Reading, MA: Addison-Wesley, 1990. ISBN 0201116030
  • Kragh, Helge. Cosmology and Controversy: The historical development of two theories of the universe. Princeton, NJ: Princeton University Press, 1999. ISBN 069100546X
  • Longair, Malcolm S., and J. Einasto (eds.). Large Scale Structure of the Universe. Dordrecht, NL: Reidel, 1978. ISBN 978-9027708953
  • Mather, John C., and John Boslough. The Very First Light: The True Inside Story of the Scientific Journey Back to the Dawn of the Universe. New York, NY: Basic Books, 1996. ISBN 0465015751
  • Naselsky, Pavel D., Dmitry I. Novikov, and Igor D. Novikov. The Physics of the Cosmic Microwave Background. Cambridge, UK: Cambridge University Press, 2006. ISBN 0521855500
  • Peacock, John A. Cosmological Physics. Cambridge, UK: Cambridge University Press, 1999. ISBN 0521422701
  • Peebles, P.J.E. Principles of physical cosmology. Princeton, NJ: Princeton Univ. Pr., 1993. ISBN 978-0691019338
  • Weinberg, Steven. Gravitation and Cosmology: Principles and applications of the general theory of relativity. New York, NY: John Wiley & sons Inc., 1972. ISBN 978-0471925675

External links

All links retrieved January 10, 2024.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

The history of this article since it was imported to New World Encyclopedia:

Note: Some restrictions may apply to use of individual images which are separately licensed.

Retrieved from https://www.newworldencyclopedia.org/p/index.php?title=Cosmic_microwave_background_radiation&oldid=1132811

Content is available under Creative Commons Attribution/Share-Alike License; additional terms may apply. See Terms of Use for details.
Copyright Logo
Powered by MediaWiki