Ptolemy
- This article is about Ptolemy the astronomer, mathematician, and geographer. He is not to be confused with Ptolemy I Soter, a Macedonian general who became king of Egypt in 305 B.C.E., or other Egyptian rulers in the Ptolemaic dynasty.
Ptolemy, or in Latin Claudius Ptolemaeus (ca. 90 – ca. 168 C.E.), was a mathematician, philosopher, geographer, map maker, astronomer, theologian, and astrologer who lived in Alexandria, Egypt. He is most remembered because of his development of the geocentric (Earth-centered) cosmological system, known as the Ptolemaic system or Ptolemaic cosmology, which was one of the most influential and longest-lasting, intellectual-scientific achievements in human history. Although his model of the universe was erroneous, he based his theory on observations that he and others had made, and he provided a mathematical foundation that made a powerful case in support of the geocentric paradigm and ensured its continued use well into the future. He may have been a Hellenized Egyptian. Aside from that, almost nothing is known about Ptolemy's life, family background, or physical appearance.
Ptolemy’s treatises
Ptolemy was the author of numerous scientific treatises, at least three of which were of continuing importance to later Islamic and European science. The first was the astronomical treatise originally called He mathematike syntaxis ("The Mathematical Collection"), which came eventually to be known as Ho megas astronomos ("The Great Astronomer"). During the ninth century, Arab astronomers used the Greek superlative term Megiste for this work, which, when the definite article al was prefixed to it, became Almagest, the name by which it is generally known today. His second major work was Geographia, and a third of his noteworthy works was a set of books on geometry. He also wrote a treatise on astrology known as the Tetrabiblos, and additional works on music, optics, and other subjects.
The first chapter of Almagest, his most important work, contains a discussion of epistemology and philosophy. Two themes are paramount and woven together there: the organization of philosophy and his reason for studying mathematics. In the ancient period, "philosophy" included much more than is usually encompassed by that term today—it meant the whole of human knowledge and wisdom.
Aristotle—the only philosopher to whom Ptolemy refers explicitly—had distinguished between practical and theoretical philosophy, and Ptolemy used that distinction, noting that education is needed for theoretical philosophy but not for practical philosophy. Ptolemy also wrote that Aristotle had divided theoretical philosophy into three branches: physics, mathematics, and theology. Ptolemy followed that tripartite division, claiming that theology is the branch of theoretical philosophy that investigates the first cause of the first motion of the universe (Taub 1993).
Both Ptolemy and Aristotle held theology to be one of the main branches of philosophy. It should be noted, however, that they were Greek pagans who held to the Greek pantheon of gods and the Greek understanding of the behavior and activity of the gods. It would be a mistake, therefore, to think that their theological investigations and speculations were equivalent or similar to what Jewish, Christian, or Muslim theologians or scholars would say about either the methods or objects of theology. Yet, by putting theology in with what they called physics (or what is today called natural science) and mathematics as the central concerns of philosophy, Ptolemy and Aristotle differed from present-day secular scientists, philosophers, and epistemologists, who have no role for or interest in theology.
Astronomy
In the Almagest, one of the most influential books of classical antiquity, Ptolemy compiled the astronomical knowledge of the ancient Greek and Babylonian world; he relied mainly on the work of Hipparchus of three centuries earlier. It was preserved, like most of classical Greek science, in Arabic manuscripts (hence its familiar name) and made available in Latin translation (by Gerard of Cremona) in the twelfth century.
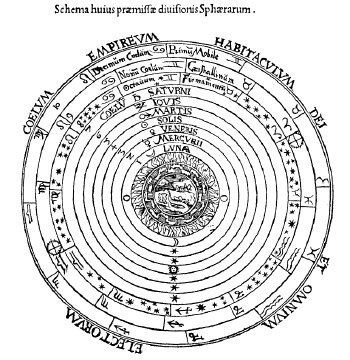
The Almagest is divided into 13 books. Each of them deals with astronomical concepts concerning the stars and objects in the solar system. Ptolemy's geocentric model or theory put the Earth at the center of the universe—a theory often known as the Ptolemaic System, or Ptolemaic Cosmology. This view was almost universally held until it was superseded by the heliocentric (Sun-centered) solar system, first put forth by Copernicus in the first three decades of the sixteenth century.
In Ptolemy's cosmology, the Earth occupies the center of the universe, while other heavenly bodies lie beyond it in the following order: the Moon, Mercury, Venus, Sun, Mars, Jupiter, and Saturn—in his day, only five planets were known to exist. To account for the movements of these bodies, the Ptolemaic system used large circles centered on the Earth, along with smaller circles, or epicycles, that moved around the circumferences of the larger circles.
Ptolemy gave various reasons why the Earth must be both at the center of the universe and immovable. One argument was that because all bodies fall to the center of the universe, if the Earth were not at the center, things would not fall to the Earth, but the Earth itself would fall. He also argued that if the Earth moved, then things thrown vertically upward would not fall to the place from which they had been thrown, as they were observed to do. Scientists now recognize that all those reasons are false or mistaken.
Following Aristotle, Ptolemy and those who accepted his view made a number of philosophical assumptions underlying their cosmology. First, they assumed that unless things are pushed and made to move, their natural state is stationary. Second, they assumed that if humans were to occupy the highest position in the universe, then they had to occupy the physical center of the universe—meaning that the Earth had to be at the center. Third, they assumed that the most perfect motion was circular motion. It would not occur to people until the work of Kepler at the beginning of the seventeenth century that the motion of the planets is elliptical instead of circular, and even Kepler took some time to arrive at that insight. All those assumptions are now rejected as being false.
Ptolemy's computational methods (supplemented in the twelfth century with the Arabic computational Tables of Toledo) were of sufficient accuracy to satisfy the needs of astronomers, astrologers, and navigators, until the time of the great explorations. They were also adopted in the Arab world and India. The Almagest also contains a star catalog, which is probably an updated version of a catalog created by Hipparchus. Its list of 48 constellations is ancestral to the modern system of constellations, but unlike the modern system, they covered only the sky Ptolemy could see, not the whole sky.
The Planetary Hypotheses (Ancient Greek: Ὑποθέσεις τῶν πλανωμένων, lit. "Hypotheses of the Planets") is a cosmological work, probably one of the last written by Ptolemy, in two books dealing with the structure of the universe and the laws that govern celestial motion. Ptolemy goes beyond the mathematical models of the Almagest to present a physical realization of the universe as a set of nested spheres, in which he used the epicycles of his planetary model to compute the dimensions of the universe. He estimated the Sun was at an average distance of 1,210 Earth radii (now known to actually be ~23,450 radii), while the radius of the sphere of the fixed stars was 20,000 times the radius of the Earth (Goldstein 1967).
The work is also notable for having descriptions on how to build instruments to depict the planets and their movements from a geocentric perspective, much like an orrery would have done for a heliocentric one, presumably for didactic purposes.
Geography
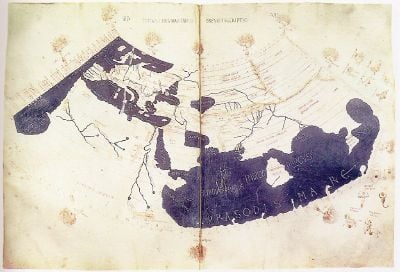
A second of Ptolemy's influential works is his Geographia, a thorough discussion of the geographic knowledge of the Greco-Roman world. This, too, is a compilation of what was known about the world's geography in the Roman Empire during his time. He relied mainly on the work of an earlier geographer, Marinos of Tyre, and on gazetteers of the Roman and ancient Persian empires, but most of his sources beyond the perimeter of the Roman Empire were unreliable.
The first part of the Geographia is a discussion of the data and methods he used. As with the model of the solar system in the Almagest, Ptolemy put all this information into a grand scheme. He assigned coordinates to all the places and geographic features he knew, in a grid that spanned the globe. Latitude was measured from the equator, as it is today, but Ptolemy preferred to express it as the length of the longest day rather than degrees of arc. [The length of the midsummer day increases from 12h to 24h as you go from the equator to the polar circle.] He put the meridian of 0 longitude at the westernmost land he knew, namely, the Canary Islands.
Ptolemy also devised and provided instructions on how to create maps of the whole inhabited world (oikoumenè) as well as the Roman provinces. In the second part of the Geographia, he provided the necessary topographic lists, along with captions for the maps. His oikoumenè spanned 180 degrees of longitude, from the Canary Islands in the Atlantic Ocean to the middle of China; and about 80 degrees of latitude, from the Arctic to the East Indies and deep into Africa. Ptolemy was well aware that he knew about only a quarter of the globe, and he knew that his information did not extend to the Eastern Sea.
The maps in surviving manuscripts of Ptolemy's Geographia, however, date only from about 1300, after the text was rediscovered by Maximus Planudes. It seems likely that the topographical tables in books two through seven are cumulative texts—texts that were altered and added to as new knowledge became available in the centuries after Ptolemy (Bagrow 1945). This means that information contained in different parts of the Geographia is likely to be of different dates.
Maps based on scientific principles had been made since the time of Eratosthenes (third century B.C.E.), but Ptolemy improved on the projections. It is known that a world map based on the Geographia was on display in Autun, France, in late Roman times. In the fifteenth century, the Geographia began to be printed with engraved maps. The earliest printed edition with engraved maps was produced in Bologna in 1477, followed quickly by a Roman edition in 1478 (Campbell, 1987). An edition printed at Ulm in 1482, including woodcut maps, was the first one printed north of the Alps. The maps look distorted compared to modern maps because Ptolemy's data were inaccurate. One reason is that Ptolemy underestimated the size of the Earth—while Eratosthenes found 700 stadia for a degree on the globe, in the Geographia Ptolemy used 500 stadia. It is not certain if these geographers used the same value for one stadion, but there is no direct evidence of more than one value of the stadion. If they both used the traditional Olympic stadion of about 185 meters, then the older estimate is one-sixth too large, and Ptolemy's value is one-sixth too small.
Because Ptolemy derived most of his topographic coordinates by converting measured distances to angles, his maps are distorted. His values for latitude were in error by up to two degrees. For longitude, his measures were even worse, because there was no reliable method to determine geographic longitude; Ptolemy was well aware of this. It remained a problem in geography until the invention of chronometers at the end of the eighteenth century. It must be added that his original topographic list cannot be reconstructed. The long tables with numbers were transmitted to posterity through copies containing many scribal errors, and people have always been adding to or improving the topographic data. This can be viewed as a testimony to the persistent popularity of this influential work.
Geometry
Ptolemy was a first-rate geometer and mathematician who devised important new geometrical proofs and theorems. In one book, entitled Analemma, he discussed projections of points on a celestial sphere. In another work, Planispherium, he studied stereographic projection, or the forms of solid objects represented on a plane.
Astrology
Another of Ptolemy's noteworthy works is his treatise on astrology known as the Tetrabiblos ("Four books," derived from the Greek words tetra, meaning "four", and biblos, meaning "book"). In it, he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. The Tetrabiblos was the most popular astrological work of antiquity and also enjoyed great influence in the Islamic world and the medieval Latin West. It was continually reprinted.
The great popularity of this treatise might be attributed to its exposition of the art of astrology and its being a compendium of astrological lore, rather than a manual. It speaks in general terms, avoiding illustrations and details of practice. Ptolemy was concerned about defending astrology by defining its limits, compiling astronomical data that he thought were reliable and dismissing some practices (such as considering the numerological significance of names) that he believed to be without sound basis.
Much of the content of the Tetrabiblos may well have been collected from earlier sources. Ptolemy's achievement was to order his material in a systematic way, showing how the subject could, in his view, be rationalized. It is, indeed, presented as the second part of the study of astronomy, of which the Almagest was the first, concerned with the influences of the celestial bodies in the sublunar sphere. Thus explanations of a sort are provided for the astrological effects of the planets, based upon their combined effects of heating, cooling, moistening, and drying.
Ptolemy's astrological outlook was quite practical. He thought that astrology was like medicine in being conjectural, because of the many variable factors to be taken into account. People’s personalities were affected by their race, country, and upbringing as much as if not more than the positions of the Sun, Moon, and planets at the precise moment of their birth. So Ptolemy saw astrology as something to be used in life but in no way relied on entirely.
The Tetrabiblos did not quite attain the unrivaled status of the Almagest, perhaps because it did not cover some popular areas of the subject, particularly horary astrology (involving interpretation of astrological charts to determine the outcome of a course of action to be initiated at a particular moment), electional astrology (involving the selection of an auspicious time to conduct a specific life-activity by a specific person), and medical astrology.
Music
Ptolemy also wrote an influential work, Harmonics, on music theory. After criticizing the approaches of his predecessors, Ptolemy argued for basing musical intervals on mathematical ratios (in contrast to the followers of Aristoxenus) backed up by empirical observation, in contrast to the overly theoretical approach of the Pythagoreans. He presented his own divisions of the tetrachord and octave, which he derived with the help of a monochord. Ptolemy's astronomical interests also appeared in a discussion of the music of the spheres.
Optics
Ptolemy's Optics is a work in five books that survives only as a poor Arabic translation. In it, he wrote about some of the properties of light, including reflection, refraction (the way light changes direction when passing from one medium to another of different density), and color. This was the first work on record that attempted to account for the observed phenomenon of the refraction of light. Recent attention to Ptolemy's Optics shows its "sophisticated observational basis" and that Ptolemy had conducted "a series of carefully contrived experiments measuring refraction from air to water, air to glass, and water to glass" (Smith 1999).
Named after Ptolemy
ReferencesISBN links support NWE through referral fees
Texts and translations:
- Berggren, J. Lennart and Alexander Jones. 2000. Ptolemy's Geography: An Annotated Translation of the Theoretical Chapters. Princeton: Princeton University Press. ISBN 0691010420
- Nobbe, C. F. A. (ed.). 1843. Claudii Ptolemaei Geographia. 3 vols. Lipsiae (Leipzig): Carolus Tauchnitus. (The most recent edition of the complete Greek text)
- Stevenson, Edward Luther (trans. and ed.). 1932. Claudius Ptolemy: The Geography. New York Public Library. Reprint: Dover, 1991. (This is the only complete English translation of Ptolemy's most famous work. Unfortunately, it is marred by numerous mistakes and the place names are given in Latinized forms, rather than in the original Greek).
Other references:
- Bagrow, L. 1945. The Origin of Ptolemy's Geographia. Geografiska Annaler 27:318-387.
- Campbell, T. 1987. The Earliest Printed Maps. British Museum Press.
- Gingrich, Owen. 1997. The Eye of Heaven: Ptolemy, Copernicus, Kepler. New York: The American Institute of Physics. ISBN 978-0883188637
- Goldstein, Bernard R. (ed.). 1967. The Arabic Version of Ptolemy's Planetary Hypotheses, Transactions of the American Philosophical Society 57(4): 9–12.
- Smith, A. Mark. 1999. Ptolemy and the Foundations of Ancient Mathematical Optics: A Source Based Guided Study. Transactions of the American Philosophical Society Held at Philadelphia For Promoting Useful Knowledge, Vol. 89(3). Philadelphia: American Philosophical Society.
- Taub, Liba Chaia. 1993. Ptolemy's Universe: The Natural Philosophical and Ethical Foundations of Ptolemy's Astronomy. Chicago and LaSalle, IL: Open Court. ISBN 978-0812692280
External links
All links retrieved December 2, 2022.
- Ptolemy's Tetrabiblos at LacusCurtius (English translation, with introductory material)
- Ptolemy's Geography at LacusCurtius (English translation, incomplete)
- The Life and Work of Ptolemy SkyScript
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.