Angular momentum

This gyroscope remains upright while spinning due to its angular momentum.

In physics, the angular momentum of an object rotating about some reference point is the measure of the extent to which the object will continue to rotate about that point unless acted upon by an external torque.

In particular, if a point mass rotates about an axis, then the angular momentum with respect to a point on the axis is related to the mass of the object, the velocity and the distance of the mass to the axis.

Angular momentum is important in physics because it is a conserved quantity: a system's angular momentum stays constant unless an external torque acts on it. Torque is the rate at which angular momentum is transferred in or out of the system. When a rigid body rotates, its resistance to a change in its rotational motion is measured by its moment of inertia.

Angular momentum is an important concept in both physics and engineering, with numerous applications. For example, the kinetic energy stored in a massive rotating object such as a flywheel is proportional to the square of the angular momentum.

Conservation of angular momentum also explains many phenomena in sports and nature.

Angular momentum in classical mechanics

Relationship between force (F), torque (τ), and momentum vectors (p and L) in a rotating system

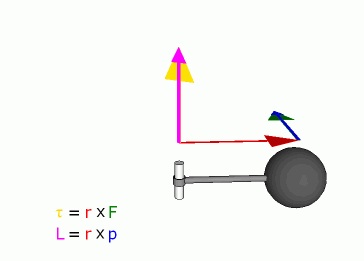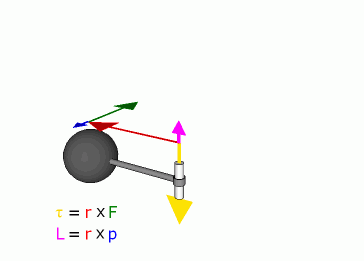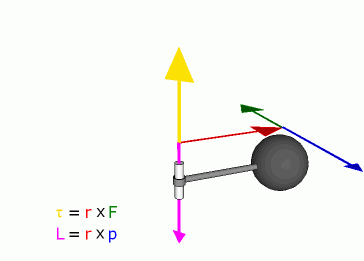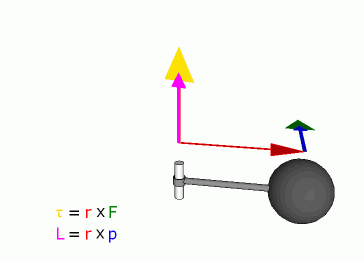
Definition

Angular momentum of a particle about some origin is defined as:

$\mathbf {L} =\mathbf {r} \times \mathbf {p}$

where:

$\mathbf {L}$ is the angular momentum of the particle,

$\mathbf {r}$ is the position of the particle expressed as a displacement vector from the origin,

$\mathbf {p}$ is the linear momentum of the particle, and

$\times \,$ is the vector cross product.

The derived SI units of angular momentum are newton·metre·seconds; N·m·s (kgm²s^-1).

Because of the cross product, L is a vector perpendicular to both the radial vector r and the momentum vector p.

If a system consists of several particles, the total angular momentum about an origin can be obtained by adding all the angular momenta of the constituent particles. Angular momentum can also be calculated by multiplying the square of the displacement r, the mass of the particle and the angular velocity.

Orbital and spin angular momentum

It is very often convenient to consider the angular momentum of a collection of particles about their center of mass, since this simplifies the mathematics considerably. The angular momentum of a collection of particles is the sum of the angular momenta of each particle:

$\mathbf {L} =\sum _{i}\mathbf {R} _{i}\times m_{i}\mathbf {V} _{i}$

where $R_{i}$ is the distance of particle i from the reference point, $m_{i}$ is its mass, and $V_{i}$ is its velocity. The center of mass is defined by:

$\mathbf {R} ={\frac {1}{M}}\sum _{i}m_{i}\mathbf {R} _{i}$

If we define $\mathbf {r} _{i}$ as the displacement of particle i from the center of mass, and $\mathbf {v} _{i}$ as the velocity of particle i with respect to the center of mass, then we have

$\mathbf {R} _{i}=\mathbf {R} +\mathbf {r} _{i}\,$   and    $\mathbf {V} _{i}=\mathbf {V} +\mathbf {v} _{i}\,$

so that the total angular momentum is

$\mathbf {L} =\sum _{i}(\mathbf {R} +\mathbf {r} _{i})\times m_{i}(\mathbf {V} +\mathbf {v} _{i})=\left(\mathbf {R} \times M\mathbf {V} \right)+\left(\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right)$

The first term is just the angular momentum of the center of mass. It is the same angular momentum one would obtain if there were just one particle of mass M moving at velocity V located at the center of mass. The second term is the angular momentum that is the result of the particles spinning about their center of mass. This second term can be even further simplified if the particles form a rigid body. An analogous result is obtained for a continuous distribution of matter. DOES THIS MEAN A SOLID OBJECT ?

Fixed axis of rotation

For many applications where one is only concerned about rotation around one axis, it is sufficient to discard the pseudovector nature of angular momentum, and treat it like a scalar where it is positive when it corresponds to a counter-clockwise rotations, and negative clockwise. To do this, just take the definition of the cross product and discard the unit vector, so that angular momentum becomes:

$L=|\mathbf {r} ||\mathbf {p} |\sin \theta _{r,p}$

where θ_r,p is the angle between r and p measured from r to p; an important distinction because without it, the sign of the cross product would be meaningless. From the above, it is possible to reformulate the definition to either of the following:

$L=\pm |\mathbf {p} ||\mathbf {r} _{\perp }|$

where r_⊥ is called the perpendicular lever arm distance to p.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

$\mathbf {L} =I\mathbf {\omega }$

where

$I\,$ is the moment of inertia of the object

$\mathbf {\omega }$ is the angular velocity.

Conservation of angular momentum

The torque caused by the two opposing forces F_g and -F_g causes a change in the angular momentum L in the direction of that torque (since torque is the time derivative of angular momentum). This causes the top to precess.

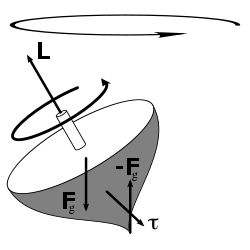
In a closed system angular momentum is constant. This conservation law mathematically follows from continuous directional symmetry of space (no direction in space is any different from any other direction). See Noether's theorem.

The time derivative of angular momentum is called torque:

$\tau ={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F}$

So requiring the system to be "closed" here is mathematically equivalent to zero external torque acting on the system:

$\mathbf {L} _{\mathrm {system} }=\mathrm {constant} \leftrightarrow \sum \tau _{\mathrm {ext} }=0$

where $\tau _{ext}$ is any torque applied to the system of particles.

In orbits, the angular momentum is distributed between the spin of the planet itself and the angular momentum of its orbit:

$\mathbf {L} _{\mathrm {total} }=\mathbf {L} _{\mathrm {spin} }+\mathbf {L} _{\mathrm {orbit} }$;

If a planet is found to rotate slower than expected, then astronomers suspect that the planet is accompanied by a satellite, because the total angular momentum is shared between the planet and its satellite in order to be conserved.

The conservation of angular momentum is used extensively in analyzing what is called central force motion. If the net force on some body is directed always toward some fixed point, the center, then there is no torque on the body with respect to the center, and so the angular momentum of the body about the center is constant. Constant angular momentum is extremely useful when dealing with the orbits of planets and satellites, and also when analyzing the Bohr model of the atom.

The conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs close to the vertical axis of rotation. By bringing part of mass of her body closer to the axis she decreases her body's moment of inertia. Because angular momentum is constant in the absence of external torques, the angular velocity (rotational speed) of the skater has to increase.

The same phenomenon results in extremely fast spin of compact stars (like white dwarfs, neutron stars and black holes) when they are formed out of much larger and slower rotating stars (indeed, decreasing the size of object 10⁴ times results in increase of its angular velocity by the factor 10⁸).

Angular momentum in quantum mechanics

Basic definition

The classical definition of angular momentum as $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ depends on six numbers: $r_{x}$, $r_{y}$, $r_{z}$, $p_{x}$, $p_{y}$, and $p_{z}$. Translating this into quantum-mechanical terms, the Heisenberg uncertainty principle tells us that it is not possible for all six of these numbers to be measured simultaneously with arbitrary precision. Therefore, there are limits to what can be known or measured about a particle's angular momentum. It turns out that the best that one can do is to simultaneously measure both the angular momentum vector's magnitude and its component along one axis.

Mathematically, angular momentum in quantum mechanics is defined like momentum - not as a quantity but as an operator on the wave function:

$\mathbf {L} =\mathbf {r} \times \mathbf {p}$

where r and p are the position and momentum operators respectively. In particular, for a single particle with no electric charge and no spin, the angular momentum operator can be written in the position basis as

$\mathbf {L} =-i\hbar (\mathbf {r} \times \nabla )$

where $\nabla$ is the gradient operator, read as "del," "grad," or "nabla." This is a commonly encountered form of the angular momentum operator, though not the most general one. It satisfies the following commutation relations

$[L_{i},L_{j}]=i\hbar \epsilon _{ijk}L_{k}$

from which follows

$\left[L_{i},L^{2}\right]=0$

See also

• Angular momentum coupling
• Angular velocity
• Momentum
• Rotational energy
• Torque
• Noether's theorem

References

ISBN links support NWE through referral fees

<<Please reformat each reference according to our guidelines. For references given in the "cite book" format, extract the info from them and place in our format.>>

• E. U. Condon and G. H. Shortley, The Theory of Atomic Spectra, (1935) Cambridge at the University Press, ISBN 0-521-09209-4 See chapter 3.
• Edmonds, A.R., Angular Momentum in Quantum Mechanics, (1957) Princeton University Press, ISBN 0-691-07912-9.
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7. 
• Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4. 

External links

• Conservation of Angular Momentum - a chapter from an online textbook

• Angular Momentum in a Collision Process - derivation of the three dimensional case

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Angular momentum  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Angular momentum"

Note: Some restrictions may apply to use of individual images which are separately licensed.