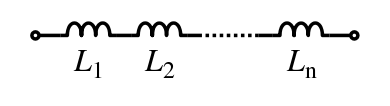Inductor
| Inductor | |
 A selection of low-value inductors | |
| Type | Passive |
|---|---|
| Electronic symbol | |
An inductor is a passive electrical component that can store energy in a magnetic field created by passing an electric current through it. A simple inductor is a coil of wire. When an electric current is passed through the coil, a magnetic field is formed around it. This magnetic field causes the inductor to resist changes in the amount of current passing through it.
An inductor's ability to store magnetic energy is measured by its inductance, in units of henries. The inductance of a coil is directly proportional to the number of turns in the coil. Inductance also varies with the coil's radius and the material (or "core") around which the coil is wound.
Inductors are widely used in analog circuits and signal processing. Large inductors, in combination with capacitors, are useful as chokes in power supplies, to remove fluctuations from direct current output. Small inductor/capacitor combinations are useful in making tuned circuits for radio reception and broadcasting. In addition, inductors are employed in transformers for power grids, and as energy storage devices in some switched-mode power supplies.
Overview
When an electric current first begins to pass through an inductor (coil of wire), the inductor resists the flow of current, as a magnetic field is building up around the inductor.[1] After this field has been built up, the inductor allows current to flow through it normally. When the electricity supply is turned off, the magnetic field around the coil supports the flow of current for a brief interval, before the field disappears.
Inductance (L) (measured in henries) is an effect resulting from the magnetic field that forms around a current-carrying conductor that tends to resist changes in the current. Electric current through the conductor creates a magnetic flux proportional to the current. A change in this current creates a change in magnetic flux that, in turn, by Faraday's law generates an electromotive force (EMF) that acts to oppose this change in current. Inductance is a measure of the amount of EMF generated for a unit change in current. For example, an inductor with an inductance of 1 henry produces an EMF of 1 volt when the current through the inductor changes at the rate of 1 ampere per second.
The number of loops, the size of each loop, and the material it is wrapped around all affect the inductance. For example, the magnetic flux linking these turns can be increased by coiling the conductor around a material with a high permeability such as iron. This can increase the inductance by 2000 times, although less so at high frequencies.
An "ideal inductor" has inductance but no resistance or capacitance, and it does not dissipate energy. A real inductor has not only inductance but also some resistance (due to resistivity of the wire) and some capacitance. At some frequency, usually much higher than the working frequency, a real inductor behaves as a resonant circuit (due to its self capacitance). In addition to dissipating energy in the resistance of the wire, magnetic core inductors may dissipate energy in the core due to hysteresis, and at high currents may show other departures from ideal behavior due to nonlinearity.
Hydraulic analogy
The behavior of an inductor can be described by using a hydraulic analogy.[1] An inductor can be modeled by the flywheel effect of a heavy turbine rotated by the flow. When water (current) first starts to flow, the stationary turbine will cause an obstruction in the flow and high pressure (voltage) opposing the flow until it gets turning. Once it is turning, if there is a sudden interruption of water flow, the turbine will continue to turn by inertia, generating a high pressure to keep the flow moving. (Magnetic interactions in transformers are not modeled hydraulically.)
Applications
Inductors are used extensively in analog circuits and signal processing. Along with capacitors and other components, inductors are used to form tuned circuits that can emphasize or filter out specific signal frequencies. This can range from the use of large inductors as chokes in power supplies, which in conjunction with filter capacitors remove residual hum or other fluctuations from the direct current output, to such small inductances as generated by a ferrite bead or torus around a cable to prevent radio frequency interference from being transmitted down the wire. Smaller inductor/capacitor combinations provide tuned circuits used in radio reception and broadcasting, for instance.
Two (or more) inductors that have coupled magnetic flux form a transformer, which is a fundamental component of every electric utility power grid. The efficiency of a transformer may decrease as the frequency increases due to eddy currents in the core material and skin effect on the windings. Size of the core can be decreased at higher frequencies and, for this reason, aircraft use 400 hertz alternating current rather than the usual 50 or 60 hertz, greatly saving on weight through the use of smaller transformers.[2]
An inductor is used as the energy storage device in some switched-mode power supplies. The inductor is energized for a specific fraction of the regulator's switching frequency, and de-energized for the remainder of the cycle. This energy transfer ratio determines the input-voltage to output-voltage ratio. This XL is used in complement with an active semiconductor device to maintain very accurate voltage control.
Inductors are also employed in electrical transmission systems, where they are used to depress voltages from lightning strikes and to limit switching currents and fault current. In this field, they are more commonly referred to as reactors.
As inductors tend to be larger and heavier than other components, their use has been reduced in modern equipment; solid-state switching power supplies eliminate large transformers, for instance, and circuits are designed to use only small inductors, if any; larger values are simulated by use of gyrator circuits.
Inductor construction
An inductor is usually constructed as a coil of conducting material, typically copper wire, wrapped around a core either of air or of ferromagnetic material. Core materials with a higher permeability than air increase the magnetic field and confine it closely to the inductor, thereby increasing the inductance. Low frequency inductors are constructed like transformers, with cores of electrical steel laminated to prevent eddy currents. "Soft" ferrites are widely used for cores above audio frequencies, since they don't cause the large energy losses at high frequencies that ordinary iron alloys do. This is because of their narrow hysteresis curves, and their high resistivity prevents eddy currents. Inductors come in many shapes. Most are constructed as enamel coated wire wrapped around a ferrite bobbin with wire exposed on the outside, while some enclose the wire completely in ferrite and are called "shielded." Some inductors have an adjustable core, which enables changing of the inductance. Inductors used to block very high frequencies are sometimes made by stringing a ferrite cylinder or bead on a wire.
Small inductors can be etched directly onto a printed circuit board by laying out the trace in a spiral pattern. Some such planar inductors use a planar core.
Small value inductors can also be built on integrated circuits using the same processes that are used to make transistors. Aluminum interconnect is typically used, laid out in a spiral coil pattern. However, the small dimensions limit the inductance, and it is far more common to use a circuit called a "gyrator" which uses a capacitor and active components to behave similarly to an inductor.
Calculations for electric circuits
An inductor opposes changes in current. An ideal inductor would offer no resistance to a constant direct current; however, only superconducting inductors have truly zero electrical resistance.
In general, the relationship between the time-varying voltage v(t) across an inductor with inductance L and the time-varying current i'(t) passing through it is described by the differential equation:
When there is a sinusoidal alternating current (AC) through an inductor, a sinusoidal voltage is induced. The amplitude of the voltage is proportional to the product of the amplitude () of the current and the frequency (f) of the current.
In this situation, the phase of the current lags that of the voltage by 90 degrees. #
If an inductor is connected to a DC current source, with value I via a resistance, R, and then the current source short circuited, the differential relationship above shows that the current through the inductor will discharge with an exponential decay:
Laplace circuit analysis (s-domain)
When using the Laplace transform in circuit analysis, the transfer impedance of an ideal inductor with no initial current is represented in the s domain by:
-
- where
- L is the inductance, and
- s is the complex frequency
- where
If the inductor does have initial current, it can be represented by:
- adding a voltage source in series with the inductor, having the value:
(Note that the source should have a polarity that opposes the initial current)
- or by adding a current source in parallel with the inductor, having the value:
-
- where
- L is the inductance, and
- is the initial current in the inductor.
- where
Inductor networks
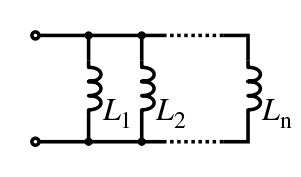
Inductors in a parallel configuration each have the same potential difference (voltage). To find their total equivalent inductance (Leq):
The current through inductors in series stays the same, but the voltage across each inductor can be different. The sum of the potential differences (voltage) is equal to the total voltage. To find their total inductance:
These simple relationships hold true only when there is no mutual coupling of magnetic fields between individual inductors.
Stored energy
The energy (measured in joules, in SI) stored by an inductor is equal to the amount of work required to establish the current through the inductor, and therefore the magnetic field. This is given by:
where L is inductance and I is the current through the inductor(****).
Q factor
An ideal inductor will be lossless, irrespective of the amount of current through the winding. However, typically inductors have winding resistance from the metal wire forming the coils. Since the winding resistance appears as a resistance in series with the inductor, it is often called the series resistance. The inductor's series resistance converts electrical current through the coils into heat, thus causing a loss of inductive quality. The quality factor (or Q) of an inductor is the ratio of its inductive reactance to its resistance at a given frequency, and is a measure of its efficiency. The higher the Q factor of the inductor, the closer it approaches the behavior of an ideal, loss less, inductor.
The Q factor of an inductor can be found through the following formula, where R is its internal electrical resistance and is capacitive or inductive reactance at resonance:
By using a ferromagnetic core, the inductance is greatly increased for the same amount of copper, multiplying up the Q. Cores however also introduce losses that increase with frequency. A grade of core material is chosen for best results for the frequency band. At VHF or higher frequencies an air core is likely to be used.
Inductors wound around a ferromagnetic core may saturate at high currents, causing a dramatic decrease in inductance (and Q). This phenomenon can be avoided by using a (physically larger) air core inductor. A well designed air core inductor may have a Q of several hundred.
An almost ideal inductor (Q approaching infinity) can be created by immersing a coil made from a superconducting alloy in liquid helium or liquid nitrogen. This supercools the wire, causing its winding resistance to disappear. Because a superconducting inductor is virtually lossless, it can store a large amount of electrical energy within the surrounding magnetic field (see superconducting magnetic energy storage).
Inductance formulae
The table below lists some common formulae for calculating the theoretical inductance of several inductor constructions.
| Construction | Formula | Dimensions |
|---|---|---|
| Cylindrical coil[3] |
| |
| Straight wire conductor |
| |
| ||
| Short air-core cylindrical coil |
| |
| Multilayer air-core coil |
| |
| Flat spiral air-core coil |
| |
| ||
| Toroidal core (circular cross-section) |
|
Synonyms
- Coil
- Choke (electronics)
- Reactor
See also
- Capacitor
- Electrical conductor
- Electricity
- Electronics
- Inductance
- Magnetic field
- Resistor
- Transformer
Notes
- ↑ 1.0 1.1 How Stuff Works, How Inductors Work. Retrieved February 23, 2009.
- ↑ Aspi Wadia, Aircraft electrical systems and why they operate at 400 Hz frequency. Retrieved February 23, 2009.
- ↑ 3.0 3.1 Hantaro Nagaoka, The Inductance Coefficients of Solenoids, Journal of the College of Science, Imperial University, Tokyo, Japan. 27:18. Retrieved February 23, 2009.
ReferencesISBN links support NWE through referral fees
- Giancoli, Douglas. 2007. Physics for Scientists and Engineers, with Modern Physics, 4th ed. Mastering Physics Series. Upper Saddle River, NJ: Prentice Hall. ISBN 978-0136139263.
- Gibilisco, Stan. 2005. Electricity Demystified. New York: McGraw-Hill. ISBN 0071439250.
- Hughes, Edward, et al. 2002. Electrical & Electronic Technology, 8th ed. Harlow: Prentice Hall. ISBN 058240519X.
- Tipler, Paul Allen, and Gene Mosca. 2004. Physics for Scientists and Engineers, Volume 2: Electricity and Magnetism, Light, Modern Physics, 5th ed. New York: W.H. Freeman. ISBN 0716708108
- Young, Hugh D., and Roger A. Freedman. 2003. Physics for Scientists and Engineers, 11th edition. San Francisco: Pearson. ISBN 080538684X.
External links
All links retrieved November 28, 2024.
- How Inductors Work. How Stuff Works.
- Coil Inductance Calculator. 66pacific.com.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.