Dendrite

Dendrite
Dendrite Soma Axon Nucleus Node of Ranvier Axon Terminal Schwann cell Myelin sheath
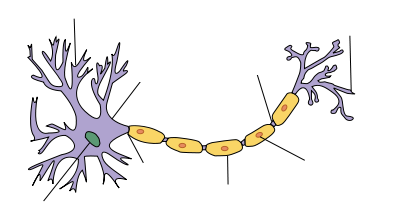
Structure of a typical neuron

Dendrite is a highly branched, generally tapering extension of a neuron (nerve cell) that typically receives signals from other neurons and transmits the signals toward the cell body (soma) from which the dendrite protrudes, normally using short-distance graded potentials rather than action potentials (nerve impulses). Although dendrites are where the majority of the input to the neuron occurs, in some cases dendrites may transmit signals from the cell body and release neurotransmitters to effect other neurons.

Most neurons have multiple dendrites, and commonly hundreds of twig-like dendrites that cluster near the cell body. The term dendrite comes from the Greek dendron (δένδρον), meaning "tree", and the overall shape and structure of a neuron's dendrites is called its dendritic tree. Dendritic branching is also called "dendritic arborization" and "dendritic ramification."

Dendrites are one of two types of protoplasmic protrusions that extend from a neuron cell body, the other being axons. An axon is a slender, armlike (not branched, except at its end) projection that extends from the cell body and typically conducts nerve impulses (action potentials) away from the cell body, causing at their terminal end the release of neurotransmitter into extracellular space, where they can excite or inhibit other neurons. However, in some sensory neurons, the nerve impulses travel along an axon from the periphery to the cell body, as with the typical dendrite function. (The historic distinction between axons and dendrites based on whether impulses travel toward or away from the cell body would classify this as a dendrite, but newer functional definitions based on whether there is a generation and transmission of a nerve impulse would classify this as an axon.) Axons have most of the same organelles as the dendrites and the cell body, but lack Golgi apparatus and Nissl bodies. Both differ from the soma in that they lack the cell nucleus.

From the development of the intricate branching pattern that is unique to each specific neuronal class, to the way they integrate the input from other neurons, to the way they convey stimulation, dendrites reflect a complex coordination at the cellular level. The unlocking of the mysteries of dendrite development and coordination offers the potential for important medical advances, including the adaptive immune response and cancer therapy immunotherapy.

The long outgrowths on immune system dendritic cells are also called dendrites. These dendrites do not process electrical signals.

Overview

A dendrite is a projection of a neuron. A neuron or nerve cell is a highly specialized, electrically excitable cell in the nervous system that conducts nerve impulses between different parts of the body. Neurons can process and transmit information from both internal and external environments, communicating this information via chemical or electronic impulse across a synapse (the junction between cells) and utilizing the action potential—an electrical signal that is generated by means of the electrically excitable membrane of the neuron. In vertebrate animals, neurons are the core components of the brain, spinal cord, and peripheral nerves.

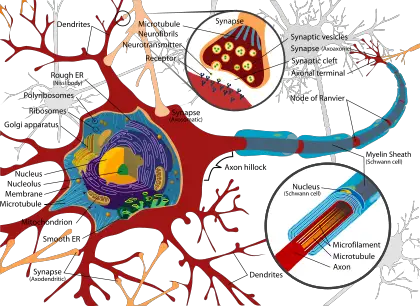
The three main structural regions of a typical neuron are: a soma, or cell body, which contains the nucleus; an axon, which carries an electric impulse; and one or more dendritic trees, which typically receive input. One can also separate out from the axon a region designated as the axon terminal, which refers to the small branches of the axon that form the synapses, or connections with other cells, and often functions to transmit signals to the other cells.

The soma or perikaryon is the bulbous end of a neuron, from which the dendrites and axon branch off. The soma contains many organelles; granules called Nissl granules; and the cell nucleus as the key feature.

The axon is one of the two types of protoplasmic protrusions extending from the neuron cell bodies. The axon is a slender, armlike projection that can extend tens, hundreds, or even tens of thousands of times the diameter of the soma in length and typically conducts electrical impulses away from the neuron's cell body. The function of the axon is to transmit information to different neurons, muscles, and glands. In certain sensory neurons (pseudounipolar neurons), such as those for touch and warmth, the electrical impulse travels along an axon from the periphery to the cell body, and from the cell body to the spinal cord along another branch of the same axon. No neuron ever has more than one axon. The axon is specialized for the conduction of the particular electric impulses known as action potentials.

Dendrites are the second of the two types of protoplasmic protrusions that extrude from the cell body of a neuron. These are cellular extensions with many branches and are specialized to receive chemical signals from the axon termini of other neurons. Dendrites convert these signals into small electric impulses and transmit them to the soma. Electrical stimulation is transmitted onto dendrites by upstream neurons (usually their axons) via synapses which are located at various points throughout the dendritic tree. Dendrites play a critical role in integrating these synaptic inputs and in determining the extent to which action potentials are produced by the neuron. Some recent research has suggested that dendrites can support action potentials and release neurotransmitters, a property that was originally believed to be specific to axons, although whether these processes should be considered dendrites or axons is also not firmly established based on differing definitions used for the terms (see below).

Dendrites are distinguished in general from axons by several features, including shape (dendrites often taper while axons usually maintain a constant radius), length (dendrites are restricted to a small region around the cell body while axons can be much longer), and function (dendrites usually receive signals while axons usually transmit them). All of these rules have exceptions, however. For example, while the axon and axon hillock are generally involved in information outflow, this region can also receive input from other neurons. Information outflow from dendrites to other neurons can also occur. And axons can be very short (and even absent) in some types of neurons. In the case of neurons without axons, the dendrites may serve the function of transmitting signals from the cell body. Both dendrites and axons tend to share the same organelles as the soma, although both lack the nucleus, and axons lack Golgi apparatus and Nissl bodies that are found in dendrites.

The distinction between dendrites and axons is not always clear. For example, neurons classified as unipolar (or pseudounipolar, since they originate as bipolar neurons) have one process that extends from the cell body and it forms two ends (a central process and a peripheral process, both with branches at their ends, where there are sensory endings/receptive terminals). These are chiefly sensory neurons of the peripheral nervous system. Some classify this extension as a dendrite, using the older definition of dendrites as processes that transmit impulses toward the cell body. However, functional definitions based on the generation and transmission of an impulse classify this as an axon (Marieb and Hoehn 2010).

The diffusely branching dendrites, of which there may be hundreds near the cell body in motor neurons, provide an extensive surface area for receiving signals from other neurons and transmitting them to the cell body. These signals are not usually action potentials, as is found in axons, but rather graded potentials. Some neuron types (bipolar) have a single fused dendrite (albeit with many branches at the end) in addition to one axon. But other neuron neuron types (multipolar) have many dendrites extending form the cell body.

Certain classes of dendrites (i.e. Purkinje cells of cerebellum, cerebral cortex) contain small projections referred to as "appendages" or "spines". Appendages increase receptive properties of dendrites to isolate signal specificity. Increased neural activity at spines increases their size and conduction which is thought to play a role in learning and memory formation. There are approximately 200,000 spines per cell, each of which serves as a postsynaptic process for individual presynaptic axons.

Electrical properties of dendrites

The structure and branching of a neuron's dendrites, as well as the availability and variation in voltage-gated ion conductances, strongly influences how the dendrite integrates the input from other neurons, particularly those that input only weakly. This integration is both "temporal"—involving the summation of stimuli that arrive in rapid succession—as well as "spatial"—entailing the aggregation of excitatory and inhibitory inputs from separate branches.

Dendrites were once believed to merely convey stimulation passively. In this example, voltage changes measured at the cell body result from activations of distal synapses propagating to the soma without the aid of voltage-gated ion channels. Passive cable theory describes how voltage changes at a particular location on a dendrite transmit this electrical signal through a system of converging dendrite segments of different diameters, lengths, and electrical properties. Based on passive cable theory one can track how changes in a neuron’s dendritic morphology changes the membrane voltage at the soma, and thus how variation in dendrite architectures affects the overall output characteristics of the neuron.

Although passive cable theory offers insights regarding input propagation along dendrite segments, it is important to remember that dendrite membranes are host to an abundance of proteins some of which may help amplify or attenuate synaptic input. Sodium, calcium, and potassium channels are all implicated in contributing to input modulation. It is possible that each of these ion species has a family of channel types each with its own biophysical characteristics relevant to synaptic input modulation. Such characteristics include the latency of channel opening, the electrical conductance of the ion pore, the activation voltage, and the activation duration. In this way, a weak input from a distal synapse can be amplified by sodium and calcium currents en route to the soma so that the effects of distal synapse are no less robust than those of a proximal synapse.

One important feature of dendrites, endowed by their active voltage gated conductances, is their ability to send action potentials back into the dendritic arbor. Known as backpropagating action potentials, these signals depolarize the dendritic arbor and provide a crucial component toward synapse modulation and long-term potentiation. Furthermore, a train of backpropagating action potentials artificially generated at the soma can induce a calcium action potential (a dendritic spike) at the dendritic initiation zone in certain types of neurons. Whether or not this mechanism is of physiological importance remains an open question.

Dendrite development

Despite the critical role that dendrites play in the computational tendencies of neurons, very little is known about the process by which dendrites orient themselves in vivo and are compelled to create the intricate branching pattern unique to each specific neuronal class. One theory on the mechanism of dendritic arbor development is the synaptotropic hypothesis. A balance between metabolic costs of dendritic elaboration and the need to cover receptive field presumably determine the size and shape of dendrites. It is likely that a complex array of extracellular and intracellular cues modulate dendrite development. Transcription factors, receptor-ligand interactions, various signaling pathways, local translational machinery, cytoskeletal elements, Golgi outposts, and endosomes have been identified as contributors to the organization of dendrites of individual neurons and the placement of these dendrites in the neuronal circuitry. For example, it was shown that β-actin zipcode binding protein 1 (ZBP1) regulates β-actin mRNA transport and translation in dendrites and contributes to proper dendritic branching (Perycz et al. 2011). Among the many extracellular signals (proteins/protein complexes) controlling the shape of dendritic arbor are AMPAR, NMDAR, CaSR, Semaphorin3a, Slit, Reelin, and Celsr-2, and Celsr-3, while among the many proteins identified as involved in intracellular processes underlying dendritic arborization are Ras, CAMKI, CREST, and SNAP-25(Urbanska et al. 2008).

References

ISBN links support NWE through referral fees

• Campbell, N. A., J. B. Reece, L. A. Urry, et al. 2008. Biology, 8th edition. San Francisco: Pearson/Benjamin Cummings. ISBN 9780805368444.

• Chamberlin, S. L., and B. Narins. 2005. The Gale Encyclopedia of Neurological Disorders. Detroit: Thomson Gale. ISBN 078769150X.

• Jan, Y. N, and L. Y. Jan. 2010. Branching out: Mechanisms of dendritic arborization. Nat Rev Neurosci. 11(6):449. Retrieved July 16, 2013.

• Kandel, E. R., J. H. Schwartz, and T. M. Jessell. 2000. Principles of Neural Science, 4th edition. New York: McGraw-Hill. ISBN 0838577016.

• Koch, C. 1999. Biophysics of Computation. Oxford: Oxford University Press. ISBN 0195104919.

• Marieb, E. N. and K. Hoehn. 2010. Human Anatomy & Physiology, 8th edition. Benjamin Cummings. ISBN 9780805395693.

• Perycz, M., A. S. Urbanska, P. S. Krawczyk, K. Parobczak, and J. Jaworski. 2011. Zipcode binding protein 1 regulates the development of dendritic arbors in hippocampal neurons. Journal of Neuroscience 31(14): 5271–5285. PMID 21471362. Retrieved July 15, 2013.

• Stuart, G., N. Spruston, and M. Hausser. 2008. Dendrites. Oxford: Oxford University Press. ISBN 0198566565.

• Urbanska, M., M. Blazejczyk, and J. Jaworski. 2008. Molecular basis of dendritic arborization. Acta neurobiologiae experimentalis 68(2): 264–288. PMID 18511961. Retrieved July 15, 2013.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Dendrite  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Dendrite"

Note: Some restrictions may apply to use of individual images which are separately licensed.