Archimedes
Archimedes (Greek: Ἀρχιμήδης) (c. 287 B.C.E. –212 B.C.E.) was an ancient Greek mathematician, physicist, engineer, astronomer, and philosopher, considered one of the greatest mathematicians in antiquity. Archimedes apparently studied mathematics in Alexandria, but lived most of his life in Syracuse. He discovered how to find the volume of a sphere and determined the value of Pi; developed a way of counting using zeros to represent powers of ten; discovered a formula to find the area under a curve and the amount of space enclosed by a curve; and may have been the first to use integral calculus. Archimedes also invented the field of statics, enunciated the law of the lever, the law of equilibrium of fluids, and the law of buoyancy. He was the first to identify the concept of center of gravity, and he found the centers of gravity of various geometric figures, including triangles, paraboloids, and hemispheres, assuming the uniform density of their interiors. Using only ancient Greek geometry, he also gave the equilibrium positions of floating sections of paraboloids as a function of their height, a feat that would be challenging for a modern physicist using calculus.
Archimedes only became widely known as a mathematician after Eutocius brought out editions of some of his works, with commentaries, in the sixth century C.E. Ancient writers were more interested in his inventions and in the ingenious war machines which he developed than in his achievements in mathematics. Plutarch recounts how Archimedes’ war machines defended Syracuse against Roman attackers during the Second Punic War. Many of Archimedes’ works were lost when the Library of Alexandria was burnt (twice), and survived only in Latin or Arabic translations.
Life
Archimedes was born in the seaport colony of Syracuse, Magna Graecia (now Sicily), around 287 B.C.E. He studied in Alexandria and then returned to Syracuse, where he spent the rest of his life. Much of what is known about Archimedes comes from the prefaces to his works and from stories related by Plutarch, Livy and other ancient historiographers. The preface to The Sand Reckoner tells us that Archimedes’ father, Phidias, was an astronomer. In the preface to On Spirals, Archimedes relates that he often sent his friends in Alexandria statements of his latest theorems, but without giving proofs. Some of the mathematicians there had claimed his results as their own, so Archimedes says that on the last occasion when he sent them theorems he included two which were false, “… so that those who claim to discover everything, but produce no proofs of the same, may be confuted as having pretended to discover the impossible.” He regarded Conon of Samos, one of the mathematicians at Alexandria, as a close friend and admired him for his abilities as a mathematician.
The dedication of The Sand Reckoner to Gelon, the son of King Hieron, is evidence that Archimedes was close to the family of King Hieron II. Plutarch’s biography of a Roman soldier, Marcellus, who captured Syracuse in 212 B.C.E., also tells us that Archimedes was related to King Hieron II of Syracuse. The same biography contends that Archimedes, possessing a lofty spirit and profound soul, refused to write any treatise on engineering or mechanics but preferred to devote himself to the study of pure geometry and pursued it without regard for food or personal hygiene.
And yet Archimedes possessed such a lofty spirit, so profound a soul, and such a wealth of scientific theory, that although his inventions had won for him a name and fame for superhuman sagacity, 4 he would not consent to leave behind him any treatise on this subject, but regarding the work of an engineer and every art that ministers to the needs of life as ignoble and vulgar, he devoted his earnest efforts only to those studies the subtlety and charm of which are not affected by the claims of necessity. These studies, he thought, are not to be compared with any others; in them the subject matter vies with the demonstration, the former supplying grandeur and beauty, the latter precision and surpassing power. 5 For it is not possible to find in geometry more profound and difficult questions treated in simpler and purer terms. Some attribute this success to his natural endowments; others think it due to excessive labour that everything he did seemed to have been performed without labour and with ease. For no one could by his own efforts discover the proof, and yet as soon as he learns it from him, he thinks he might have discovered it himself; so smooth and rapid is the path by which he leads one to the desired conclusion. 6 And therefore we may not disbelieve the stories told about him, how, under the lasting charm of some familiar and domestic Siren, he forgot even his food and neglected the care of his person; and how, when he was dragged by main force, as he often was, to the place for bathing and anointing his body, he would trace geometrical figures in the ashes, and draw lines with his finger in the oil with which his body was anointed, being possessed by a great delight, and in very truth a captive of the Muses. 7 And although he made many excellent discoveries, he is said to have asked his kinsmen and friends to place over the grave where he should be buried a cylinder enclosing a sphere, with an inscription giving the proportion by which the containing solid exceeds the contained. (Plutarch, Marcellus, 17: 3-7 translated by John Dryden)
Plutarch also gives three accounts of the death of Archimedes at the hands of the Roman soldiers. Although Marcellus ordered that Archimedes not be harmed, Roman soldiers came upon him at work and brutally murdered him. These stories seem designed to contrast the high-mindedness of the Greeks with the blunt insensitivity and brutality of the Roman soldiers.
4 But what most of all afflicted Marcellus was the death of Archimedes. For it chanced that he was by himself, working out some problem with the aid of a diagram, and having fixed his thoughts and his eyes as well upon the matter of his study, he was not aware of the incursion of the Romans or of the capture of the city. Suddenly a soldier came upon him and ordered him to go with him to Marcellus. This Archimedes refused to do until he had worked out his problem and established his demonstration, 5 whereupon the soldier flew into a passion, drew his sword, and dispatched him. Others, however, say that the Roman came upon him with drawn sword threatening to kill him at once, and that Archimedes, when he saw him, earnestly besought him to wait a little while, that he might not leave the result that he was seeking incomplete and without demonstration; but the soldier paid no heed to him and made an end of him. 6 There is also a third story, that as Archimedes was carrying to Marcellus some of his mathematical instruments, such as sun-dials and spheres and quadrants, by means of which he made the magnitude of the sun appreciable to the eye,b some soldiers fell in with him, and thinking that he was carrying gold in the box, slew him. However, it is generally agreed that Marcellus was afflicted at his death, and turned away from his slayer as from a polluted person, and sought out the kindred of Archimedes and paid them honour. (Plutarch, Marcellus, Chapter 19: 4-6, translated by John Dryden)
Thought and Works
Archimedes is considered by most historians of mathematics as one of the greatest mathematicians of all time. In creativity and insight, Archimedes exceeded any other European mathematician prior to the European Renaissance. Archimedes' works were not generally recognized, even in classical antiquity, though individual works were often quoted by three eminent mathematicians of Alexandria, Heron, Pappus and Theon, and only became widely known after Eutocius brought out editions of some of them, with commentaries, in the sixth century C.E. Many of Archimedes’ works were lost when the library of Alexandria was burnt (twice), and survived only in Latin or Arabic translations. The surviving works include On Plane Equilibriums (two books), Quadrature of the Parabola, On the Sphere and Cylinder (two books), On Spirals, On Conoids and Spheroids, On Floating Bodies (two books), Measurement of a Circle, and The Sand Reckoner. In the summer of 1906, J. L. Heiberg, professor of classical philology at the University of Copenhagen, discovered a tenth century manuscript which included Archimedes' work The Method, which provides a remarkable insight into how Archimedes made many of his discoveries.
Numerous references to Archimedes in the works of ancient writers are concerned more with Archimedes’ inventions, particularly those machines which were used as engines of war, than with his discoveries in mathematics.
Inventions
King Hiero II, who was rumored to be Archimedes' uncle, commissioned him to design and fabricate a new class of ships for his navy. Hiero II had promised large caches of grain to the Romans in the north in return for peace. Unable to deliver the promised amount, Hiero II commissioned Archimedes to develop a large, luxurious supply and war barge for his navy. The ship, coined Saracussia, after its nation, may be mythical. There is no record on foundry art, nor any other period pieces depicting its creation. It is solely substantiated by a description from Plato, who said "it was the grandest equation ever to sail."
Archimedes screw
It is said that the Archimedes Screw, a device which draws water up, was developed as a tool to remove bilge water from ships. Archimedes became well-known for his involvement in the defense of Syracuse, Italy against the Roman attack during the Second Punic War. In his biography of Marcellus, Plutarch describes how Archimedes held the Romans at bay with war machines of his own design, and was able to move a full-size ship complete with crew and cargo with a compound pulley by pulling a single rope.[1]
7And yet even Archimedes, who was a kinsman and friend of King Hiero, wrote to him that with any given force it was possible to move any given weight; and emboldened, as we are told, by the strength of his demonstration, he declared that, if there were another world, and he could go to it, he could move this. 8 Hiero was astonished, and begged him to put his proposition into execution, and show him some great weight moved by a slight force. Archimedes therefore fixed upon a three-masted merchantman of the royal fleet, which had been dragged ashore by the great labours of many men, and after putting on board many passengers and the customary freight, he seated himself at a distance from her, and without any great effort, but quietly setting in motion with his hand a system of compound pulleys, drew her towards him smoothly and evenly, as though she were gliding through the water. 9 Amazed at this, then, and comprehending the power of his art, the king persuaded Archimedes to prepare for him offensive and defensive engines to be used in every kind of siege warfare. These he had never used himself, because he spent the greater part of his life in freedom from war and amid the festal rites of peace; but at the present time his apparatus stood the Syracusans in good stead, and, with the apparatus, its fabricator. Plutarch, Chapter 14, Marcellus,7-9
Claw of Archimedes
One of his inventions used for military defense of Syracuse against the invading Romans was the “claw of Archimedes.” Archimedes also has been credited with improving accuracy, range and power of the catapult, and with the possible invention of the odometer during the First Punic War.
15 When, therefore, the Romans assaulted them by sea and land, the Syracusans were stricken dumb with terror; they thought that nothing could withstand so furious an onset by such forces. But Archimedes began to ply his engines, and shot against the land forces of the assailants all sorts of missiles and immense masses of stones, which came down with incredible din and speed; nothing whatever could ward off their weight, but they knocked down in heaps those who stood in their way, and threw their ranks into confusion. 2 At the same time huge beams were suddenly projected over the ships from the walls, which sank some of them with great weights plunging down from on high; others were seized at the prow by iron claws, or beaks like the beaks of cranes, drawn straight up into the air, and then plunged stern foremost into the depths, or were turned round and round by means of enginery within the city, and dashed upon the steep cliffs that jutted out beneath the wall of the city, with great destruction of the fighting men on board, who perished in the wrecks. 3 Frequently, too, a ship would be lifted out of the water into mid-air, whirled hither and thither as it hung there, a dreadful spectacle, until its crew had been thrown out and hurled in all directions, when it would fall empty upon the walls, or slip away from the clutch that had held it. As for the engine which Marcellus was bringing up on the bridge of ships, and which was called "sambuca" from some resemblance it had to the musical instrument of that name,25 4 while it was still some distance off in its approach to the wall, a stone of ten talents' weight26 was discharged at it, then a second and a third; some of these, falling upon it with great din and surge of wave, crushed the foundation of the engine, shattered its frame-work, and dislodged it from the platform, so that Marcellus, in perplexity, ordered his ships to sail back as fast as they could, and his land forces to retire.
5Then, in a council of war, it was decided to come up under the walls while it was still night, if they could; for the ropes which Archimedes used in his engines, since they imparted great impetus to the missiles cast, would, they thought, send them flying over their heads, but would be ineffective at close quarters, where there was no place for the cast. Archimedes, however, as it seemed, had long before prepared for such an emergency engines with a range adapted to any interval and missiles of short flight, and through many small and contiguous openings in the wall short-range engines called scorpions could be brought to bear on objects close at hand without being seen by the enemy. When, therefore, the Romans came up under the walls, thinking themselves unnoticed, once more they encountered a great storm of missiles; huge stones came tumbling down upon them almost perpendicularly, and the wall shot out arrows at them from every point; they therefore retired. 2 And here again, when they were some distance off, missiles darted forth and fell upon them as they were going away, and there was great slaughter among them; many of their ships, too, were dashed together, and they could not retaliate in any way upon their foes. For Archimedes had built most of his engines close p479behind the wall, and the Romans seemed to be fighting against the gods, now that countless mischiefs were poured out upon them from an invisible source.
17 However, Marcellus made his escape, and jesting with his own artificers and engineers, "Let us stop," said he, "fighting against this geometrical Briareus, who uses our ships like cups to ladle water from the sea, and has whipped and driven off in disgrace our sambuca, and with the many missiles which he shoots against us all at once, outdoes the hundred-handed monsters of mythology." 2 For in reality all the rest of the Syracusans were but a body for the designs of Archimedes, and his the one soul moving and managing everything; for all other weapons lay idle, and his alone were then employed by the city both in offence and defence. 3 At last the Romans became so fearful that, whenever they saw a bit of rope or a stick of timber projecting a little over the wall, "There it is," they cried, "Archimedes is training some engine upon us," and turned their backs and fled. Seeing this, Marcellus desisted from all fighting and assault, and thenceforth depended on a long siege. (Plutarch, Marcellus, Chapters 15 - 17
Death ray
It is said that Archimedes prevented one Roman attack on Syracuse by using a large array of mirrors (speculated to have been highly polished shields) to reflect concentrated sunlight onto the attacking ships, causing them to catch fire. This popular legend, dubbed the "Archimedes death ray," has been tested many times since the Renaissance and often discredited. It seems the ships would have had to be virtually motionless and very close to shore for them to ignite, an unlikely scenario during a battle. A group at Massachusetts Institute of Technology have performed their own tests and concluded that the mirror weapon was a possibility. [2], although later tests of their system showed it to be ineffective in conditions that more closely matched the described siege. The television show Mythbusters also took on the challenge of recreating the weapon and concluded that while it was possible to light a ship on fire, it would have to be stationary at a specified distance during the hottest part of a very bright, hot day, and would require several hundred troops carefully aiming mirrors while under attack. These unlikely conditions combined with the availability of other simpler methods, such as ballistae with flaming bolts, led the team to believe that the heat ray was far too impractical to be used, and probably just a myth.[3]
Archimedes' Principle
The story of Archimedes discovering buoyancy while sitting in his bathtub is described in Book 9 of De architectura by Vitruvius. King Hiero had given a goldsmith the exact amount of gold to make a sacred gold wreath. When Hiero received it, the wreath had the correct weight but the monarch suspected that some silver had been used instead of the gold. Since he could not prove it without destroying the wreath, he brought the problem to Archimedes. One day while considering the question, "the wise one" entered his bathtub and recognized that the amount of water that overflowed the tub was proportional to the amount of his body that was submerged. This observation is now known as Archimedes' Principle and gave him the means to measure the mass of the gold wreath. He was so excited that he ran naked through the streets of Syracuse shouting "Eureka! eureka!" (I have found it!). The dishonest goldsmith was brought to justice.
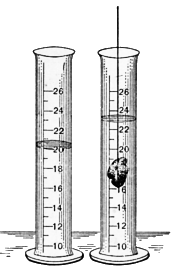 |
The Law of Buoyancy:
- The buoyant force is equal to the weight of the displaced fluid.
The weight of the displaced fluid is directly proportional to the volume of the displaced fluid (specifically if the surrounding fluid is of uniform density). Thus, among objects with equal masses, the one with greater volume has greater buoyancy.
Suppose a rock's weight is measured as 10 newtons when suspended by a string in a vacuum. Suppose that when the rock is lowered by the string into water, it displaces water of weight 3 newtons. The force it then exerts on the string from which it hangs will be 10 newtons minus the 3 newtons of buoyant force: 10 − 3 = 7 newtons.
The density of the immersed object relative to the density of the fluid is easily calculated without measuring any volumes:
Mathematics
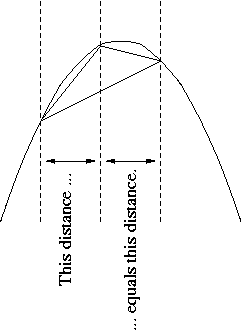
In creativity and insight, Archimedes exceeded any other European mathematician prior to the European Renaissance. In a civilization with an awkward numeral system and a language in which "a myriad" (literally "ten thousand") meant "infinity," he invented a positional numeral system and used it to write numbers up to 1064. He devised a heuristic method based on statistics to do private calculations that would be classified today as integral calculus, but then presented rigorous geometric proofs for his results. To what extent Archimedes’ version of integral calculus was correct is debatable. He proved that the ratio of a circle's circumference to its diameter is the same as the ratio of the circle's area to the square of the radius. He did not call this ratio Pi (π) but he gave a procedure to approximate it to arbitrary accuracy and gave an approximation of it as between 3 + 10/71 (approximately 3.1408) and 3 + 1/7 (approximately 3.1429). He was the first Greek mathematician to introduce mechanical curves (those traced by a moving point) as legitimate objects of study. He proved that the area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height. (See the illustration below. The "base" is any secant line, not necessarily orthogonal to the parabola's axis; "the same base" means the same "horizontal" component of the length of the base; "horizontal" means orthogonal to the axis. "Height" means the length of the segment parallel to the axis from the vertex to the base. The vertex must be so placed that the two horizontal distances mentioned in the illustration are equal.)
In the process, he calculated the earliest known example of a geometric progression summed to infinity with the ratio 1/4:
If the first term in this series is the area of the triangle in the illustration, then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines in the illustration, and so on. Archimedes also gave a quite different proof of nearly the same proposition by a method using infinitesimals (see "Archimedes' use of infinitesimals").
He proved that the ratio of the area of a sphere to the area of a circumscribed straight cylinder is the same as the ratio of the volume of the sphere to the volume of the circumscribed straight cylinder, an accomplishment which he had inscribed as his epitaph on his tombstone.[4]
Archimedes is probably also the first mathematical physicist on record, and the best until Galileo and Newton. He invented the field of statics, enunciated the law of the lever, the law of equilibrium of fluids, and the law of buoyancy. He was the first to identify the concept of center of gravity, and he found the centers of gravity of various geometric figures, including triangles, paraboloids, and hemispheres, assuming the uniform density of their interiors. Using only ancient Greek geometry, he also gave the equilibrium positions of floating sections of paraboloids as a function of their height, a feat that would be challenging for a modern physicist using calculus.
Astronomy
Archimedes was also an astronomer. Cicero writes that the Roman consul Marcellus brought two devices back to Rome from the ransacked city of Syracuse. One device mapped the sky on a sphere and the other predicted the motions of the sun and the moon and the planets (an orrery). He credits Thales and Eudoxus for constructing these devices. For some time the truth of this legend was in doubt, but the retrieval from an ancient shipwreck in 1902 of the Antikythera mechanism, a device dated to 150 – 100 b.c.e.. has confirmed the probability that Archimedes possessed and constructed such devices. Pappus of Alexandria writes that Archimedes had written a practical book on the construction of such spheres entitled On Sphere-Making.
Writings by Archimedes
- On the Equilibrium of Planes (2 volumes)
- This scroll explains the law of the lever and uses it to calculate the areas and centers of gravity of various geometric figures.
- On Spirals
- In this scroll, Archimedes defines what is now called Archimedes' spiral, the first mechanical curve (curve traced by a moving point) ever considered by a Greek mathematician.
- On the Sphere and the Cylinder
- In this scroll Archimedes proves that the relation of the area of a sphere to that of a circumscribed straight cylinder is the same as that of the volume of the sphere to the volume of the cylinder (exactly 2/3).
- On Conoids and Spheroids
- In this scroll Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids.
- On Floating Bodies (2 volumes)
- In the first part of this scroll, Archimedes spells out the law of equilibrium of fluids, and proves that water will adopt a spherical form around a center of gravity. This was probably an attempt at explaining the observation made by Greek astronomers that the Earth is round. His fluids were not self-gravitating: he assumed the existence of a point towards which all things fall and derived the spherical shape.
- In the second part, he calculated the equilibrium positions of sections of paraboloids. This was probably an idealization of the shapes of ships' hulls. Some of his sections float with the base under water and the summit above water, which is reminiscent of the way icebergs float.
- The Quadrature of the Parabola
- In this scroll, Archimedes calculates the area of a segment of a parabola (the figure delimited by a parabola and a secant line not necessarily perpendicular to the axis). The final answer is obtained by triangulating the area and summing the geometric series with ratio 1/4.
- Stomachion
- This is a Greek puzzle similar to a Tangram, and may be the first reference to this game. Archimedes calculates the areas of the various pieces. Recent discoveries indicate that Archimedes was attempting to determine how many ways the strips of paper could be assembled into the shape of a square. This is possibly the first use of combinatorics to solve a problem.
- Archimedes' Cattle Problem
- Archimedes wrote a letter to the scholars in the Library of Alexandria, who apparently had downplayed the importance of Archimedes' works. In this letter, he challenges them to count the numbers of cattle in the Herd of the Sun by solving a number of simultaneous Diophantine equations, some of them quadratic (in the more complicated version). This problem was recently solved with the aid of a computer. The solution is a very large number, approximately 7.760271 × 10206544 (See the external links to the Cattle Problem.)
- The Sand Reckoner
- In this scroll, Archimedes counts the number of grains of sand fitting inside the universe. This book mentions Aristarchus of Samos' theory of the solar system, concluding that it is impossible, and contemporary ideas about the size of the Earth and the distance between various celestial bodies.
- The Method
- This work, which was unknown in the Middle Ages, but the importance of which was realized after its discovery, pioneers the use of infinitesimals, showing how breaking up a figure into an infinite number of infinitely small parts could be used to determine its area or volume. Archimedes probably considered these methods not mathematically precise, and he used these methods to find at least some of the areas or volumes he sought, and then used the more traditional method of exhaustion to prove them.
Notes
- ↑ Ship Shaking Device, Syracuse, 214 B.C.E. by Kristin Shutts and Anne-Sinclair Beauchamp.[1]. e-museum, Smith College. Retrieved June 6, 2008.
- ↑ "Archimedes Death Ray" Experiment Results.MIT.
- ↑ "Mythbusters" Discovery Channel.Episode 55: Steam Cannon/Breakfast Cereal.Retrieved June 6, 2008.
- ↑ Tomb of Archimedes Sources.[2]. NYU Math Dept.Retrieved June 6, 2008.
ReferencesISBN links support NWE through referral fees
- Archimedes; Sir Thomas Heath, (Translator). The Works of Archimedes. reprint ed. Dover Publications 2002. ISBN 0486420841
- Archimedes; Reviel Netz. The Works of Archimedes: Translation and Commentary. Cambridge University Press, 2004. ISBN 0521661609
- Dijksterhuis, E. J. Archimedes. Princeton, Princeton Univ. Press, 1987. ISBN 0691084211.
- Kliner, Fred S.; Mamiya, Kliner Christin J. . "Gardener's Art Through the Ages," twelfth ed. Vol II. Los Angeles: Thompson Wadsworth, 2005.
- Laubenbacher, Reinhard, and David Pengelley. Mathematical Expeditions: Chronicles by the Explorers. 1999. ISBN 0387984348
- Plutarch. Plutarch's Lives, translated by John Dryden. New York: Modern Library, ASIN: B000RS0LX6
- Stadter, Philip A. Plutarch's historical methods: An analysis of the Mulierum virtutes. Harvard University Press, 1965. ASIN: B0007DKTAG
Introduction for young adults
- Benkick, Jeanne. Archimedes and the Door to Science. Bethlehem Books, 1995. ISBN 1883937124
- Zannos, Susan. The Life and Times of Archimedes. (Biography from Ancient Civilizations) Mitchell Lane Publishers, 2004. ISBN 1584152427
External links
All links retrieved August 12, 2023.
- Archimedes' Book of Lemmas at cut-the-knot
- Inside the Archimedes Palimpsest NOVA
- Archimedes' Cattle Problem
- Project Gutenberg, Archimedes, e-text
- Angle Trisection by Archimedes of Syracuse (Java)
- Archimedes'Triangle (Java)
- An ancient extra-geometric proof
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.